Rike hat ihre Bachelorarbeit mit dem Konzept über ihr Spiel im hyperbolischen Raum abgeschlossen. Heute war ihr Kolloquium. Grund zum Feiern. Sie hat in das Loft eingeladen. Rikes Mutter hat Kartoffel- und Nudelsalat gemacht, im Hof wurden Würstchen und 'was Vegetarisches gegrillt, das Wetter hat mitgespielt. Es gab zuerst Sekt, dann Bier und Wein – und den ganzen Abend Musikvideos. Als Max und Rike Crawling von Linkin Park sehen und Chester Bennington
Confusing what is real
singt, denken sie an Chester und überlegen, sich an der One More Light Fundation zu beteiligen. Dann erinnert sich Rike, was sie sich über die rellen Zahlen überlegt hatte. Es wäre sehr confusing.
Max Was meinst Du?
Definition reeller Zahlen
Rike Ich habe – so wie Du bei den natürlichen Zahlen – versucht, eine Definition für die reellen Zahlen zu finden. Im Algebra-Buch haben sie den Begriff des Körpers erklärt und auf ein Analysis-Buch verwiesen, in den Analysis-Büchern gibt es den Begriff des Körpers nicht. Und bei Wiki steht auch keine stringente Definition. Schau mal, hier steht unter der Überschrift Axiomatische Näherung: Wenn 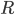
Max Hahahaha! Die Mathematiker tun sich schwer, ihre Zahlen zu definieren! Und wie geht es weiter?
Addition und Multiplikation
Rike Ich nehme jetzt mal die von Zorich: Man nimmt eine Menge (von Zahlen) und stattet sie mit der Addition und Multiplikation aus. Zum Beispiel soll es eine 0 geben, die wir zu jedem Element dazu addieren könnnen und das Ausgangselement erhalten:
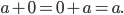
Und eine 1 für die Multiplikation:
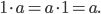
Max Okay, das ist doch klar.
Rike Dann gibt es ein paar vernünftige Forderungen für dies Rechenoperationen einzeln und zusammen, das Transitivitätsgesetz, das Distributivgesetz...
Max Okay.
Ordnung
Rike Außerdem fordert man, dass die reellen Zahlen in einer Linie angeordnet werden können, dass es ein Kleiner, Größer oder Gleich gibt.



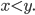
Max Okay, ist doch klar.
Rike Und dass sich diese Ordnung mit der Addition und Multiplikation verträgt.
Das Vollständigkeitsaxiom
Max Okay, und was ist nun confusing?
Rike Als letztes und wichtigstes Axiom, was nämlich die reellen Zahlen von den rationalen unterscheidet, gibt es das Vollständigkeitsaxiom. Das sagt – mal einfach ausgedrückt – dass für beliebige Zahlen
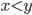
sich stets eine weitere finden lässt, c, die echt zwischen beiden steht:
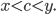
Max Okay, was ist das Problem?
Rike Das Problem ist, dass das nicht konstruktiv ist.

Die reellen Zahlen enthalten sozusagen die Grenzwerte von Folgen, aber wenn ich so eine Zahl ausrechnen will, z.B. mal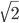
Max Hmm, 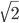
Rike Das ist eine Näherung! Wenn Du die quadrierst, kommt … warte, 1,99936 raus.
Max' trickreiche Skalierung
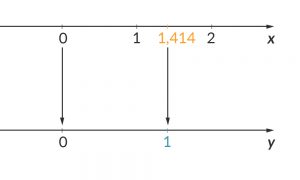
Max Stimmt! Dann haben die reellen Zahlen ein paar real confusing ones. Wer hat sich denn den Namen relle Zahlen ausgedacht? Ist ja total confusing! Also, dann mache ich mal einen Vorschlag: Ich definiere die reellen Zahlen so:
Bei
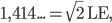
Du weißt schon, da schreibe ich "1" dran! Dann ist das Problem weg!

Rike Haha, meine reellen Zahlen sind die mit der oberen Skala, und ich kann die beiden aufeinander abbilden:
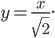
Wir können uns gegenseitig verständigen, wenn ich 1 LE habe, hast Du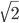
Max Rike, berechne das heute Abend bitte nicht ...
***
Übungsaufgaben
- Finde Formulierungen für das Transitivitätsgesetz und
- das Distributivgesetz!
- Gibt es noch andere Formulierungen für das Vollständigkeitsaxiom?
Lösungen
- Transitivitätsgesetz der Ordnung:
Für
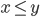
und
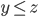
folgt
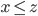
- Distributivgesetz:
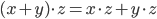
- Ja, zum Beispiel: Jede nichtleere, beschränkte Menge reller Zahlen
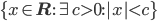
hat eine kleinste obere Schranke, das Supremum.