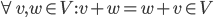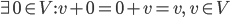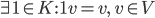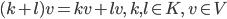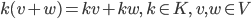Vektorraum im Supermarkt

Max hat Mira mit zu Rike gebracht. Ihm ist Mira im Supermarkt aufgefallen. Sie bediente an der Kasse und konnte die Summe von Max' Einkauf im Kopf addieren.

Max Hi, Rike, heute habe ich Mira mitgebracht! Sie hat im Supermarkt alle Rekorde gebrochen.

Rike Hi, Mira.

Mira Hi!

Rike Mira, stimmt das?

Mira Ja, Ich habe in Kalkutta Angewandte Mathe studiert, aber ich konnte es nicht zuende bringen. Meine Familie ist nach Deutschland gegangen.

Rike Und wie machst Du das im Supermarkt?

Mira Das ist nicht schwer. Ich kann mir die Preise gut merken, wie jede andere Kassiererin. Bei Max' Einkauf waren viele Artikel mehrfach, und die Preise multipliziere ich einfach mit der Anzahl. Aber noch viel mehr Spass macht so eine Inventur, da kann ich ein ganzes Regal überblicken.

Rike Hey, Du bist ja ein echtes Mathetalent! Wie machst Du das?

Artikel als Vektoren

Mira Ach, ich stelle mir alles im mehrdimensionalen Raum vor. Für jeden Artikel habe ich einen Vektor.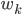

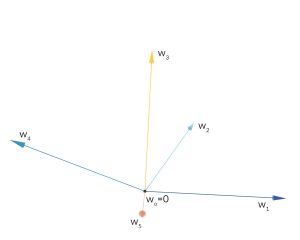
An der Kasse kommen bei einem Einkauf immer Mehrfache von den Vektoren an:

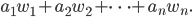
Das ist dann ein Einkauf.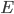

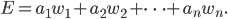
Im Regal stehen ebenso mehrere gleiche Artikel, ich nehm' jetzt mal das Summenzeichen:

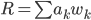
und der gesamte Supermarkt hat Waren

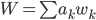
Also,

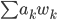
beschreibt immer eine Warenmenge.

Rike Sieht aus wie ein Vektorraum.

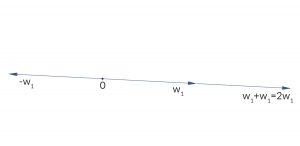
Addition von Vektoren

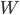
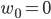
Mira Ja, hat mich an die Lineare-Algebra-Vorlesung erinnert. Wir können im Raum aller Waren Waren hinzunehmen und wegnehmen.

ist der Nullvektor, er steht für keine Ware.

Max Ok, der Nullvektor, geht jemand in den Supermarkt und kauft nichts!

Mira Haha, ich brauche das in meiner Welt. In Kalkutta haben wir Vektorräume über reellen oder komplexen Zahlen behandelt.

Max Was heißt das?

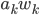
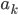
Mira Es sind Vielfache erlaubt, und ist reell oder komplex.

Max Also 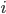mal ein Bier? Ein komplexes Bier?

Mira Siehst Du, das geht nicht, ich mache das anders.

Rike Stimmt, für den Vektorraum brauchst Du Koeffizienten aus einem Körper. Vorallem brauchst Du das für die lineare Unabhängigkeit.

Lineare Unabhängigkeit von Vektoren

Max Was ist das schon wieder?

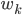
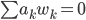
Rike Die Vektoren wären linear abhängig, wenn Du aus verschiedenen Artikeln den Nullvektor erzeugen kannst:

und nicht alle .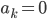

Max Das ist doch klar!

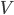
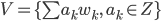
Mira Ja! Für meinen “Vektorraum” lasse ich nur ganze Koeffizienten zu:

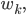
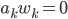
Trotzdem habe ich viele Eigenschaften des normalen Vektorraumes, sogar die lineare Unabhängigkeit der Vektoren und aus

folgt entweder

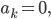
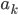
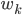
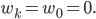
weil die Koeffizienten ganz sind oder ist der Nullvektor:

Max Klar, der Nulleinkauf besteht entweder aus kein Mal Zartbitter-Schokolade oder gar kein Artikel!

Preise als lineares Funktional

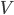
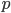
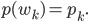
Mira Und außerdem habe ich den Raum umgebaut. Ihr wisst ja, jeder Artikel hat einen Preis :

Der Preis eines Einkaufs berechnet sich

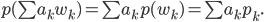
Rike Mein Gott, das ist ja ein lineares Funktional!

Mira Stimmt, es ist sogar eine Art Maß, die Artikelpreise sind selbstverständlich nichtnegativ und rational. Weil wir weniger Preise als Artikel haben, der höchste Preis ist 999,- €, habe ich die Artikel mit demselben Preis zusammengefasst.

Äquivalenzrelation

Rike Aaah, eine Äquivalenzrelation.

Mira Stimmt, ich sage

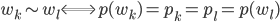
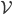
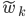
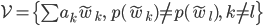
Zwei Artikel sind äquivalent, wenn sie denselben Preis haben. Und dann bilde ich den Raum der Waren mit unterschiedlichen Preisen:

Max Dann hast Du ja die Artikel mit ihrem Preis identifiziert, dann ist der Darjeeling Tee für 1,99 € dasselbe wie Schweizer Schokolade?

Mira Haha, an der Kasse schon!

***

Übungsaufgaben

1. Was ist ein Vektorraum?
2. Ist Miras Realtion eine Äquivalenzrelation?

Lösungen

1. Ein Vektorraum wird über einem Körper definiert. Zunächst sollen die Elemente von , die Vektoren, addierbar sein. Die Addition erfüllt die folgenden Eigenschaften:

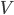
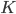
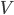
   Außerdem gibt es eine Art Vielfaches: Für und soll
   existieren und
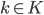
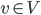
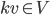
2. Ja, die Relation ist reflexiv, symmetrisch und transitiv