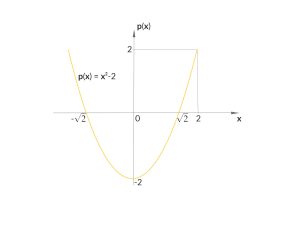
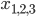Jule, Rikes Schwester, kommt am Wochenende mal wieder ins Lipperland und hat einen Kuchen mitgebracht. Jule hat ihr Abitur bestanden, sie hat an einer renommierten Uni angefangen, Angewandte Informatik zu studieren, sie hat inzwischen ihr erstes objektorientiertes Programm geschrieben und ein bisschen Algebra und Prädikatenlogik gehört. Aber sie weiß nicht, wie man konkrete Zahlen berechnet.
Jule Hi, Rike, ich wollte Dich gerne mal hier besuchen! Wie geht es Dir, was macht Dein Spiel?
Rike Hi, Jule, schön , dass Du kommst. Das Spiel geht voran, für die erste Etappe habe ich eine Finanzierung, ich könnte noch Mitstreiter gebrauchen. Aber wie geht es Dir? Wie gefällt es Dir im Ruhrpott?
Jule Der Einstieg war echt schwierig. Ich musste auf einmal in Anweisungen denken und Fehler suchen – in Programmen, die ich selbst geschrieben habe und die doch so simpel waren, aber einfach nicht laufen wollten......
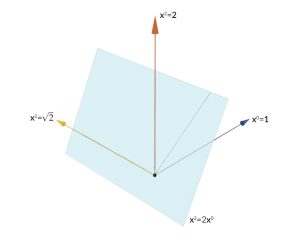
Rike Hmmm, kommt mir bekannt vor. Ich habe neulich mit Max über reelle Zahlen diskutiert, und festgestellt, dass wir am Ende immer nur rationale Zahlen darstellen. Schon bei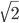
Jule Berechnen heißt ja, endlich viele Anweisungen ausführen...
Rike Ja, stimmt, man braucht eine Vorschrift und soll nur endlich viele Anweisungen auszuführen. Ich habe da neulich einen interessanten algebraischen Zugang gelesen:
Jule Erzähl!
Vektorräume
Rike Kennst doch Vektorräume? Das sind Räume 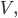
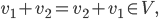
wo es den Nullvektor 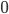
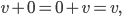
und das Negative 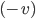
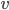
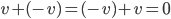
Jule Klar, eben Vektoren, kenne ich im 3-Dimensionalen.
Rike Ja, und jetzt nehmen wir noch Vielfache zu und lassen rationale Faktoren zu:
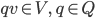
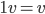
und noch ein paar Distributivgesetze.
Jule Ok. Und weiter?
Rike Die Vorstellung mit den 3-dimensionalen Vektoren musst Du jetzt vergessen.
Jule Ja?
Lineare Abhängigkeit
Rike Ja, wir schreiben erst mal die Gleichung für lineare Abhängigkeit von 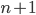
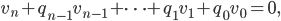
und die 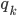
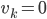
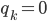
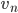

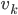
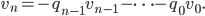
Ein Vektorraum für Zahlen
Jule Okay. Was hat das jetzt mit Zahlen zu tun?
Rike Nehmen wir mal
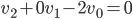
Jule Okay, dann ist 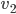
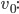
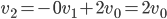
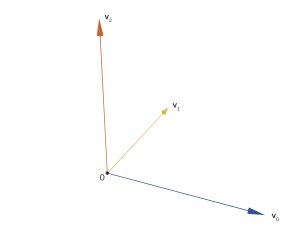
Rike Stimmt. Und wenn Du jetzt die Vektoren 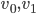
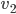
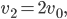
dass 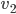
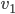
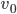
Jule Okay.
Rike Und jetzt verlassen wir diese Vektorenvorstellung wirklich, also diese Pfeile und Richtungen, wir setzen für 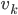
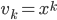
Jule Was, 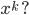
Rike Gute Frage, das ist die 
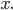
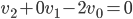
wird dann
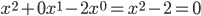
Jule Und weiter?
Rike Jetzt haben wir die Eigenschaft, dass 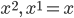
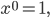
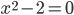
erfüllen, linear abhängig sind. Und dieses ist ihre Gleichung.
Jule Jetzt müssen wir die nur noch lösen, klar
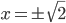
sind die Lösungen.
Rike Ja, wir setzen den "Vektor"
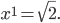
Und
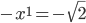
ist natürlich linear abhängig von 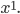
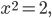
und
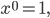
also
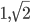
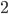
sind linear abhängig.
Berechnung von Nullstellen von Polynomen
Jule Naja, nicht schlecht, aber mit dem Berechnen bin ich noch nicht viel weiter.
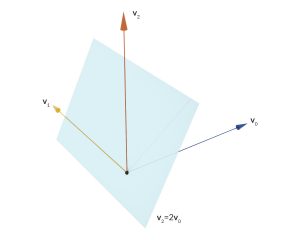
Rike Richtig, wir bestimmen einfach die Nullstellen von
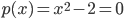
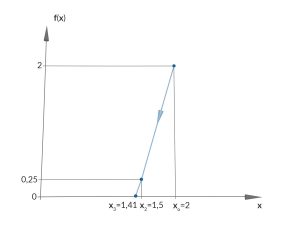
Nehmen wir mal das Newton-Verfahren, dann hätten wir mit 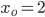
Algebraische Zahlen
Jule Dann hast Du jetzt vorgeschlagen, Zahlen 
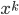
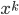
Rike Hey Jule, Du hast gerade algebraische Zahlen verstanden! Haben wir noch mehr Kuchen?
Jule Klar!
Rike Super, später muss ich Dir noch die Rolle der 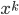
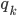
***
Übungsaufgabe
Nenne weitere Beispiele algebraischer Zahlen!
Lösung
Das sind alle möglichen Lösungen von
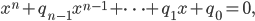
mit
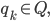
also zum Beispiel
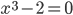
Das hat offensichtlich die Lösung
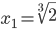
Wenn wir nun
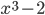
durch
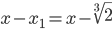
teilen, erhalten wir
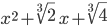
Dafür benutzen wir die p-q-Formel. Leider ist die Diskriminante
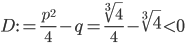
So bekommen wir zwei weitere komplexe Wurzeln
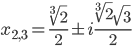
.