Musterbildung bei algebraischen Zahlen

Rike fährt dieses Wochenende zu ihrer Schwester Jule nach Duisburg. Sie besuchen den Landschaftspark Duisburg-Nord. Bei Einbruch der Dunkelheit wird er beleuchtet. Er erinnert Rike an ein Bild von algebraischen Zahlen. Sie zeigt es Jule auf dem Smartphone.

Rike Hier, schau, hier ist ein Bild von algebraischen Zahlen, sieht aus wie die Duisburger Kulisse.

Algebraische Zahlen

Jule Achja, algebraische Zahlen, Du nimmst ein Polynom mit rationalen Koeffizienten

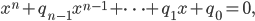
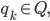
und die Nullstellen sind algebraische Zahlen. Sie bilden einen linearen Raum und sind linear abhängig, wenn man die Potenzen als Variablen versteht. Du wolltest mir noch erklären, was mit den und ist.

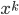
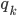
Rike Ja, machen wir. Du weisst ja noch, dass die Koeffizienten 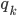rational sind.

Jule Warum eigentlich?

Rike Naja, die rationalen Zahlen bilden einen Körper und lassen sich gut durch Rechner darstellen, sie sind Quotienten ganzer Zahlen.

Jule Okay. Und sag, da hat jemand algebraische Zahlen numerisch berechnet?

Rike Ja, Stephen Brooks hat ein Programm geschrieben, mit dem er eben diese Polynome

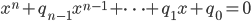
erzeugt. Und dann berechnet er die Lösungen. Lass uns mal ein recht einfaches Polynom nehmen:

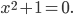
Jule Hmm. Das hat komplexe Lösungen, hatten wir gerade im Studium:

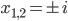
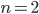
Der Fundamentalsatz der Algebra

Rike Stimmt, dann verstehst Du, dass so ein Polynom -ten Grades komplexe Lösungen hat.

Jule Okay.

Rike Lass uns nun

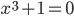
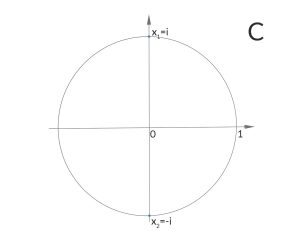
nehmen. Um die Gleichung zu lösen, hilft die eulersche Formel weiter, wir schreiben für eine komplexe Zahl

Eulersche Formel

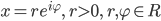
n-te Wurzeln aus -1

Die -ten Wurzeln sind dann

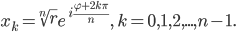
Bei uns, mit

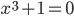
haben wir

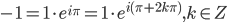
und folglich

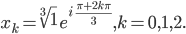
Das ergibt

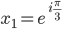
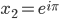
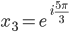
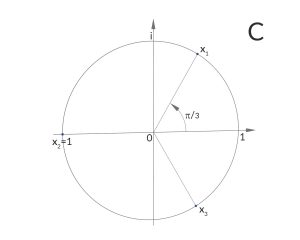
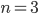
Jule Stimmt!

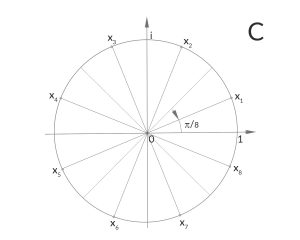
Rike Und so weiter. Für die 4. Wurzel aus -1 erhalten wir folgendes Bild:

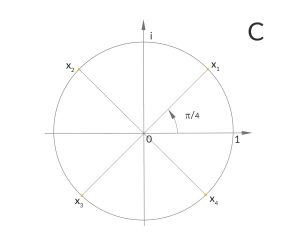
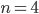
Jule Cool!

Rike Stephen Brooks hat Polynome bis zum 8. Grad zugelassen, und

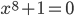
hat die Lösungen:

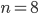
Jule Das sind nur Mustergleichungen, wenn wir jetzt einen freien Parameter zulassen, zum Beispiel

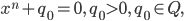
dann kriegen wir

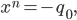
so eine Art Skalierung für die Lösung.

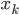
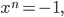
Rike Richtig, die Lösungen dieser Gleichung sind dieselben wie die für

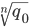
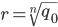
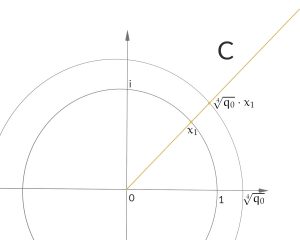
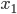
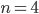
nur ein Skalierungsfaktor: . Die Lösungen liegen alle auf dem Kreis mit dem Radius

Das sind abzählbar unendlich viele, ja 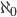viele.

Jule Verstehe, füllen die nicht die Geraden nahezu aus?

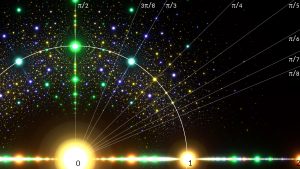
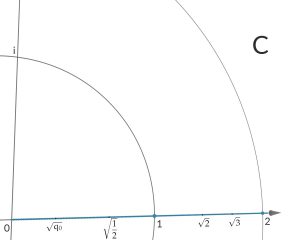
Rike Ja, sie füllen die fast überall aus. Die Kreis- und Richtungsstruktur mit den Winkeln

0°, 22,5°, 25,71°, 30°, 36°, 45°, 60°, 90°

ist ganz klar zu sehen.

Reelle Lösungen

Dann gibt es noch Gleichungen mit garantierten reellen Lösungen:

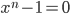
Jule Ja, klar, 1 und -1 sind Lösungen.

Rike Wenn wir die wieder “skalieren”, also

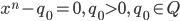
betrachten, dann haben wir schon mal

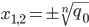
als reelle Lösungen. Diese algebraischen Zahlen liegen auf der reellen Achse und füllen sie fast aus.

Jule Aber wie hat dieser Stephen die Wurzeln berechnet? Wir konnten das nicht. Gibt es noch einen Trick?

Rike Schau mal, der Code für sein Programm ist veröffentlicht. Natürlich rechnet er nur mit Näherungen, also mit rationalen Zahlen.

Jule Dann sind diese Punkte hier in seinem Bild gar keine algebraischen Zahlen?

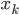
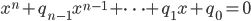
Rike Nein, die meisten sind komplexe Zahlen mit rationalen Real- und Imaginärteil, die näherungsweise

lösen.

Jule Müsste nicht die ganz Ebene dicht ausgefüllt sein? Am Rand wird es dünner?

Rike Ja, Du hast recht, er geht bis zum 8. Grad bei den Polynomen und hat nicht alle Skalierungen zugelassen, er hat, wart mal, hier stehts,

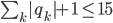
gefordert.

Jule Okay, sieht trotzdem schön aus!

***

Übungsaufgabe

Gibt es in Brookes Bild auch "echte" algebraische Zahlen?

Lösung

Ja, i, 0, 1, 2 und alle anderen rationalen Zahlen, weil auch Polynome 1. Grades zugelassen sind.