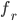Die Rendergleichung

Max kommt zu Rike ins Loft. Er hat ein Glas mitgebracht und stellt es auf den Tisch. Max ist mit seinem Studium ein bisschen weiter und belegt nun Computergrafik.

Max Hi, Rike, wie geht es Dir?

Rike Hi, Max! Gut! Und selbst?

Max Danke! Ich habe hier ein Glas mitgebracht. Sieht doch ganz einfach aus. Das will ich modellieren, eine Glastextur drauflegen und rendern. Aber ich bekomme es nicht so richtig hin! Woran liegt das?

Rike Oh, Max, das ist ein weites Feld, da steckt ziemlich viel Mathematik dahinter. Ich versuche mal, das zu erklären.

Max Okay.

Lokales Lichtsetting

Rike Wir fangen mal mit nicht transparenten, nicht selbstleuchtenden Oberflächen an. Nehmen wir mal an, Dein Glas ist aus weißer Keramik. Dann müssen wir für jeden Punktder Oberfläche des Glases – oder besser des Bechers – ausrechnen, wie viel Licht er in Richtungzu einem Pixel der virtuellen Kamera abgibt.

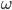
Max Trifft denn nur ein Lichtstrahl auf meine Kamera?

Rike Hey Max, gute Frage, einer wäre etwas wenig. Jeder Pixel auf dem Sensor der virtuellen Kamera erhält einen anderen Strahl, der vonausgeht.

Max Okay, das sind bei einer Vollformatkamera ca.:

px px,

echt 'ne Menge Pixel!

Tangenten und Normale

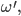
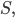
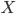
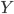
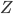
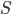
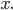
Rike Stimmt. Die Berechnungen muss man für jedes Pixel machen. Dann haben wir noch eine Lichtquelle in Richtung vom Punkt aus gesehen. liegt auf der Oberfläche da legen wir die Tangenten und an, zeigt in die Richtung der Normalen von in

Max Mein Glas ist aber rund! Nicht so, wie Du gezeichnet hast!

Rike Das macht nichts, hier, das ist so:

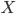
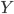
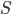
Du musst Dir das ganz lokal vorstellen! Statt der Krümmung nehmen wir die Tangentialebene, lokal!

Die Bidirectional Reflection Distribution Function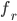

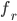
Max Und was ist am Rand des Bechers? Wie legst Du da die Tangenten?

Rike Hey Max, noch eine gute Frage! Wir müssen natürlich nicht nur lokal schauen, sondern die Oberflächen aller Objekte der Szene betrachten, also auch die Ränder. Am Rand des Bechers ändert sich die Reflexionseigenschaft. Entweder ist da Luft oder der Tisch unterm Becher. Das wird durch eine Funktion beschrieben,

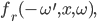
die heißt Bidirectional Reflection Distribution Function.

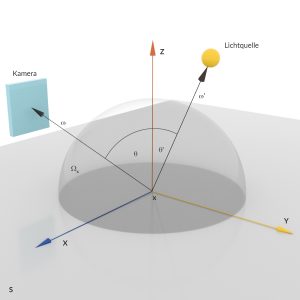
Max Hmm, BRDF? Hab ich schon mal im 3D-Programm gesehen.

Rike Richtig, an der Stelle kannst Du die Reflexionseigenschaft der einzelnen Objekte einstellen, also richtungsabhängige Reflexion oder Rauigkeit. Aus all den Oberflächeneigenschaften der einzelnen Objekte und der Geometrie Deiner Szene errechnet der Renderer des 3D-Programms diese Funktion 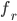für jeden Punkt.

Max Okay, was noch?

Der Energieerhaltungssatz

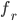
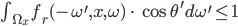
Rike Diese Funktion muss eine Bedingung erfüllen:

Max Was ist das?

Rike Die Formel steht für die Energieerhaltung im Lokalen. Sie sagt, dass in einer kleinen Umgebung von weniger Licht reflektiert als einfällt. Der Rest wird in Wärme umgewandelt.

Max Na klar! Was ist ?

Rike ist der Winkel zwischen der Richtung und der Normalen. beschreibt die Projektion in -Richtung, also das Licht, was von der Oberfläche reflektiert wird.

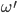
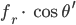
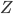
Max Okay, verstehe.

Die Hitfunction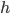

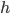
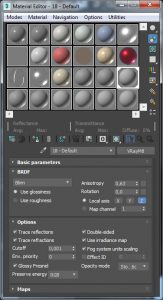
Rike Jetzt brauchen wir noch eine Größe

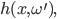
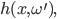
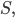
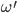
das ist die Hitfunction. Sie beschreibt den ersten Punkt auf der Oberflächeden ein Strahl von der Lichtquelle in Richtung gehend trifft, eben hit.

Max Wozu brauche ich den?

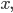
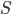
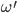
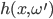
Rike Der emmitiert Licht in Richtung der Punkt ist dann bei Verdeckungen der Oberflächedie neue Position einer Lichtquelle in-Richtung. Beim Becher braucht man das wirklich.

Max Okay. Jetzt haben wir immer noch keine Gleichung.

Rike Stimmt. Als Letztes brauchen wir noch den Begriff der Lichtintensität

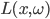
für ein kleines Flächenelement umfür jede Richtung

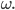
Max Und wie geht das mit der Farbe? Brauche ich nicht für jeden Punkt die RGB-Werte?

Rike Ja klar, Du kannst das für jeden Kanal einzeln ausrechnen, wenn Du willst, sogar für jede Wellenlänge des Lichtes. In der finalen Gleichung kommt die Lichtintensität (pro Kanal oder Wellenlänge)

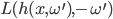
vor, das ist die Lichtintensität am Hitpunkt in negativer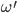-Richtung.

Max Klar!

Die Rendergleichung für nicht transparente, nicht selbstleuchtende Objekte

Rike So, jetzt haben wirs. Die Rendergleichung für nicht selbstleuchtende, nicht transparente Objekte ist

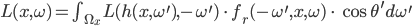
Max Oooh!

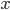
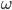
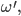
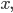
Rike Das ist die grundlegende Gleichung für die Lichtintensität. Sie besagt, dass die Lichtintensität an einem Punkt in Richtungdurch das Integral der Lichtintensitäten der Hitpunkte vonüber alle Richtungenprojiziert auf die Normalenrichtung der Oberfläche anbestimmt wird.

Max Sag mal, die Lichtintensität inberechnet sich durch das Integral über alle Lichtintensitäten am Hitpunkt? Wie geht das?

Rike Da liegt wirklich der Hase im Pfeffer! Das Integral ist keine Berechnungsvorschrift. Es ist eine Gleichung über die physikalischen Zusammenhänge, die eine starke Abhängigkeit des Lichtes in einem Punkt von seinem Umgebungslicht beschreibt.

Max Stimmt.

Rike Die Rendergleichung ist eine Integralgleichung. Es gibt nur sehr wenige explizite Lösungen.

Max War alles umsonst?

Rike Nein, die Gleichung ist wunderbar! Sie ist seit 1986 bekannt und es gelingt immer besser, sie anzuwenden und zu lösen, auch für Dein Glas kriegen wir das hin. Die besten Renderer von 3D-Programmen lösen das sehr trickreich. Fahr doch mal zur FMX, da wird das toll erklärt. Du kannst auch wiederkommen, dann machen wir weiter. Für heute reicht's Dir wohl. Willst Du ein Glas Wein?

***

Übungsaufgaben

1. Nenne triviale Lösungen der Rendergleichung!
2. Ist die Funktionin unserem Becher-auf-dem-Tisch-Beispiel stetig und/oder differenzierbar?

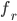
Lösungen

1. 1. ~ absolutes Dunkel
   2. ~ ein flächiges Licht, senkrecht über der Ebene
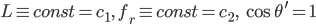
2. Nein, ist nur stückweise stetig und differenzierbar.