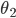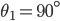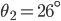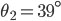Reflexion und Brechung

Max kommt wieder zu Rike ins Loft. Er hat dasselbe Glas wieder mitgebracht. Er will nun endlich sein Textur- und Renderingproblem lösen.

Max Hi, Rike, wollen wir heute weiter machen? Ich will das mit dem Glas wirklich verstehen und gut aussehen lassen.

Rike Hi, Max!

Max Mein Rendering sieht so aus! Das Glas ist ganz durchsichtig. Gilt denn da die Rendergleichung nicht?

Rike Doch, Du hast Dein Glas gerendert und es sieht so aus, als hättest Du nur die Transparenz und Reflexionen beachtet, hier diese weißen Flecken sind wohl die Spiegelungen Deiner viereckigen Lampe?

Max Hmmm.

Die Rendergleichung für nicht transparente Objekte

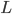
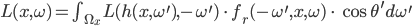
Rike Die Rendergleichung, die wir letztens besprochen haben, galt für nicht transparente und nicht selbstleuchtende Objekte. Wir hatten die Lichtintensität in einem Punkt mittels

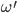
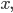
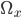
berechnet. Wir hatten über alle Lichtstrahlen einer Lichtquelle für die die Halbkugel treffen, integriert.

Die Rendergleichung für transparente Objekte

Bei transparenten Materialien ist das anders. Lass uns – nur so zum Verständnis – eine transparente Box auf diese graue Oberfläche 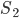legen.

Max Okay, dann geht das Licht da hindurch, stimmts?

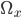
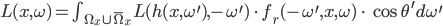
Rike Stimmt. Es geht hindurch bis zur nicht transparenten Oberfläche und wird dort reflektiert. Die Rendergleichung geht jetzt über die obere Halbkugel und den Teil der unteren Halbkugel der im Transparenten liegt. Die Bidirectional Reflection Distribution Function beschreibt nun die Geometrie der Szene, die Reflexions- und Brechungseigenschaften. Sie ist jetzt aufwändiger zu berechnen.

Max Okay, aber irgendwas hat bei mir nicht geklappt. Wurde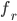 falsch berechnet?

Rike Ooooh, das glaube ich nicht, Ihr habt doch an der Uni die besten Renderer. Schau mal, hier. Dein Glas hat eine sehr glatte Oberfläche. Die Reflexion hast Du gut simuliert.

Max Aber es sieht nicht echt aus.

Rike Stimmt, wenn wir versuchen, hindurch zu sehen, dann geht das nur in der Mitte, am Rand sieht alles verzerrt aus und durch den Boden kann man fast nichts erkennen, wie bei einer komischen Lupe. Aber wenn Du von oben durchsiehst, in das leere Glas hinein, dann ist das kein Problem.

Max Okay. Das wollte ich ja gerade simulieren.

Das snelliussche Brechungsgesetz

Rike Da steckt das snelliussche Brechungsgesetz drin, Lichtstrahlen werden so gebrochen:

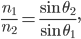
für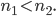

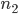
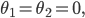
Das Material mit dem größeren Brechungsindex heißt optisch dichter. Wenn Du senkrecht durchschaust, ist

also keine Brechung. Du musst also bei Deiner Simulation nur die Zahlen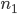 und angeben, bei Glas ist das ca. 1.6 und Luft hat ca. 1.0. Wenn Du einen Laserpointer dabei hast, können wir sogar selbst bestimmen, wenn wir die Winkel messen.

Max Naja.

Rike Bei recht dünnen Gläsern, thin, wie Fensterscheiben oder Displays vermeidet man technisch die Brechung, bei der Simulation kann man sie auch weglassen ...

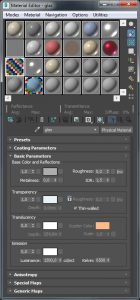
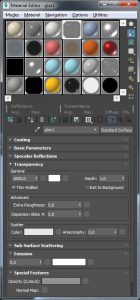
Max Hmmm, ich dachte, das Glas ist ja dünn!

Rike Hey, dann deaktiviere doch diesen Button THIN-WALLED.

Übrigens könnten wir mit dem Laserpointer auch den Zuckergehalt von Flüssigkeiten bestimmen.

Max Auch den Alkoholgehalt?

Rike Hahaha!

***

Übungsaufgaben

1. Berechne für !
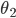
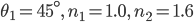
2. Das snelliussche Brechungsgesetz gilt auch für den Übergang von optisch dickeren zu dünneren Materialien. Berechne wie bei 1. den kritischen Winkel, für den wird!

Lösungen