Max kommt zu Rike ins Loft. Er hat das Glas erneut mitgebracht. Max hat es 3D-modelliert und eine schöne Textur draufgelegt und gerendert. Jetzt will er unbedingt ein weihnachtliches, künstlerisches Bild vor Schwarz haben, aber es klappt nicht. Seine Fotos von dem Glas bleiben schwarz, sein Rendering sieht unrealistisch aus. Nun fragt er Rike um Rat.
Max Hi, Rike, wie geht es Dir?
Rike Hi, Max, bald Weihnachten? Ich freue mich, endlich mal wieder bei meiner Familie zu sein. Bisschen freie Zeit, Zeit für neue Ideen...
Max Ich habe hier wieder das Glas. Mit Videokameras kenne ich mich gut aus, aber solche transparente Sachen! Es lässt sich nicht real und nicht virtuell fotografieren, immer bleibt das Bild dunkel. Ich finde Transparenz ziemlich unpraktisch!
Rike Hey, Max, das kriegen wir hin! Zuerst fotografieren wir es. Mit Fotoapparat und Licht. Das Licht muß auf das Glas fallen, damit es schöne Reflexionen und Brechungen gibt. Im Dunkeln macht das keinen Spaß.
Max Richtig!
Rike Im Virtuellen mußt Du ebenfalls Licht benutzen und auf das Glas richten. Dann gibt es verschiedene Möglichkeiten der Ansicht. Zum Beispiel kannst Du eine Kamera wählen, die eine parallele Perspektive hat. Dann sind die Projektionen auf die Kamera recht einfach. Parallele Linien des Glases bleiben parallel, rechte Winkel bleiben bei der Abbildung unverändert.
Max Ok, ist ja klar.
Rike Stimmt. Wir empfinden aber das fotografierte Bild als natürlich. Da haben wir eine Zentralperspektive zur Kamera hin. Die CG-Leute haben sich geeinigt und in die Mitte der Kamera den Nullpunkt gesetzt. In Richtung der “Welt” geht die positive z-Richtung. Außerdem brauchen wir noch eine Fläche für den Kamerasensor. Wenn Du dann renderst, musst Du angeben, wie groß Dein Bild wird, dann wird diese Fläche in die Pixel zerlegt, die Du brauchst, also diskretisiert. Das Rendering berechnet dann für jeden Pixel, was darauf abgebildet wird.
Camera Space
Zuerst braucht man aber geeignete Koordinaten im 3D-Raum: Du hast hier oft mit Strahlen zu tun, die zur Kamera hin gehen. Deshalb wurde der sogenannte Camera Space gefunden:
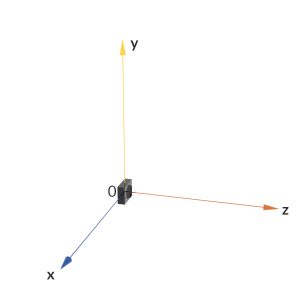
Hier wird gern ein linkshändiges Korrdinatensystem verwendet. Die Kamera liegt im Koordinatenursprung 

Homogene Koordinaten
Wegen der vielen Strahlen werden die Koordinaten gern so geschrieben:

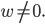
Max Ach, 4-dimensional?
Rike Das sieht nur so aus, 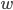
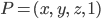
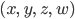
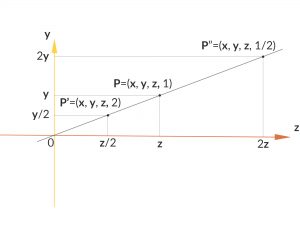
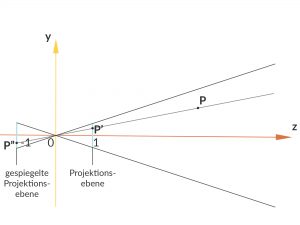
Orthographische Kamera
Max Ok, ist ja praktisch.
Rike Mit diesen homogenen Korrdinaten geht die parallele Projektion recht einfach:
Ein Punkt 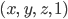
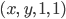

Max Was, nur die 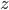
Rike Ja, das ist schon alles.
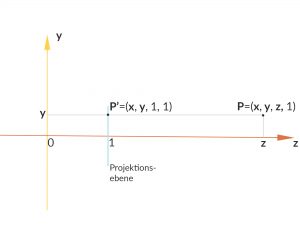
Perspektivische Kamera
Bei der perspektivischen Kamera hat man einen Öffnungswinkel 


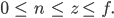
Max Ja, das macht Sinn, im Nahbereich braucht man ein Makroobjektiv und bildet anders ab.
Rike Okay, wenn man also festlegt, wie nah und wie fern die Kamera abbildet, dann ist die Abbildung linear und kann mit einer 4 x 4-Matrix geschrieben werden:
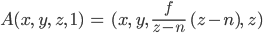
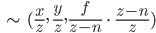
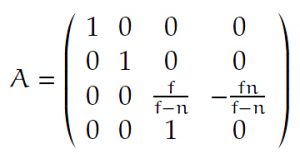
Max Hmmm, warum wird das nicht auf 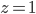
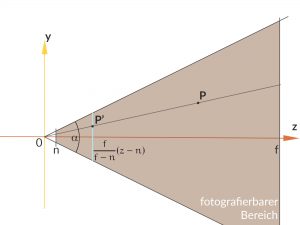
Rike In dem Physically Based Rendering-Modell lässt man einen Nahbereich zu. Das heißt, dass die Kamera zwar im Nullpunkt sitzt, aber erst ab

fotografiert. Wie im echten Leben, die Objektive funktionieren noch nicht ganz nah an der Kamera. Wenn Du
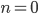
setzt, bekommst Du
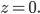
Max Okay, weißt Du auch, wie die virtuellen Kameras im Nahbereich, also bei
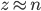
funktionieren? Ist das auch linear? Es sieht immer alles so rund aus?
Fisheye
Rike Beim Fisheye zum Beispiel, da wird hauptsächlich im Nahbereich gerechnet, jeder Punkt 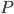

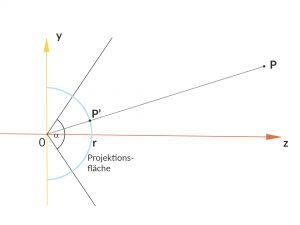
Auch das ist nicht schwer:
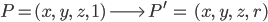
Das kann man auch mit einer Matrix schreiben:
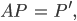
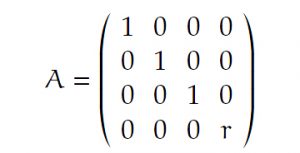
Max Okay, verstehe. Das gibt immer kreisförmige Bilder.
Rike Stimmt.
Max Jetzt lass uns das mal rendern. Sag mal, kann ich denn nicht wie eine Fliege mit einer virtuellen Kamera in das Glas hineinfliegen und von innen nach draußen schaun?
Rike Ja klar! Eine Fliege hat einen weiten Blickwinkel, aus Linien werden Kurven...


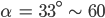 mm-Objektiv.
mm-Objektiv.

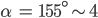 mm-Objektiv.
mm-Objektiv.***
Übungsaufgaben
- Wie sieht die Matrix für die orthogonale Projektion im Camera Space mit homogenen Koordinaten aus?
- Ist die Abbildung linear?
Lösungen
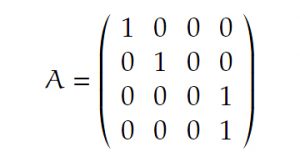
- Ja
