Letzte Nacht hatte Rike einen Alptraum: Sie geht auf einem Grat in einem riesigen Gebirge, rechts und links ganz tiefe Schluchten. Dann fällt sie zu der einen Seite und wacht auf. Sie macht sich Sorgen, sie hat Liebeskummer. Sie hat gehört, dass sich Max in Lila verliebt hat. Jetzt überlegt sie, ob sie nach Kalkutta fliegen soll, um mit Max ein paar schöne Tage zu verbringen. Doch wenn sie zu Max fliegt, wird Ben ihr das übelnehmen. Sie hat das Gefühl, sich endgültig einer Seite zuwenden zu müssen, sich somit entscheiden zu müssen.
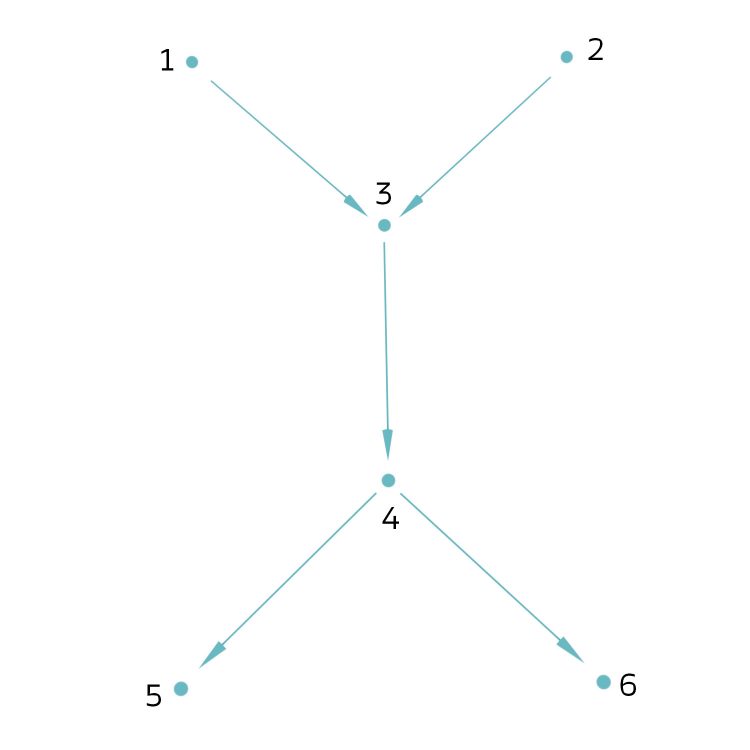
Jetzt nimmt sie ein Blatt Papier und schreibt die Beziehungssituation graphisch auf. Wenn zwei Menschen zusammenkommen, sich lieben und sich trennen, sieht das graphisch so aus:
Beziehungsgraphen
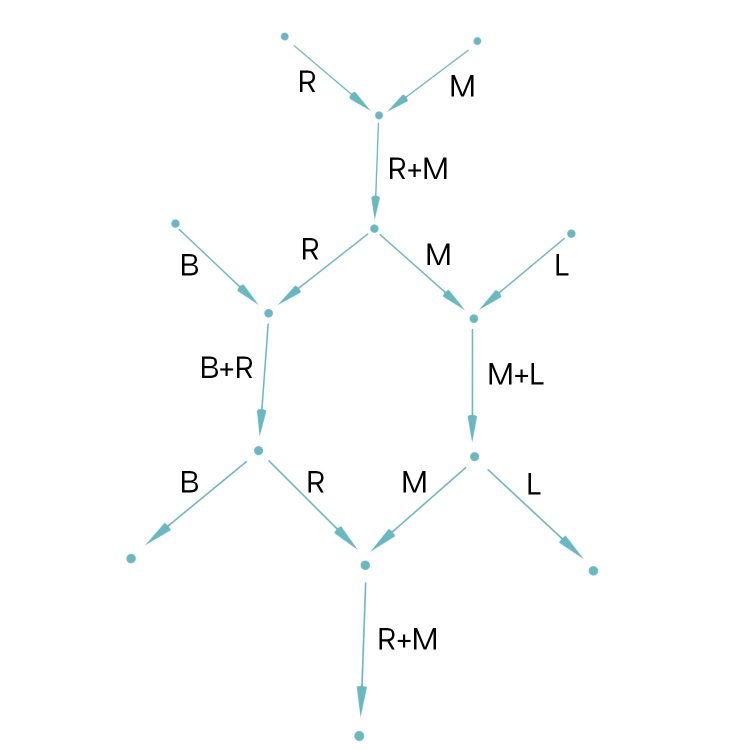
Doch bei ihr ist es komplizierter, es sind nicht nur 2 Menschen, sondern 4. Sie hat Max vor langer Zeit getroffen und ist seine Freundin. Dann sind Ben und Lila dazugekommen. Jetzt ist sie mit Ben zusammen, und Max mit Lila. Wenn sie nach Kalkutta fliegt, vielleicht kommt sie dann wieder mit Max zusammen?
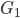
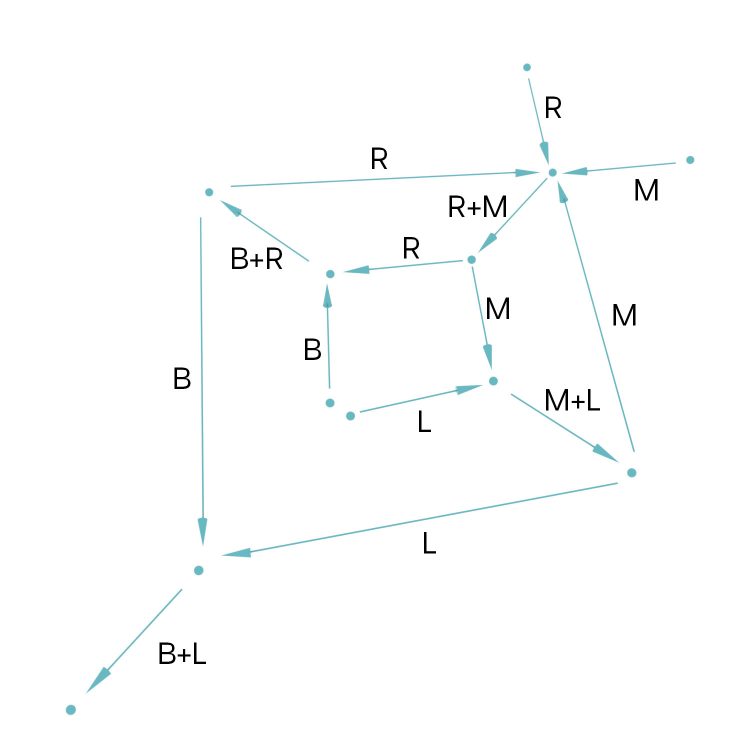
Neben der Traurigkeit über Max‘ neue Liebe hat sie auch Hoffnung. Hm, ein schöner planarer Graph, denkt sie. Doch was passiert, wenn sie mit Ben nach Kalkutta fliegt, mit Max wieder zusammenkommt und wenn Ben sich in Lila verliebt? Dann braucht sie eine weitere Dimension, um das zu zeichnen:
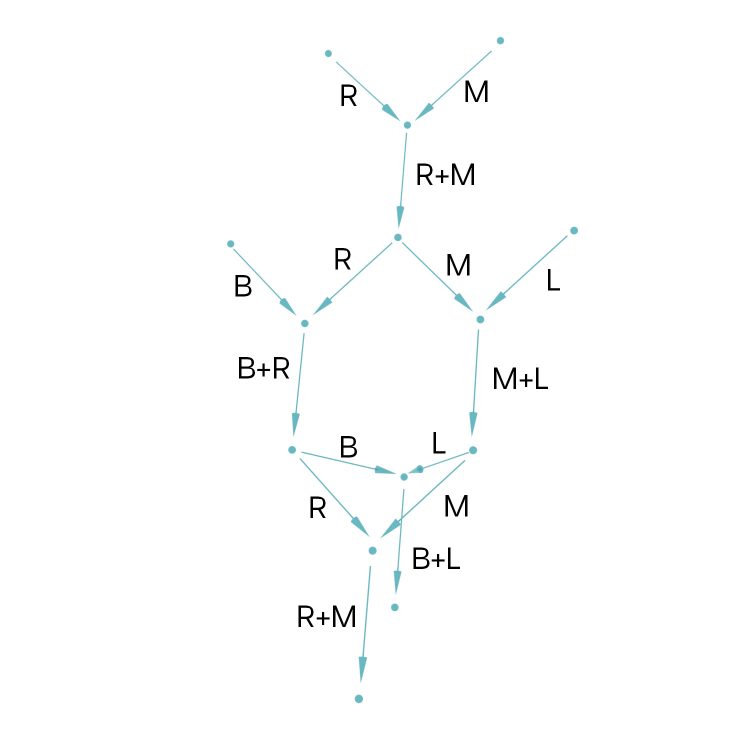
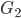
Jetzt ist der Graph nicht mehr planar, sie weiß nicht weiter. Hier in Bielefeld weiß niemand weiter. Da muss sie wohl ihre Freundin Anna in Berlin anrufen.
Rike Hi, Anna. Ich habe so einen verdammten Graphen, der ist nicht planar. Warte, ich schicke ihn Dir. Hier! Weißt Du, welche Eigenschaften er hat? Wie kann ich ihn zeichnen?
Satz von Kuratowski
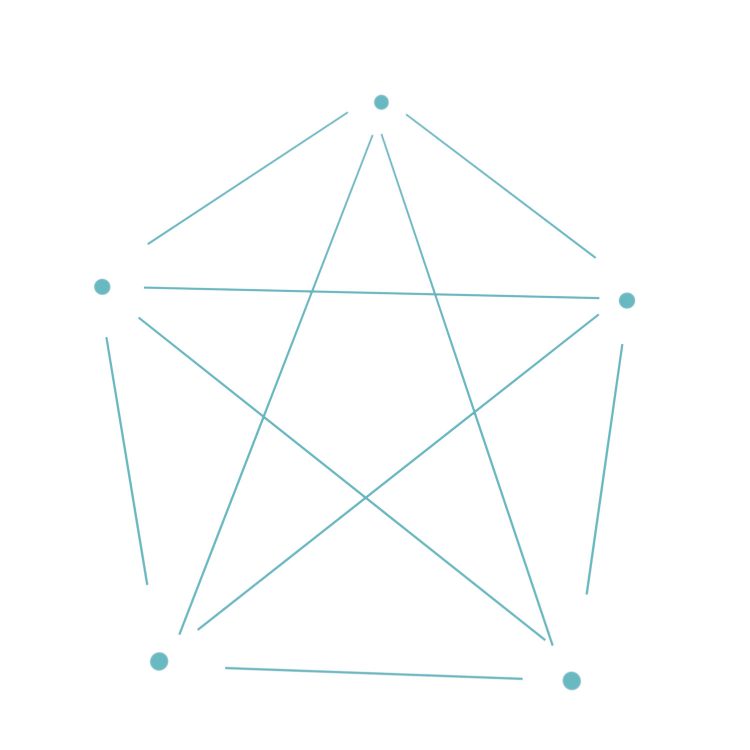
Anna Hi, Rike, geht es Dir nicht so gut? Ich versuche es mal. Wenn der Graph wirklich nicht planar ist, dann muss er entweder den Graphen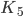 
oder den 
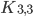enthalten. Der eine ist ein vollständiger Graph mit 5 Vertices, der andere ist ein zweigeteilter, vollständiger, sogenannter bipartiter. Das ist der Satz von Kuratowski.
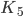
Rike Oh, ich glaube, die beiden sind nicht drin.
Anna Kannst Du nicht einen von den beiden nach unten gehenden Teilen nach oben klappen?
Rike Stimmt, ich wollte den Graphen zeichnen wie im Phasenraum, der Pfeil dachte ich, repräsentiert die Zeit und geht immer nach unten.
Anna Nein, das brauchst Du nicht. Ein Graph ist kein Phasenraum. Die Vertices sind nicht die Zustände.
Rike Stimmt, bei mir sind die Edges die Zustände und die Vertices stehen für Zustandsänderungen. Dann klappe ich einen Zweig nach oben, und fertig ist der planare Graph über die 4er Beziehung.
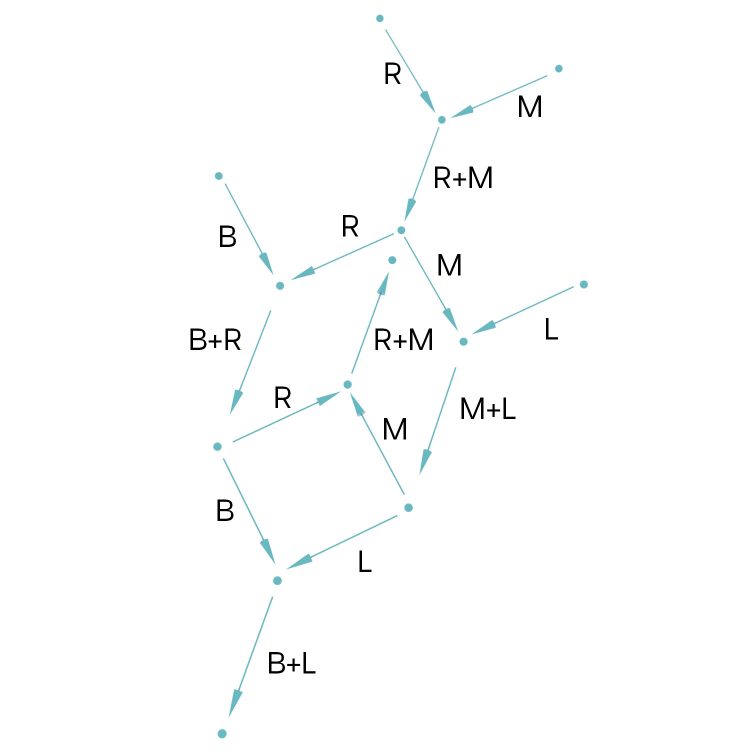
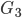
Euler-Charakteristik
Anna Hast Du schon die Euler-Charakteristik bestimmt?
Rike Wie geht das? Ich dachte, die gibt’s nur für Polyeder?
Anna Nein, die gibt’s auch für Graphen. Man schneidet so einen Polyeder an einer Kante auf, klappt ihn auf und interpretiert die Vertices und Edges als die eines Graphen. Bei der Zählung der Flächen nimmt man noch die äußere dazu. Die Euler-Charakteristik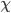 
ist eine Invariante für jeden Graphen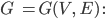 
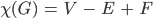
V … Anzahl der Vertices/Knoten
E … Anzahl der Edges/Kanten
F … Anzahl der Faces/Flächen inklusive die äußere
Jeder planare, zusammenhängende Graph hat die Charakteristik 2.
Rike Okay, bei diesem Graphen 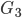ist
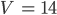
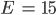
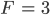
und folglich
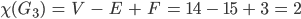
Die Euler-Charakteristik stimmt. Das ist einfach schön.
Anna Kann ich noch was für Dich tun?
Rike Danke, das war‘s erstmal. Grüß David von mir!
***
Übungsaufgaben
- Beweise die Euler-Charakteristik.
- Wie ändert sich der Graph 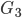, wenn man die beiden Kanten R+M identifiziert und versucht, den neuen Graphen
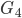planar zu zeichnen?
Lösung
- Mit vollständiger Induktion über die Anzahl der Vertices V.
