Hyperbolische Geometrie für Serververbindungen II

Ben und Rike hatten den hyperbolischen Abstand im Einstein-Modell für Computernetze diskutiert. Jetzt will Ben mit Rike die Netze selbst diskutieren. Das Modell ist nicht so einfach zu verstehen und vor lauter Modellbetrachtungen kommt Ben nicht auf den Punkt. Sein Ziel ist es, selbst so ein Netz aufzubauen und vorher zu simulieren

Ben Dank Dir, Rike, habe ich diesen hyperbolischen Abstand als Formel einigermaßen verstanden, dieses

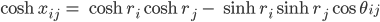
x_ij ist der hyperbolische Abstand des Vertex V_i zum Vertex V_j
r_i bzw. r_jsind deren Abstände eines Vertex V_i bzw. V_j zum Nullpunkt
θ_ij ist der Winkel zwischen den Strecken 0V_i und 0V_j

Bens kleines Einstein-Netz

Jetzt will ich das auf das Einstein-Modell anwenden. Ich will so ein Netz aufbauen. Lass uns doch mal ein nichttriviales Beispiel nehmen. Ich würde ein paar Server innen verteilen, sagen wir mal 4 Stück und außen die restlichen. Jeder „innere“ Server ist mit 8 äußeren verbunden, jeder innere Server mit jedem anderen inneren, und jeder äußere Server ist mit 2 inneren Servern verbunden und mit jedem direkten inneren Nachbarn.

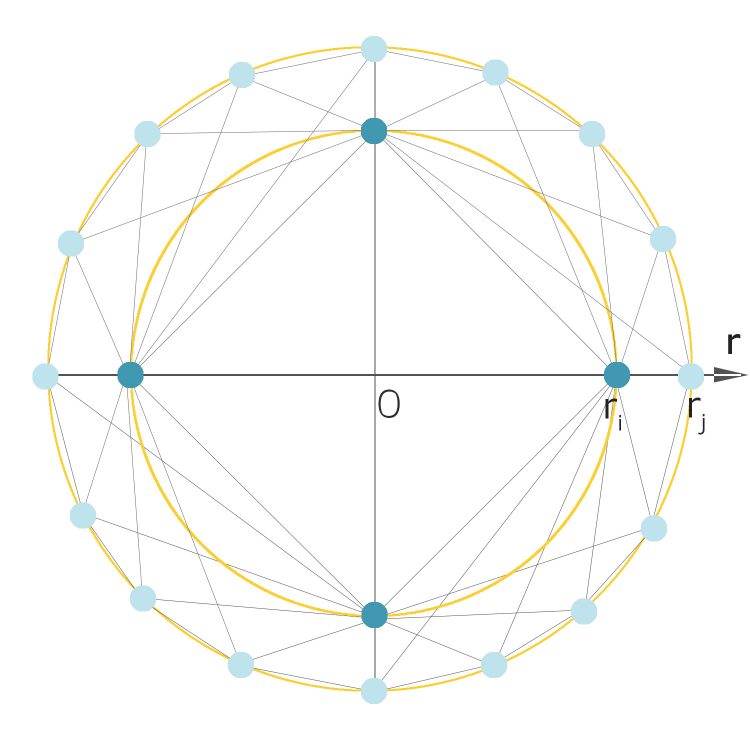
iv_34_Bild_8_08 — Topologie des Graphen.

Berechnung der Parameter für dieses Netzwerk

Rike Okay! Die Anzahl der Server ist

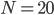
Zuerst berechne ich den mittleren Degree 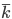. Die inneren Server haben jeweils 11 Edges, die äußeren 4, das ergibt:

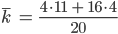
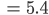
Wir nehmen wieder

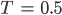
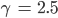
und kriegen

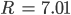
Die Radien der Vertices müssen wir nach der exponentiellen Dichteverteilung 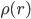berechnen. Warte mal, wir haben 4 innere Vertices, 4/20, das ist dann auch die Wahrscheinlichkeit dafür, dass ein Server auf diesem Radius ist. Mit der exponentiellen Formel vom letzten Mal kriegen wir

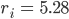
Und außen geht das genauso. Für

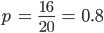
nehmen wir den äußeren Radius

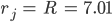
"Innere" Serververbindungen

Ben Ja schön, jetzt die Abstände! Lass uns die Abstände der inneren Server voneinander berechnen.

Rike Klar!

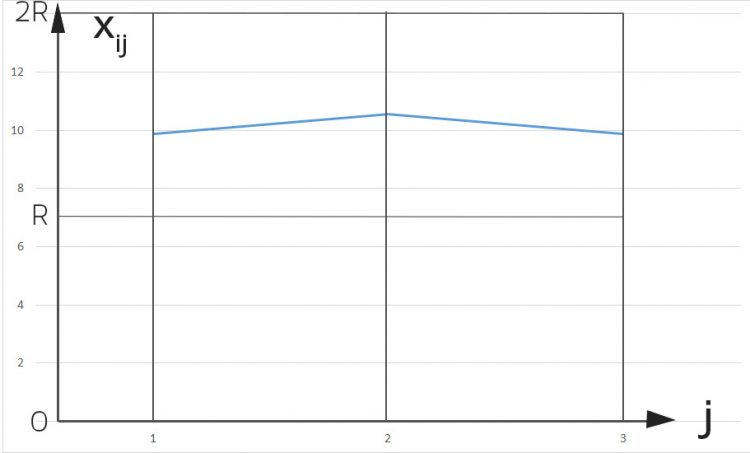
iv_33_hyperbol_abstand_server_server_x_03 — Hyperbolischer Abstand x_ij der inneren Vertices V_j zu einem anderen inneren.

Verbindungswahrscheinlichkeit

Ben Gut! Kannst Du auch noch zu jedem Abstand die Wahrscheinlichkeit p_ij berechnen. Das ist die Wahrscheinlichkeit für das Zustandekommen der Verbindung. Das Wichtigste! Die Formel geht so:

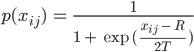
Rike Wo kommt die her?

Ben Das haben Boguná und seine Kollegen vorgeschlagen. Sie haben wohl einen quantenphysikalischen Background. Das ist nämlich die Fermi-Dirac-Verteilung.

Rike Okay, das lässt sich gut ausrechnen, warte…

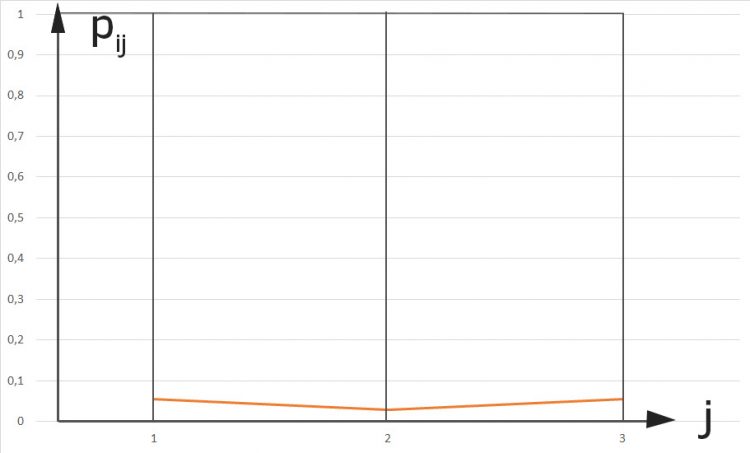
iv_33_hyperbol_abstand_server_serv — Verbindungswahrscheinlichkeit eines inneren Servers zu den anderen inneren

Serververbindung "Innen - Außen"

Ben Hmm, ziemlich klein. Na gut. Wie ist es mit den Entfernungen von einem inneren zu den äußeren Servern?

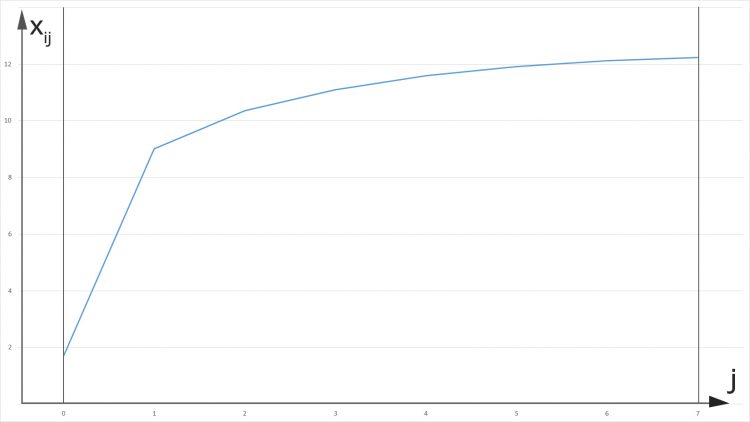
iv_34_hyperbol_abstand_PC_x_server_08 — Hyperbolische Abstände eines inneren Servers zu den äußeren Servern. In Bens Netzwerk ist ein Server allerdings nur mit einem Server (j = 0) direkt auf dem Durchmesser, 3 äußeren Servern (j=1,...4) nach rechts verbunden und mit 4 Servern nach links. Die Verbindungen sind symmetrisch nach rechts und links.

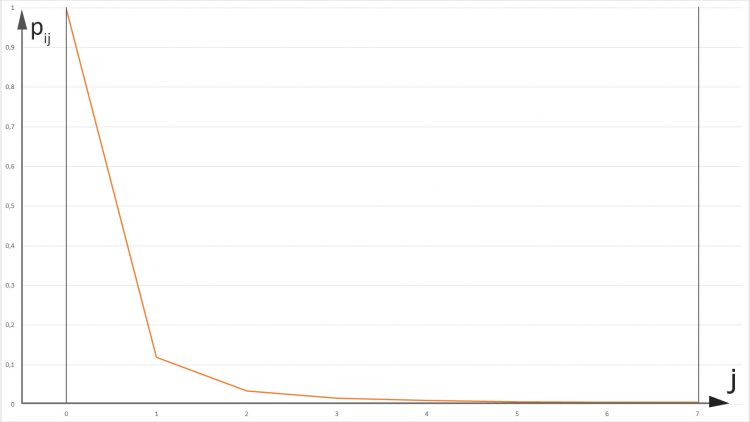
iv_34_hyperbol_abstand_PC_p_server_08 — Wahrscheinlichkeit p_ij dieser Verbindungen nach der Exponentialverteilung. Die Verbindung eines inneren Servers zu seinem direkten äußeren Nachbarn hat die Wahrscheinlichkeit 0.99.

Ben Schön! Das entspricht meiner Vorstellung von einem vernünftigen Computernetzwerk. Die nächsten Server werden mit der größten Wahrscheinlichkeit verbunden. Die größte Wahrscheinlichkeit hat der innere Server zu seinem nächsten äußeren. Die ist fast 1! Wow! Und was ist mit den äußeren Servern?

Verbindung eines "äußeren" Servers zu einem Nachbarn

Rike Die kann ich Dir auch ausrechnen, das ist wie bei letzten Mal. Die Verbindung zweier Nachbarn wird durch ihren Winkel bestimmt, den berechne ich zuerst:

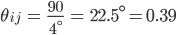
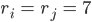
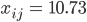
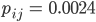
Visualisierung der hyperbolischen Abstände

Allerdings sind nur immer zwei äußere verbunden. Das Netzwerk ist symmetrisch. Die Entfernung ist ca. 11 Längeneinheiten. Das ist mehr als der Radius!

Ben Was, die Entfernung zweier äußerer Server ist länger als der Modellradius mit R = 7? Hmm. Unvorstellbar, diese Topologie.

Rike Lass uns überlegen. Wir haben einen gekrümmten Raum. Von oben sieht das Ganze ungefähr so aus:

iv_34_hyperbolisch_03_02 — Bens Netzwerk im gekrümmten Raum

Aber die Entfernungen am äußeren Rand werden immer größer, vielleicht so?

iv_34_hyperbolisch_06-08 — Bens Netzwerk mit Abständen (in türkis) und Verbindungswahrscheinlichkeiten (in orange)

Ben Okay! Super! Für mich ist das so neu, so unvorstellbar. Du bist vielleicht die erste, die so ein hyperbolisches Netzwerk zeichnet. Die anderen arbeiten nur die Formeln ab. Hm. Ich eigentlich auch, aber das weißt Du schon.

Rike Ist schon okay. Dieser gekrümmte Raum hat wohl noch viele Überraschungen für uns?

Ben Ja! Die exponentielle Wahrscheinlichkeit verstärkt den Effekt noch.

Rike Stimmt. Wofür stehen eigentlich die Parameter? Ein Netzwerk hat doch keine Temperatur!

Ben T kontrolliert wie die Temperatur die Clusterung, R steht für das chemische Potential.

Rike Na super!

Ben Rike, ich danke Dir. Jetzt kann ich richtig anfangen, die Parameter zu testen und so ein Netzwerk zu simulieren.

Rike Viel Spaß!

***

Übungsaufgabe

Berechne selbst ein kleines Einstein-Netz.