Lila und Jenny sind in Berlin unterwegs. Sie wollen am Potsdamer Platz in die U2 einsteigen und in Richtung Pankow fahren. Doch es ist sehr voll. Es ist so voll, dass sie auf die nächste Bahn warten. Aber die ist auch so voll. Lila fragt Jenny, ob das immer so ist.
Lila Sag mal, wie kommen wir da mit? Wird das auch mal besser?
Jenny Haha, in Stoßzeiten ist das ein Problem. Man kann das gut mathematisch modellieren, ich hab‘ da mal einen Bericht über das Fahrgastaufkommen gelesen und da habe ich mal ein Modell gemacht.
Lila Wie geht das?
Jenny Die U2 fährt von Ruhleben zum Alex und dann nach Pankow. Hier am Potsdamer Platz steigen sehr viele Leute um, Du siehst es ja. Man hat das gemittelt und herausgefunden, dass von Ruhleben bis zum Alex immer mehr Personen pro Minute im Mittel zusteigen.
Lila Was? Das ist ja fast wie in Kalkutta! Kennt man die Zahlen genauer?
Jenny Ja, in Ruhleben ist der Zug leer und erst nach und nach steigt jemand zu, warte, das muss ich nachschauen, der Anstieg wächst bis zum Alex auf 114 Personen pro Minute. Und danach nimmt die Belegung konstant ab, mit 166,667 Personen pro Minute, hier sieh:
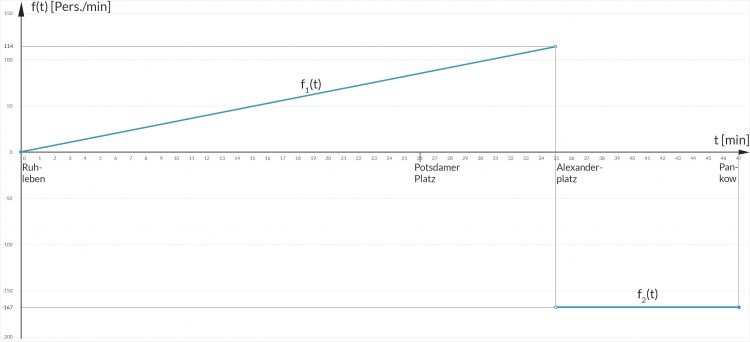
Lila Aha!
Jenny Ja, daraus kannst Du die Belegung zu jedem Zeitpunkt berechnen.
Lila Warum sagt ihr "Belegung"? Liegen die Fahrgäste?
Jenny Haha! Nein. Das ist ein richtiges Beamtenwort. Fahrgastbelegung, Fahrgastbesetzung, Fahrgastaufkommen...
Lila Deutsch ist sehr umständlich!
Jenny Ja, ich sehe das auch.
Lila Okay, und wie berechnest Du das?
Jenny Na, wir kennen die Änderung der Fahrgastanzahl f(t) in jedem Augenblick, dann können wir das integrieren.
Lila Waaas?
Differentialgleichung mit Anfangswertproblem für die Fahrgastbelegung der U2
Jenny Lass uns die Fahrgastanzahl mit x(t) bezeichnen und die Änderung der Fahrgastanzahl mit f(t), dann wird die Änderung der Fahrgastanzahl durch unser f(t) beschrieben, eine einfache Differentialgleichung...
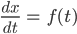
und der dazu gehörige Anfangswert ist
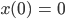
Das ist eine lineare, gewöhnliche Differentialgleichung, die kann man direkt integrieren.
Stückweise rechte Seite f(t)
Warte, wir haben für das 1. Intervall 0 < t < 35 min:
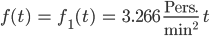
und im 2. Intervall 35 min < t < 47 min – vom Alexanderplatz bis nach Pankow:
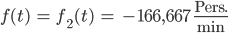
Stückweise Integration
Das integriere ich! Im 1. Intervall kriege ich
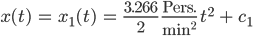
Und im 2. Intervall:
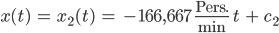
Lila Und was ist mit der Konstanten?
Bestimmung der Konstanten
Jenny Na, in Ruhleben soll der Zug leer sein, das ist der Anfangswert:
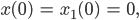
Also ist
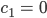
Und beim Alexanderplatz gehe ich davon aus, dass da die Lösung stetig ist, dass also die Werte für die beiden Funktionen gleich sind:
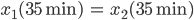
Lila Okay, das kann ich auch!
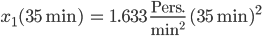
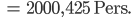
Haha – und andererseits
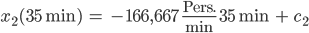
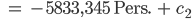
Richtig?
Jenny Richtig!
Lila Dann setze ich die beiden Seiten gleich und kriege für 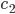 :
:
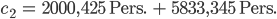
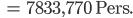
Wow! Dann haben wir’s gelöst:
Stückweise Lösung
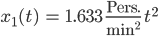
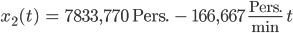
Jenny Super, Lila, das kommt eigentlich erst viel später im Studium dran!
Lila Danke! Dann können wir ausrechnen, wie viele Leute jetzt in der U-Bahn sind?
Jenny Ja, klar, von Ruhleben bis hierher sind 26 Minuten eingeplant.
Lila Okay! Das ergibt 1104 Leute! Und am Alex sind es 2000 Leute? Wahnsinn!
Jenny Das ist der ganz normale Wahnsinn in Berlin!
***
Übungsaufgaben
- Überprüfe die Besetzung am Ende, nach 47 Minuten.
- Ist die Lösung diffbar?
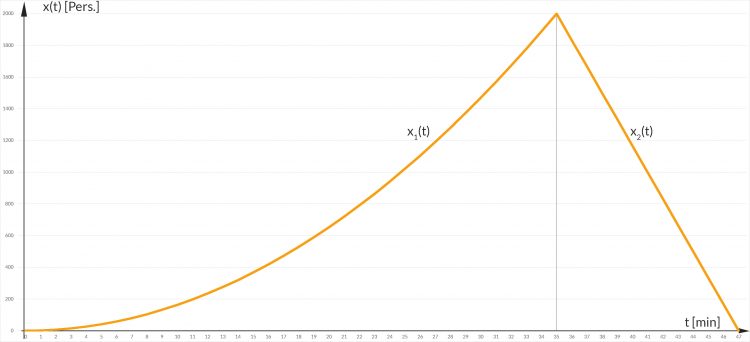
- Zeichne die Lösung!
Lösungen
- x(47 min) = 0
- Nein, in t = 35 min ist sie nur stetig.