Lila hat nun ihr Studium begonnen. Sie hat sich für ein technisch orientiertes Mathestudium an einer Berliner Uni entschieden. Am liebsten mag sie die Informatik-Vorlesungen. Jetzt hat sie etwas über Warteschlangen gehört. Das ist eine Methode, wo man in eine Liste immer nur Dinge an der einen Seite hinzufügt und auf der anderen Seite wegnimmt. First-In, First-Out. Wie bei der U-Bahn denkt sie. Es kommen Leute rein und gehen welche raus. Sie überlegt, ob sie damit Jennys kontinuierliches Modell nicht viel besser machen kann.
Sie wählt wieder die TigerJython-Umgebung für Python. Sie hat es fast liebgewonnen – nach anfänglichen Umständlichkeiten. Darin sind diese Befehle bereits vorgesehen:
liste.append(n)
liste.remove(m)
Der 1. Befehl hängt an die Liste liste den Wert n an die letzte Stelle an, der 2. Befehl entfernt den Wert m, der zuerst in der Liste steht. Außerdem kann man sehr gut auf die ersten und letzten Elemente der Liste zugreifen:
liste.first
liste.last
Doch wie soll sie vorgehen? Es gibt so viel zu bedenken. Sie macht zuerst ein kleines Schema, wie das mit einer kleinen U-Bahn und wenigen Passagieren ablaufen soll:
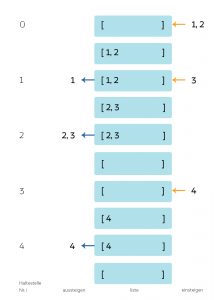
Funktionalitäten der Warteschlange
- An der Anfangsstation sollen 2 Passiere einsteigen, Keiner steigt aus. Dieses Keiner steigt aus soll dann auch für jeden Durchlauf gelten.
- An der 1. Station soll 1 Person aussteigen und 1 einsteigen.
- An der 2. Station sollen 2 Personen aussteigen und keine einsteigen. Der Zug fährt leer weiter. Das kommt zwar in Berlin nicht oft vor, aber sie muss das testen.
- Keiner steigt aus, einer steigt ein. Das ist die 4. Person. Die mitfahrenden Personen will sie mitzählen.
- An der Endstation soll der eine Passagier aussteigen, keiner steigt ein. Auch das soll allgemein gelten, keiner soll einsteigen.
Implementierung
Na, gut denkt sie, dann mache ich eine Liste passengers, da werden die mitfahrenden Passagiere hineingetan, genau wie in der Skizze. Die Aussteigenden sollen von vorn gelöscht werden, die Einsteigenden sollen hinten hinzukommen. Das geht dann so
passengers.remove(passengers.first)
passengers.append(pass_max)
pass_max ist die aktuelle Nummer des letzten Passagiers. Steigen mehrere ein oder aus, muss das mehrfach gemacht werden, sie braucht dazu eine Schleife, für die sie
repeat n_out
bzw.
repeat n_in
benutzt, wobei n_out und n_in die aktuelle Anzahl der aus- und einsteigenden Passagiere ist. Nur bei der 0. Haltestelle soll keiner einsteigen, den Fall ( i = 0 ) muss sie prüfen und das Aussteigen verweigern bzw. bei der letzten Haltestelle ( i = BOUND - 1 ) soll keiner einsteigen, das muss sie prüfen und das Einsteigen verweigern.
Sie muss die Länge der Liste prüfen, wenn die Liste leer ist, muss die letzte Nummer des letzten Passagiers kennen und die um 1 erhöhen:
if len(passengers) != 0:
passengers.append(passengers.last+1)
Sie muss die Haltestellen mitzählen und eine Variable dafür bereithalten, das soll dann i sein. Am besten, sie hält die maximale Anzahl der Haltestellen variabel. Die U2 hat 29 Haltestellen, das ist etwas lang zum Testen. Also haben wir noch eine Variable BOUND für die Anzahl der Haltestellen.
Ermittlung der Umsteigezahlen
An jeder Haltestelle fragt sie nach der Anzahl der aus- und einsteigenden Passagiere n_out und n_in und merkt sich diese für einen Augenblick, um die mittlere Anzahl der Umsteiger zu ermitteln und die Liste passengers zu editieren:. Die Anzahl der Umsteiger ist
transfer
und berechnet sich aus
transfer = n_in - n_out
Wenn man alle diese transfer-Werte an jeder Haltestelle aufsummiert und durch die Anzahl der Haltestellen teilt, kriegt man die mittlere Anzahl der Umsteiger.
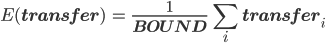
Usability
Als sie das testet, klappt noch nicht alles so. Sie möchte manchmal das Programm abbrechen, weil es zu lang zum Testen ist oder bereits ein Fehler aufgetaucht ist. Außerdem muss sie mit Abbrüchen der User rechnen, auch das hat sie schon in der Vorlesung gelernt. Was kann von Userseite passieren?
- Der User gibt keine ganze Zahl für die Anzahl der Haltestellen ein.
- Der User bricht an dieser ersten Abfrage das Programm ab.
- Der User bricht die Angabe der ein- oder aussteigen Passagiere ab.
- Der User lässt mehr Leute aussteigen als im Zug sind.
- Der User lässt Passiere aus dem „leeren“ Zug aussteigen.
- Der User gibt negative Anzahlen ein.
Dennoch soll in solchen Fällen das Programm zu Ende ausgeführt werden und ein Ergebnis angezeigt werden. Schließlich schafft sie es doch (bis auf die negativen Eingaben). Sie hat richtig Spaß daran, sie könnte auch für Alles eine Datenbank schreiben und die Zeit beim Mitfahren dazu notieren. Aber für heute ist es erst einmal genug, denkt Lila.
Lilas Code
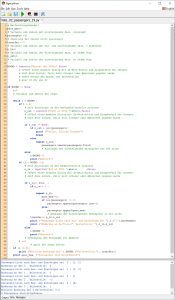
Als sie das nächste Mal Jenny am Potsdamer Platz trifft, zeigt sie ihr das Warteschlangen-Programm.
Lila Jenny schau‘ mal, ich habe die U2-Situation mit einer Warteschlange FIFO modelliert.
Jenny Eine FIFO-Warteschlange?
Lila Ja, First-In, First-Out! Die Passagiere, die zuerst gekommen sind, dürfen zuerst aussteigen und die neuen müssen immer hinten dran.
Jenny Haha! Da möchte ich nicht mitfahren! Aber zeig mal!
Lila Hier teste doch mal!
***
Übungsaufgaben
Schreibe selbst ein Warteschlangenprogramm und mache ein Flowchart dazu!
