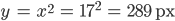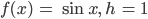Max und Charly machen Osterferien. Max sucht immer noch einen Job, Charly hat eine Stelle an einer Schule als Lehrer für Mathe und Sport gefunden. Er ist Quereinsteiger. Sie sind zum Hohen Stein ins Sauerland gefahren. Eigentlich sind sie eher die Läufer und Ballspieler, aber heute wollen sie mal einen Felsen erklimmen.
Charly erzählt von seiner ersten Zeit als Lehrer. So soll er in der Sekundarstufe 1 auch Informatik unterrichten. Da gibt es eine Programmentwicklungsumgebung für Kinder: TigerJython, das soll er nehmen. Es ist eine “Kinderversion” von Python. Als didaktisches Konzept wird die Schildkröte Turtle eingeführt, die wie ein Stift funktioniert. Man lässt sie durch die Befehle FORWARD(), LEFT() und RIGHT() "zeichnen". Mit diesen Befehlen geht die Schildkröte eine bestimmte Länge vorwärts und mit den anderen Befehlen dreht sich die Schildkröte um einen bestimmtem Winkel nach links bzw. rechts. Diese Grafik-Tools dienen wegen der besonderen Anschaulichkeit als Einstieg ins Programmieren.
Charlys Problem
Nachdem Charly mit Turtle genug forward, left und right gegangen war, versuchte er nun, damit mathematische Funktionen wie
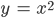
zu zeichnen und – verzweifelte. Nun fragt er Max.
Max Wie startet denn die Schildkröte?
Charly Sie steht in Bildmitte und blickt nach oben, nach Norden. Achsen mit Bezeichnung und Skalierung gibt es nicht. Die denken wir uns! Wenn ich
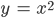
mit Start im Nullpunkt zeichnen will, muss ich sie erst einmal um 90° nach rechts drehen. Das ist klar.
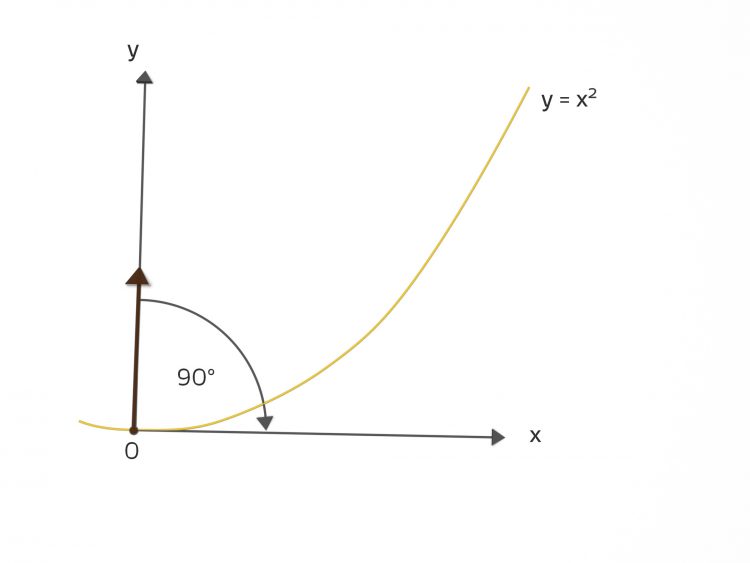
Der erste Schritt der Turtle für die Kurve y = x²
Max Ja gut.
Charly Dann habe ich weiterüberlegt, in welche Richtung sie nach einem kleinen Schritt geht. Sie schaut also nach rechts, aber die Parabel steigt an.
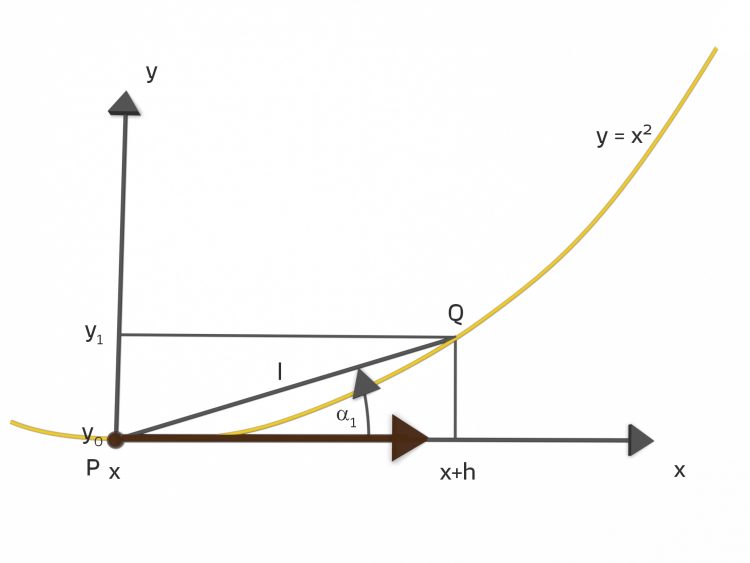
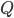gehen, 
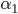ist der Anstiegswinkel der Strecke 
, 
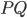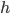soll die Schrittweite in 
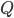-Richtung sein.Ich würde zum Punkt gehen, nicht geradeaus. Das ist doch eine gute Näherung. Am Felsen klettern wir doch auch schräg nach oben!
Max Gut, eine Treppennäherung wäre wirklich die allerletzte Idee.
Charly Dann muss sich die Turtle um 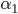drehen; und ich muss den Winkel 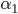berechnen. Das geht so:
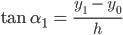
Aber weißt Du, das erinnert mich an die 1. Ableitung. Der Tangens von 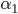ist ein Differenzenquotient und n ä h e r t die 1. Ableitung einer Funktion an. Ich fand das zu krass!
Max Hmm, echt krass! Aber lass uns einfach geometrisch weitermachen, so einen Anstieg können wir uns doch ganz gut vorstellen, oder? Nach dem Winkel 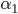umgestellt ergibt das:
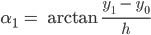
Die Turtle geht um 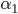nach links.
Charly Den Winkel muss man noch ins Gradmaß für die Turtle-Grafik umrechnen. Na gut, und die Schrittlänge ist 
, nehmen wir den guten alten Pythagoras:
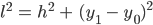
Mensch, Max, ist gar nicht schwer,
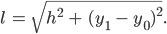
Aber dann stehen wir in 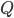, schauen in die Richtung von eben und müssen ein neues Koordinatensystem einführen. Das fand ich auch etwas zu heftig. Was meinst Du?
Die nächsten Turtle-Schritte
Max Lass uns das zeichnen:
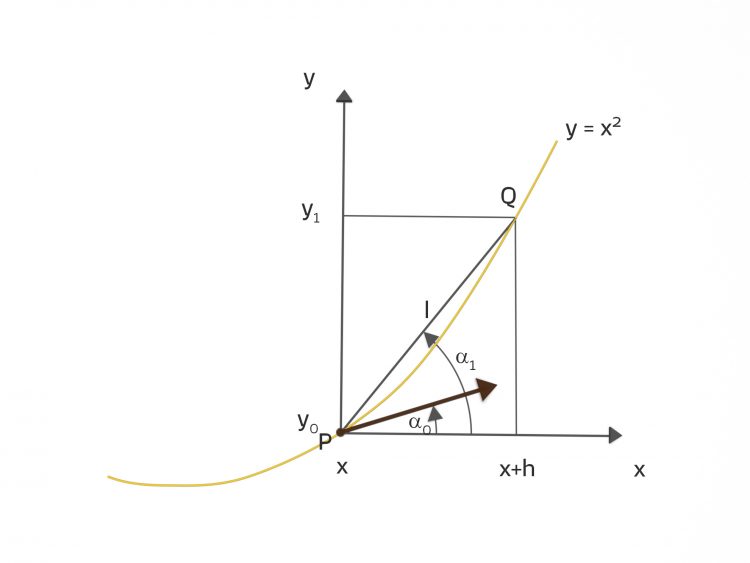
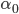wird nun der letzte Anstiegswinkel bezeichnet, mit 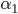der für den nächsten Schritt.Du nimmst ein neues Koordinatensystem. Es wandert mit der Schildkröte mit, das ist fast wie mit der Relativitätstheorie, haha! Du nimmst jetzt Deinen „alten“ Punkt 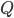für den neuen Startpunkt 
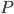, den alten Winkel 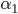musst Du Dir merken, den bezeichnest Du jetzt mal mit 
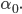Und nun versuchst Du wieder, ein Stück weiterzugehen. Du rechnest wieder die Neigung Deines Schrittes zu 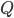aus, das ist 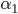nach der Formel wie oben, Du rechnest die Länge Deines Forward-Schrittes aus, und drehst Dich um die Differenz
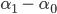
nach links!
TigerJython-Code
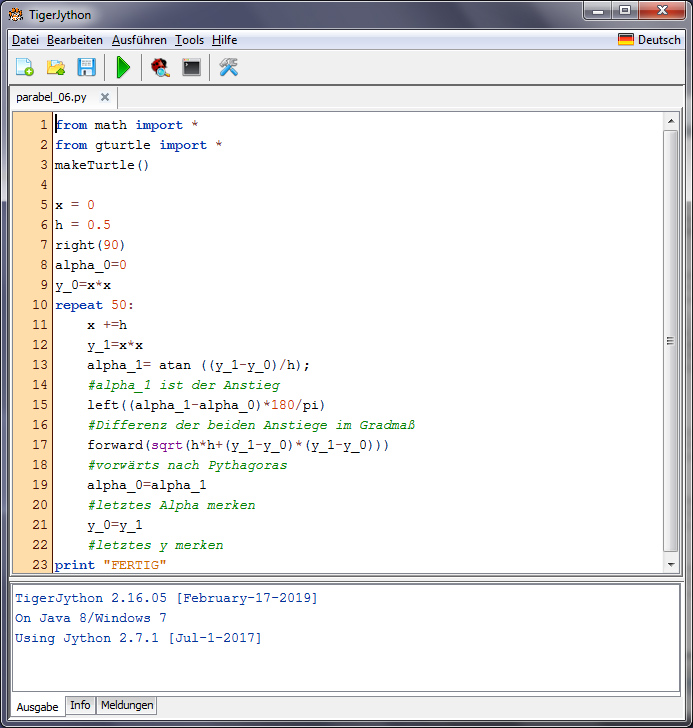
Charly Okay, verstehe. Das kann ich dann gut wiederholen und in eine Schleife packen! Wir versuchen‘s! Ich muss es eben programmieren:
Max Hey! Lass mal laufen!
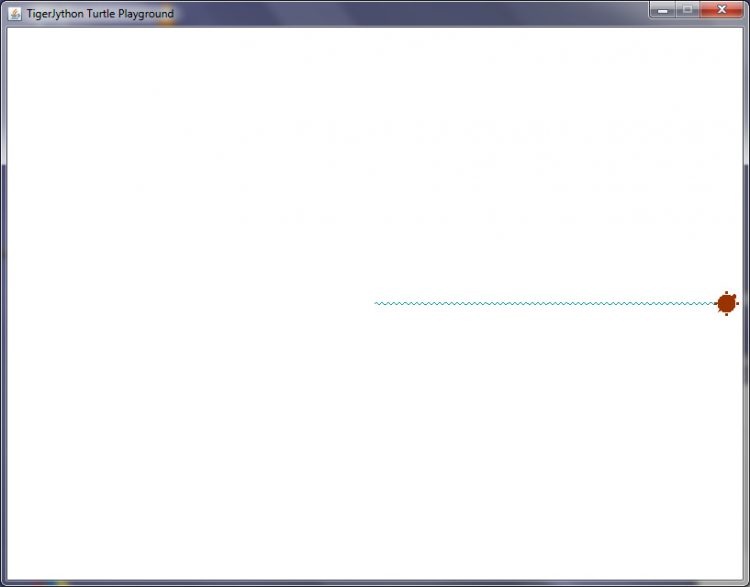
Ausführung in der TigerJython-Umgebung
Charly Hier:
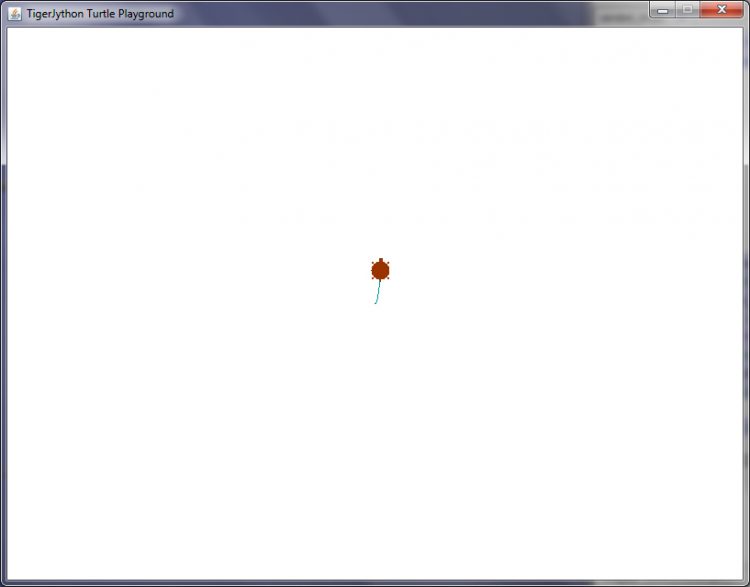
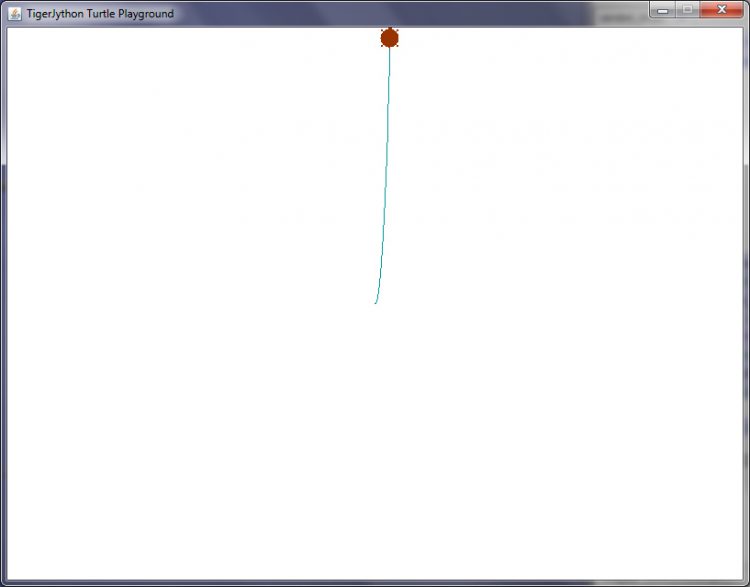
Max Okay! Nicht sehr schön, aber witzig, wieso läuft sie denn aus dem Fenster hinaus?
Charly Ist ein statisches Fenster, 800 x 600 px.
Max Ach so! Ist die Kurve nicht ein bisschen steil für eine Normalparabel? Welche Schrittweite hast Du denn?
Charly Die Schrittweite ist 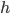, die habe ich variabel gelassen, wie man das so macht, jetzt hab' ich mal
gesetzt, eigentlich soll die Schrittweite ja sehr klein sein, eher so im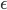 
-Bereich, hab' ich gelesen, aber das klappt hier nicht.
Max Es sieht so aus, als wäre eine Längeneinheit ein Pixel. Na! Für welche Klasse ist das denn?
Charly Für die 7.!
Max Kleine Herausforderung, das einer 7. Klasse zu erklären. Dann musst die Differenzialrechnung geometrisch erklären, Du hast veränderliche Koordinatensysteme, Du brauchst die Arkustangens- und die Wurzel-Funktion, und das alles, um eine Parabel zu zeichnen!
Charly Ach, vielleicht sollten wir die Stunde hier am Hohen Stein machen, das ist wirklich anschaulich.
Max Hahaha!
***
Übungsaufgaben
- Stimmt es, dass die Längeneinheit 1 Pixel ist – bei Fenstergröße von 800 x 600 px?
- Was passiert, wenn man die Schrittweite h = 1 setzt?
- Programmiere die grafische Darstellung einer Funktion Deiner Wahl mit FORWARD(), RIGHT() und LEFT()!
Lösung
- Ja, nach 34 Schritten à 0.5 px haben wir eine Länge von 17 px in -Richtung und
nach oben. Da ist sie fast die halbe Fensterhöhe durchlaufen.
- Da ist sie nach 19 Schritten schon aus dem Fenster herausgelaufen.
, 384 Schritte
