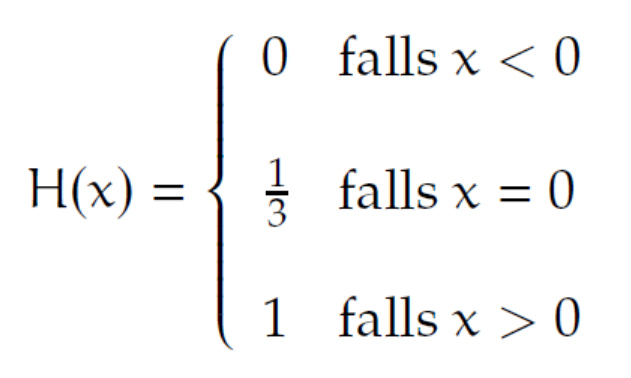Ben soll morgen Allen genauer den Unterschied flacher und tiefer neuronaler Netze erklären. Er versucht wieder, Rikes Katze Molly zu fotografieren und aus verschiedenen Katzenfotos Molly digital zu rekonstruieren. Doch die Katze ist manchmal unscharf fotografiert, Ben ist ja nur Informatiker. Wie kann man das dann aus unscharfen Fotos entscheiden?
Ben Stell Dir vor, ich habe 1-Megapixel-Bilder und soll von jedem Bild entscheiden, ob das Molly ist oder nicht, dann habe ich eine "tolle" Aufgabe! Jeder Pixel hat 256 Grauwerte, nehmen wir mal nur ein Schwarz-Weiß-Bild!, dann sind prinzipiell
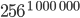
verschiedene Bilder als Eingang in mein Programm möglich!
Aufgabenstellungen für neuronale Netze
Rike Wow!
Ben Das sind mehr als das Universum Atome hat!
Rike Also gibt es keinen Rechner in diesem Universum, der das entscheiden kann?
Ben Doch! Wir müssen das intelligenter machen, wir lassen verschiedene Abstraktionsniveaus zu, das nennt man Deep Learning. Es sind einige Arbeiten herausgekommen, die untersuchen, was tiefe neuronale Netze leisten können. Die Grundideen kann ich Dir erklären.
Rike Dann mal los!
Ben Lass uns das erstmal prinzipiell diskutieren, bevor wir zur Bilderkennung kommen. Bisschen mathematisch, das gefällt Dir bestimmt!
Rike Klar!
Ben Die Eingangsdaten sollen die Vektoren
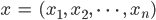
sein und
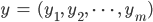
die Modellparameter, die Katzenparameter. Mit normalen, klassischen Straight Forward-Methoden kann man die Wahrscheinlichkeit des Eintretens der Ereignisse 
und 
berechnen.
Klassifikation
Eine typische Aufgabe ist die der Klassifikation, das ist die Wahrscheinlichkeit des Auftretens des konkreten -Katzenmodells für gegebene Eingangsdaten , das schreibt man
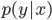
Rike Klar.
Vorhersage
Ben Die Vorhersage der Daten für ein Modell schreibt man
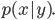
Das ist die Wahrscheinlichkeit des Bildes – also der -Werte für eine -Katze, also für Molly. Katzen bleiben ja nie still sitzen und werden unter verschiedenen Bedingungen, Perspektiven und mit verschiedenen Kameras fotografiert.
Rike Und Fotografen lernen noch.
Ben Hm, jedenfalls ist es gar nicht so leicht, in einem Molly-Bild, Molly zu entdecken.
Rike Mann, es hört sich kompliziert an, mathematisch sind das aber nur bedingte Wahrscheinlichkeiten.
Satz von Bayes
Ben Stimmt. Mit dem Satz von Bayes kann man dann das eine aus dem anderen berechnen:
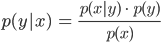
Und wenn Du mehrere verschiedene Katzenmodelle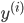 
hast, dann geht der bayessche Satz so
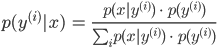
Rike Alles klar!
Ben Das ist die Mathematik der flachen neuronalen Netze.
Rike Gut, und die tiefen?
Mathematische Beschreibung neuronaler Netze
Ben Du weißt ja schon, dass es verschiedene Levels gibt.
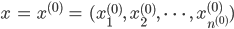
sollen die Eingangsdaten sein,
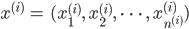
sollen die Daten des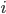 
-ten Levels sein. Vom 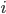-ten Level kommt man zum 
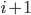-ten Level durch
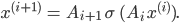
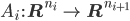
sind Transformationen
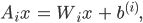
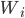sind Matrizen, 
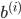sind Vektoren und
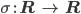
wird komponentenweise angewendet. Diese Transformationen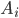 
beschreiben das Sortieren von Daten, das Multiplizieren mit konstanten Faktoren und die Addition von Konstanten. Das lässt sich gut implementieren. Der wirkliche Knackpunkt ist die Funktion 
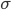. Sie steht für Entscheidungen oder Berechnung von Wahrscheinlichkeiten.
Rike Verstehe.
Ben Nun stellt sich die Frage, welche mathematischen Funktionen 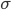überhaupt durch neuronale Netze dargestellt oder angenähert werden können.
Rike Na, ich würde mit Polynomen anfangen. Mit Polynomen kannst Du jede stetige Funktion auf einem endlichen Intervall gleichmäßig annähern, das garantiert der Approximationssatz von Weierstraß. Lineare Abbildungen hast Du ja schon.
Ben Stimmt. Die erste nichtlineare, nichttriviale Funktion mehrerer Veränderlicher wäre das Produkt von Zahlen. Da habe ich die Arbeit von Lin, Tegmark und Rolnick gefunden, die untersuchen genau das.
Rike Erzähl' mal!
Eine Methode für das Produkt mehrerer boolschen Werte
Ben Stell' Dir vor, Du sollst ein Programm schreiben, um 
Zahlen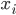 
miteinander zu multiplizieren. Als einfachsten Einstieg haben die Drei nur Zahlen 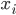genommen, die nur boolesche Werte annehmen, also nur 1 oder 0.
Rike Na, gut, das macht es einfacher. Du fragst alle Werte ab, und wenn alle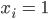 
, dann ist das Produkt auch 1.
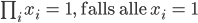
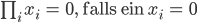
Ben Rike, das ist richtig, doch es ist nur ein flaches neuronales Netz. Da musst Du für große zu viele Fälle abfragen.
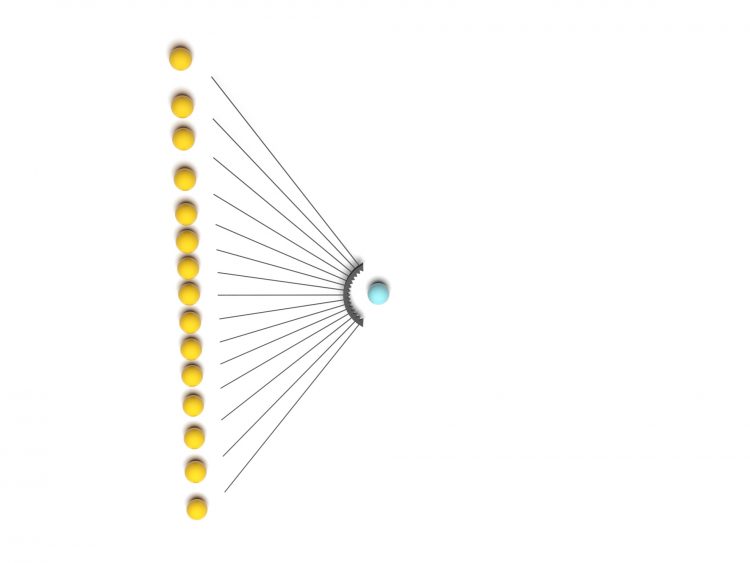
Rike Stimmt. Was haben sich die Herren ausgedacht?
Ben Das Produkt ist genau dann 1, wenn alle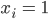 
sind, und das ist der Fall, wenn die Summe ist:
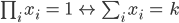
Dieser Test, ob die Summe von Zahlen ist, macht man mit der Sigmoidfunktion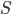 
:
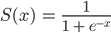
Rike Warte mal. Okay. Sieht so aus:
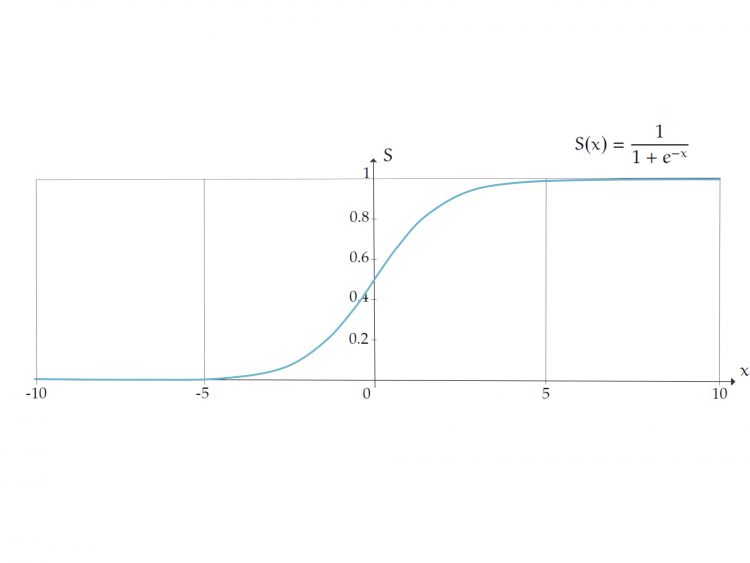
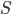
Ben Richtig. Diese Sigmoidfunktion muss ich für einige -Werte implementieren, aber es reicht schon von -10 bis 10. Wenn ich nun Zahlen 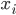habe und das Produkt bestimmen will, dann berechne ich zuerst
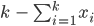
Die Frage, ob das entweder 0 oder 1, 2, 3, ... ist, prüfe ich, indem ich 1/2 abziehe, dann kriege ich entweder -1/2 oder 1/2, 3/2, 5/2, ... Mit einem Faktor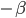 
, 
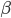soll sehr groß sein, na, 10 reicht schon, kann ich die Differenz zwischen den beiden Fällen noch verstärken. Darauf wende ich dann die Sigmoidfunktion an:
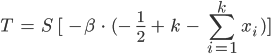
Rike Warte, ist die Summe gleich , wird 
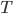zu
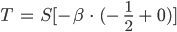
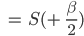
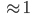
Ben Stimmt.
Rike Und falls nicht alle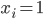 
sind, kriegen wir
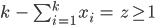
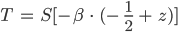
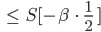
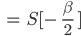
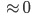
Produktformel
Ben Super, Rike! Du hast gerade deren Produktformel hergeleitet:
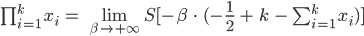
Rike Hey!
Ben Wir haben nun ein neuronales Netz, indem wir erst die Zahlen addieren, dann die Sigmoidfunktion anwenden und Beta groß werden lassen. Das sind zwei Levels und geht recht schnell.
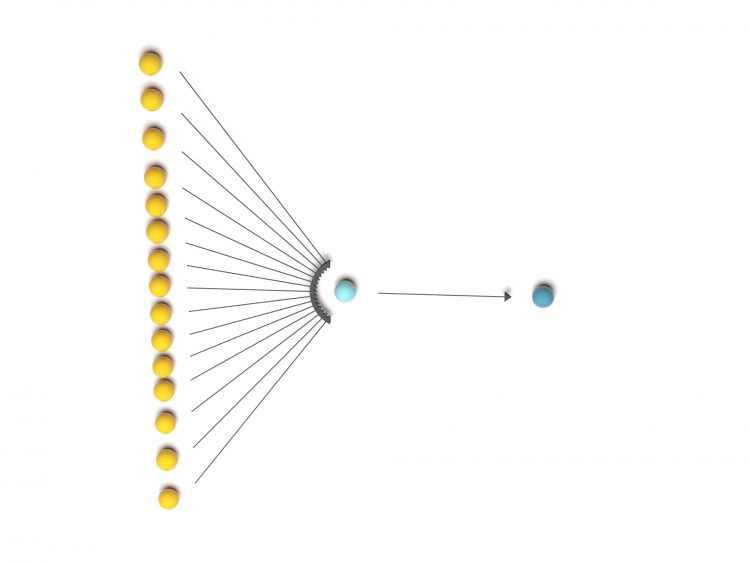
Rike Hey, mir gefallen neuronale Netze und so eine coole Produktformel!
***
Übungsaufgabe
Ist die Methode an die konkrete Sigmoidfunktion gebunden? Wenn nein, mache einen anderen Vorschlag und korrigiere die Produktformel!
Lösungen
1. Eine verifizierte Heaviside-Funktion H(x)
erfüllt die Bedingungen:
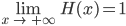
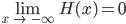
Die Produktformel bleibt unverändert:
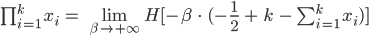
2. Auch die verifizierte Arcustangensfunktion
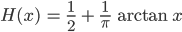
hat diesen Eigenschaften. Die Produktformel bleibt unverändert.