Charly besucht Max am Wochenende in Lemgo. Sie sind Mountainbike gefahren, Charly hat bei Max' Handball zugeschaut und nun wollen sie am Abend ein Bier trinken. Als er Max den Handball zuwerfen will, fliegt der Handball in einem merkwürdigen Zickzack.
Max Hey, was war das?
Charly Hey, Dein Ball ist verhext! Der fliegt nicht normal.
Max Der ist nicht verhext! Bei Dir stimmt was nicht, kannst Du den nicht in einem kleinen Bogen mir zuwerfen, ganz leicht? Wir lernen das im Training in allen Lebenslagen, auf dem Bauch, beim Sprung, rückwärts laufend, durch die Beine usw.
Charly Ich glaub, ich habe zu viel über meine Python-Programme und Vielecke nachgedacht, ich werde einfach nicht glücklich damit.
Funktionen in TigerJython
Max Was ist los?
Charly Mein Lehrbuch bietet ein Programm an, mit dem Girls and Boys auf “didaktisch wunderbare” Weise Funktionen kennenlernen. Dort heißt das zwar nicht Funktion, sondern Befehl, und eine Funktion, die in dem Buch Befehl genannt wird, besteht natürlich aus mehreren Befehlen …
Max Hahaha, hört sich wie eine rekursive Funktion an und wie beim Zauberlehrling!
Charly Okay, haha, damit komme ich schon klar. Ich hasse es, die Dinge zu verniedlichen und dann am Elternabend den Eltern-IT-Spezialisten die „Didaktik“ dahinter zu erklären. Kannst Du Dir vorstellen, so eine junge Mutter, die mit 3 Notebooks unterm Arm ankommt, von Befehlen in Befehlen zu überzeugen?
Max Wie sieht sie denn aus?
Charly Verdammt gut!
Max Hey!
Charly Na, okay, das ist nicht wirklich das Problem …
Max Was ist denn Dein Problem?
Die Vieleck-Funktion für die Turtle-Grafik
Charly Ich soll eine Funktion mit Parametern erklären, die ein 
-Eck zeichnet. Das und die Seitenlänge sollen variabel bleiben.
Max Ist das zu schwer? Mal doch mal ein Bild!
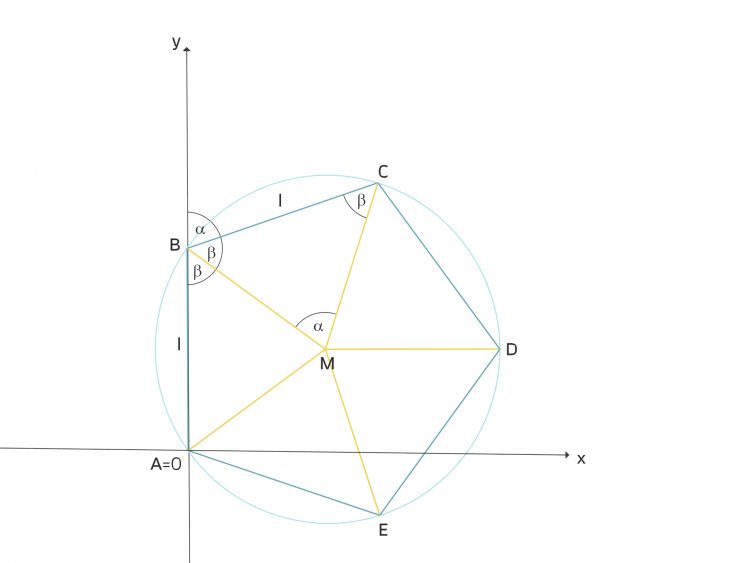
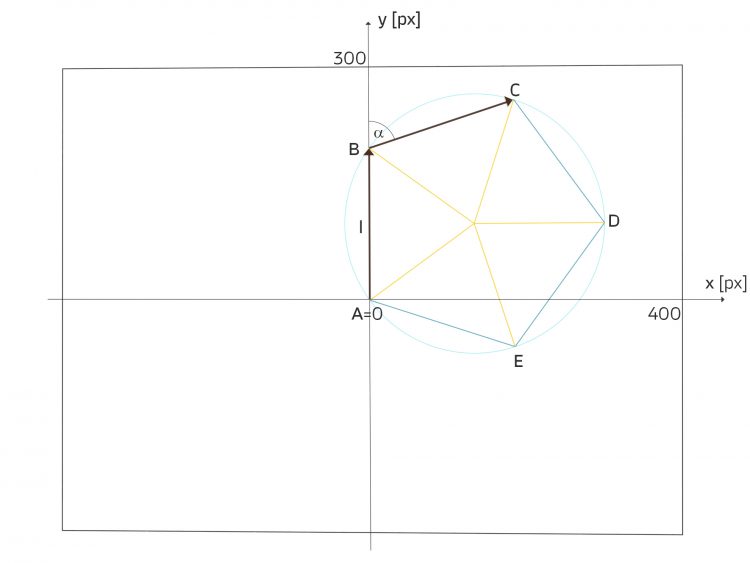
Charly Das vorgegebene Verfahren beruht auf der Idee:
Du sollst ein -Eck im vorgegebenen Fenster zeichnen, im Nullpunkt starten und dann 
Pixel nach oben gehen. Dann sollst Du Dich um den Winkel 
nach rechts drehen und wieder Pixel geradeaus gehen.
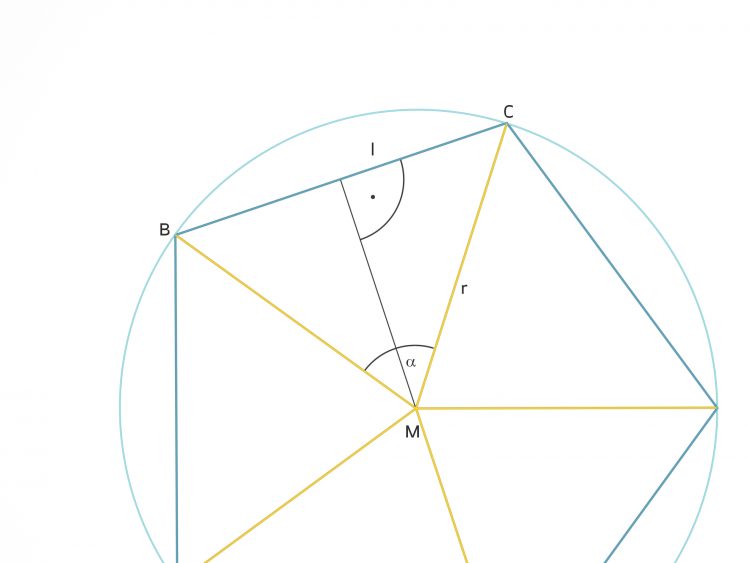
Max Hm. Wie groß ist ?
Charly Das siehst Du an der Zeichnung. Zunächst ist am Mittelpunkt des Kreises
Max Okay.
Charly Dann siehst Du im Dreieck MBC:
Und am Punkt B siehst Du dann, dass
ist, dass die Turtle sich wirklich um denselben Winkel nach rechts drehen muss.
Max Und weiter?
Charly Die Funktion vieleck mit den beiden Parametern anzahl_ecken – das ist unser – und der Seitenlänge seitenlaenge soll dann dafür sorgen, dass die Turtle Schritte geradeaus geht, sich um nach rechts dreht, und das -mal. ist die Seitenlänge unseres -Ecks, also die Länge der Strecke AB.
360-Millionen-Eck
Max Verstehe. Läuft die Turtle dann wieder zum Fenster hinaus?
Charly Ja, richtig, wenn zu groß ist, läuft sie zum Fenster hinaus, man müsste das abschätzen, aber auch für kleine und große läuft sie zum Fenster hinaus, hier schau mal:
Für
kriege ich so ein „360-Millionen-Eck“:
Da musste ich die halbe Nacht drauf warten, die Rechnung hat mein Notebook blockiert, ich konnte überhaupts nichts machen, hab nur gewartet!
Max Oh, Mann! Da kannst Du im Unterricht Probleme kriegen, wenn Deine Girls and Boys große Zahlen eingeben und unbedingt das Ergebnis abwarten wollen? Musst Du dann die Eltern anrufen und einen Shuttle organisieren?
Charly Haha.
Max Aber sag mal, ist das Ergebnis richtig? Sollte da nicht sowas wie ein Kreis rauskommen?
Charly Hm! Was weiß ich! Aber noch schlimmer ist, wenn einer dieser coolen Kids für verrücktes Zeug eingibt!
Das Problem fehlender Datentypen
Max Wieso denn das?
Charly Die Herleitung klappt natürlich nur für natürliche 
. Das kleinste sinnvolle Beispiel ist das Dreieck.
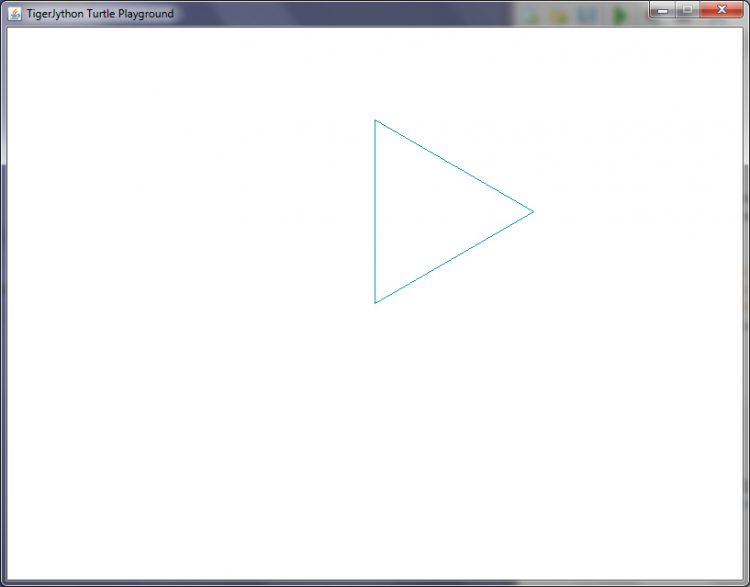
Aber in TigerJython gibt es keine Datentypen! Du kannst nicht einfach als Integer deklarieren und als Eingabe nur Integer akzeptieren. So – wie das in anderen Programmiersprachen üblich und nützlich ist! Diese fehlenden Datentypen werden sogar als großer Vorteil gefeiert. Du kannst anstelle von alles Mögliche eingeben: eine negative Zahl, eine Zeichenkette, Null oder auch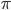 
:
Dann kriegst Du für den Winkel :
Das wird -Mal wiederholt. In Python, was als Programmiersprache dahintersteckt, wird eine Schleife nicht 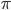-mal ausgeführt, sondern für die Anzahl der Durchläufe wird intern in eine ganze Zahl generiert, in dem Fall kommt 3 raus. Das habe ich morgens um 4 nach dem missglückten 360-Millionen-Eck noch herausgefunden.
Max Oh, Charly, wie hälst Du das durch?
Charly Hm, mit Humor!
Max Super. Also, für ein Pi-Eck dreht sich die Turtle 3-mal um 114.59°, richtig? Das sind
Dann kommt sie nicht wieder am Nullpunkt an!
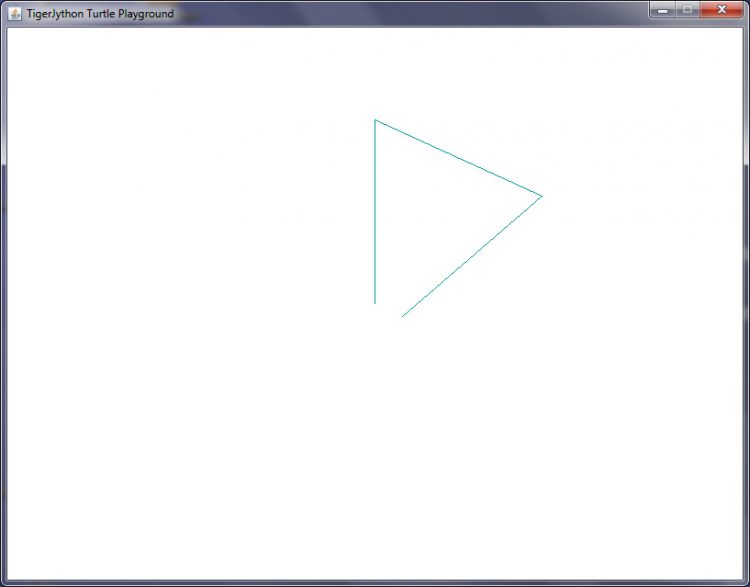
Ach, Charly, so ein Pi-Eck ist doch wirklich sooo cool. So was macht bestimmt beim nächsten Elternabend großen Eindruck!
Charly Hahaha!
***
Übungsaufgaben
- Was passiert mit diesem Algorithmus für
? - Schreibe das Programm dafür!
- Wie sieht damit ein 2-Eck aus?
- Wie sieht damit ein e-Eck aus?
Lösungen
- Dann wird der Winkel
Den Radius
des Kreises kann man berechnen.
Es ist
Und folglich
Für
ergibt das einen Radius
von
Dieses 360-Millionen-Eck mit einem Umkreisradius von 106 px passt nicht in das 800 x 600 px-Fenster. Es zeigt nur die ersten und letzten Teile.
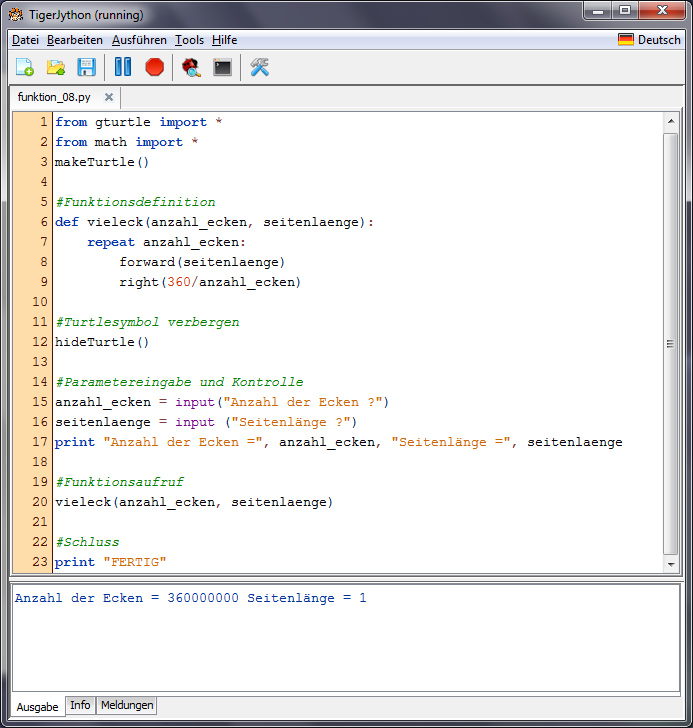
Code für das -Eck nach Hromkovič, J.; Kohn, T.: einfach Informatik – Programmieren, Klett, 2018, S. 47.
Das 2-Eck. 
Das e-Eck. 
