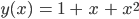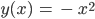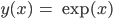Als Rike und Ben am Sonntag die Siegessäule besteigen und die Straße des 17. Juni und Unter den Linden bewundern, kommen ihnen diese beiden Straßen wie eine Turingmaschine mit einem unendlich langen Speicherband vor.
Rike Die Straße des 17. Juni zusammen mit Unter den Linden sind ja verdammt lang! Fast wie das Speicherband einer Turingmaschine!
Ben Das Brandenburger Tor als Lesekopf! Haha!
Rike Die Autos darauf könnten sich gut als Felder für Informationen eignen.
Ben Jaja, ist ja gut!
Rike Aber sag mal, ich habe gehört, alle Rechner sind zur Turingmaschine isomorph! Dann ist ja die Turingzeit noch lange nicht vorbei.
Ben Stimmt.
Rike Trotzdem kann ich mir nicht vorstellen, wie die Multiplikation in neuronalen Netzen von Zahlen mit boolschen Werten auf Gleitkommazahlen erweitert werden kann.
Levels in neuronalen Netzen
Ben Rike, stimmt, das geht etwas anders, und zwar so: Wir nehmen wieder Eingangsvektoren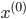 
und Datenverarbeitungen vom 
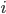-ten Level zum 
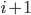-ten Level mittels
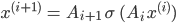
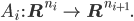
Die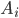 
’s sind affine Transformationen wie beim letzten Mal. 
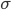soll jetzt das Produkt von Vektorkomponenten sein.
Rike Aha, jetzt sollen wir dem neuronalen Netz eine Methode geben, Gleitkommazahlen zu multiplizieren, wenn es die Multiplikation veränderlicher Größen nicht kennt.
Multiplikation in neuronalen Netzen
Ben Stimmt. Lin, Tegmark und Rolnick schlagen wieder einen Trick vor – und zwar zunächst nur für das Produkt zweier Gleitkommazahlen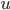 
und 
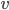. Nehmen wir mal:
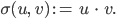
Das führen die Drei auf das Quadrat einer Funktion einer Veränderlichen zurück, Du brauchst also nur
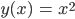
zu implementieren.
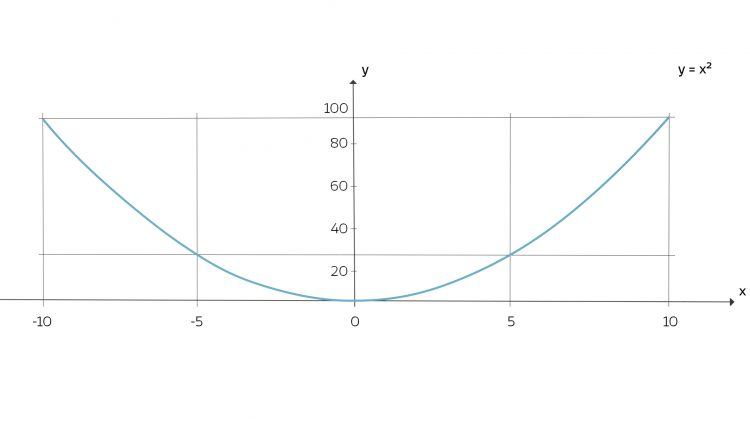
einer Veränderlichen zu implementieren – zum Beispiel das Quadrat einer Zahl.Rike Aha!
Algorithmus der Multiplikation
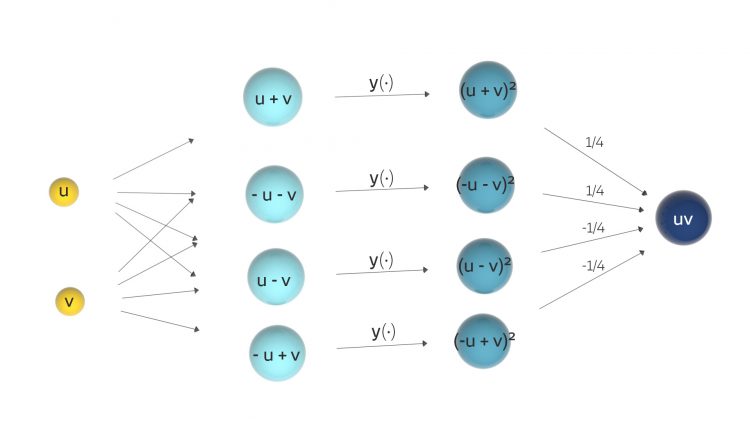
Ben Der Trick ist: Du quadrierst Summen und Differenzen von 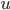und 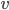, addierst und subtrahierst die Quadrate geschickt miteinander. Das können sogar Informatiker ausrechnen!
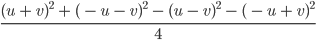
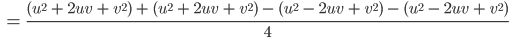
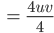
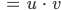
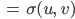
Rike Neuronale Netze mit binomischen Formeln!
Ben Klar, diese guten alten Sachen!
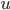und 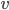.Rike Haha!
***
Übungsaufgaben
- Überprüfe, ob auch andere Funktionen statt des Quadrates in Frage kommen!
- Wenn ja, welche Funktionen könnten das sein?
Antworten
- Ja, es muss nur
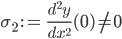. Dann muss man allerdings
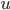und 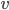mit einem Faktor 
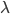skalieren, sodass 
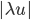und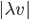 
klein werden: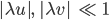
Und das daraus berechnete
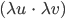noch durch den Faktor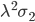
teilen.
- Zum Beispiel:
