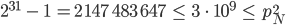Max hat nun endlich einen Job gefunden: In Berlin. Er ist Assistent der Geschäftsführung eines internationalen Konzerns im Medienbereich geworden. Vor kurzem ist er in eine kleine Wohnung gezogen. Lila hat sich für ein Studium in Deutschland entschlossen. Sie ist schon vor Semesteranfang nach Deutschland gekommen, um Deutsch zu lernen. Max hat Lila und Charly am Wochenende eingeladen. Sie sind an einem der Berliner Seen.
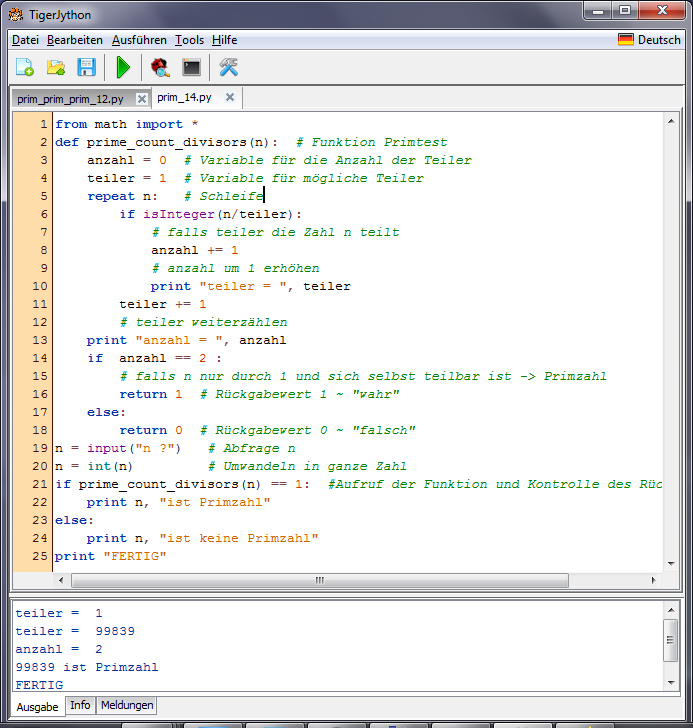
Charly erzählt von seinen Erfahrungen mit dem Programm TigerJython. So sollen die Kinder ein kleines Programm verstehen, dass die Anzahl der Teiler einer Zahl ermittelt. Durch Testen aller möglichen Teiler – von 1 beginnend bis eben zu dieser Zahl.
Teiler-Zählprogramm Hromkovič & Kohn
Max Hey, sag mal, sollen die Kinder die Zahl durch 1 teilen?
Charly Beim Lehrbuchbeispiel ist das so, 1 ist der erste Teiler und damit wird die Anzahl der Teiler erstmal 1.
Max Und als letztes wird durch die Zahl selbst geteilt?
Charly Ja!
Lila Für große Zahlen ist das ein unnötiger Rechenaufwand.
Charly Na gut, aber immerhin ist eine Zahl durch sich selbst teilbar. Jede Zahl hat mindestens 2 Teiler: 1 und sich selbst. Aber hört, mit diesen Kenntnissen und den nötigen Befehlen dazu werden die Kinder in einer Übungsaufgabe aufgefordert, einen “Befehl” zu schreiben, um für eine Zahl zu entscheiden, ob sie Primzahl ist oder nicht. [S. 87]
Max Charly, hast Du mal ein Flowchart für dieses Programm? Für mich als Medienproduzent wird das dann überschaubar.
Charly Das steht zwar überhaupt nicht auf dem Unterrichtsplan, aber das geht so:
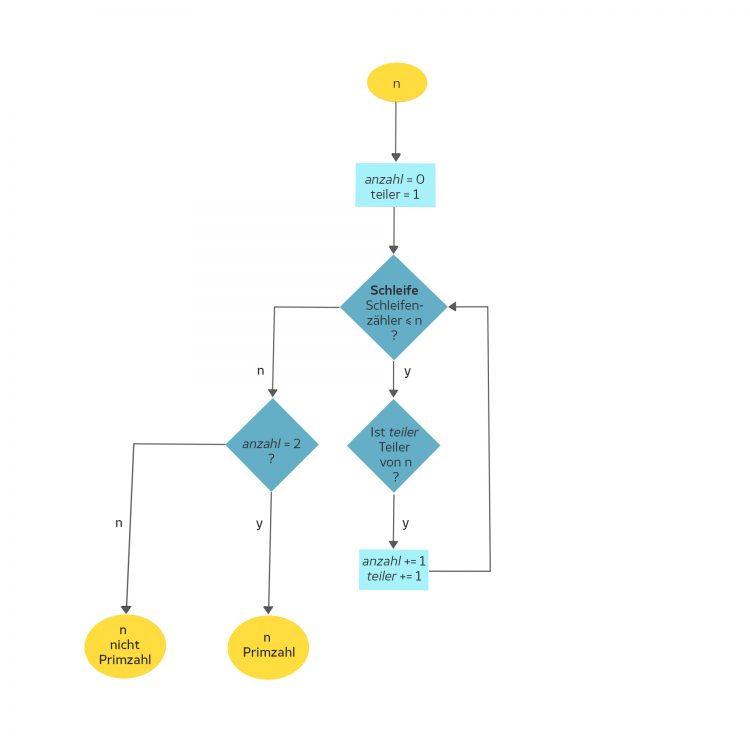
Max Verstehe. Aber ist die Primzahlsuche nicht eine schwierige Aufgabe aus der Kryptologie? Ist das nicht ein Forschungsthema weltweit? Das sollen die Kinder durch naives Herangehen lösen?
Charly Du hast recht! Für sehr große Zahlen ist das Vorgehen des Testens aller Teiler 1, 2, 3, 4, … zu langsam und zu uneffektiv. Ich habe das ausprobiert, ich habe dieses Teiler-Zählprogramm geschrieben – es hat meinen Rechner lahmgelegt. Ich war ziemlich wütend.
Lilas Prime Prime Program
Lila Es ist doch ganz einfach: Wenn eine Zahl durch 2 teilbar ist, ist sie keine Primzahl. Weitere Tests sind nicht nötig. Wenn eine Zahl nicht durch 2 teilbar ist, braucht die Teilbarkeit durch 4, 6, 8, 10, ... nicht überprüft werden. Ebenso mit der 3, der 5, der 7 ... You need to test only primes. Wie sagt man das deutsch?
Max Du brauchst nur die Primzahlen zu testen.
Lila Oh, Deutsch ist schwierig!
Primfaktorzerlegung
Max Lila, Du schaffst das. Dahinter steckt der Satz von der eindeutigen Primfaktorzerlegung. Charly, ist der denn bekannt?
Charly Nö! Aber den kann ich erklären! Jede Zahl lässt sich eindeutig in ihre Primfaktoren zerlegen, die 8 lässt sich als Zweierpotenz schreiben:
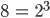
und die 909 als Produkt von 3² und 101:
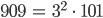
Aber, Lila, um die Primzahlen zu testen, brauche ich die Primzahlen!
Lila Right, doch die ersten Primzahlen bis 100 000 sind bekannt! Die kannst Du natürlich mit Deinem Teiler-Zählprogramm überprüfen, okay? Wenn die stimmen, dann nimmst Du die. Sobald eine Zahl durch eine Primzahl teilbar ist, ist der Test beendet. Wenn Du einen Teiler findest, der nicht 1 oder die Zahl selbst ist, bist Du fertig!
Max Ja, das ist gut. Dein Problem, Charly, war ja, dass die Zahl  auf a l l e Zahlen getestet wurde. Das sind
auf a l l e Zahlen getestet wurde. Das sind  Divisionen! Wenn Du nur die Primzahlen nimmst, die kleiner als
Divisionen! Wenn Du nur die Primzahlen nimmst, die kleiner als 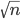 sind, dann sind das viel weniger.
sind, dann sind das viel weniger.
Charly Okay, wie kommst Du auf 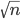 ?
?
Max Wenn eine Zahl durch 2 teilbar ist, dann hast Du den kleinsten und den größten nichttrivalen Teiler gefunden.
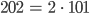
Charly Okay.
Max Wenn nicht, suchst Du immer weiter. Wenn Du der Reihe nach gehst, 2, 3, 5, … und keinen findest, dann wäre für den kleinsten Teiler 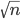 die letzte Chance. Zum Beispiel ist 121 nicht durch 2, 3, 5 … teilbar. Aber es ist
die letzte Chance. Zum Beispiel ist 121 nicht durch 2, 3, 5 … teilbar. Aber es ist
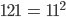
und 11 ist der größte von den kleinsten Teilern. 127 ist weder durch 2, 3, 5, 7 noch durch 11 teilbar, also ist sie Primzahl!
Charly Okay!
Flowchart
Lila Ich denke, das neue Prime Prime Program geht so:
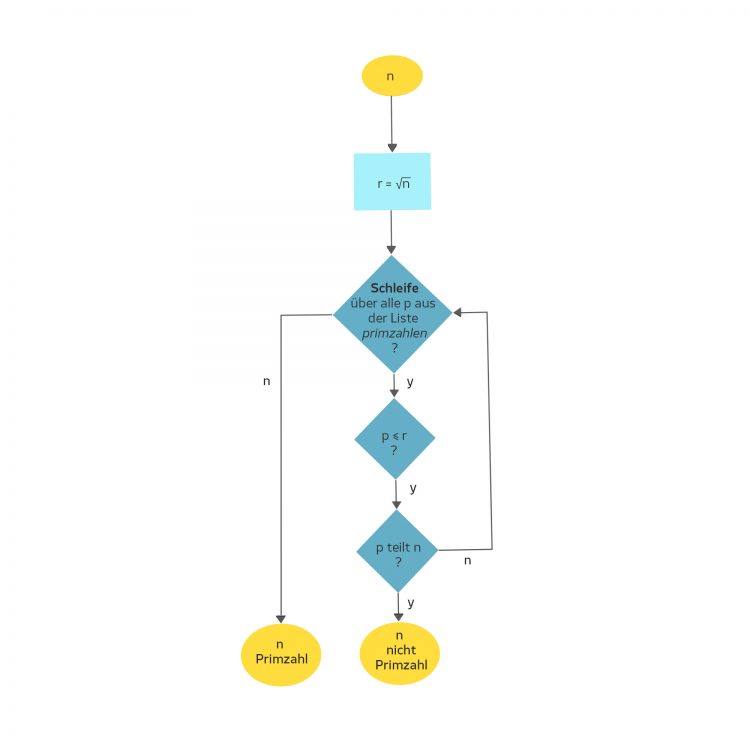
Charly Verstehe, ist sogar einfacher, gut so.
Code
Lila Gib mir mal Deinen Code, den können wir schnell modifizieren! Hier!
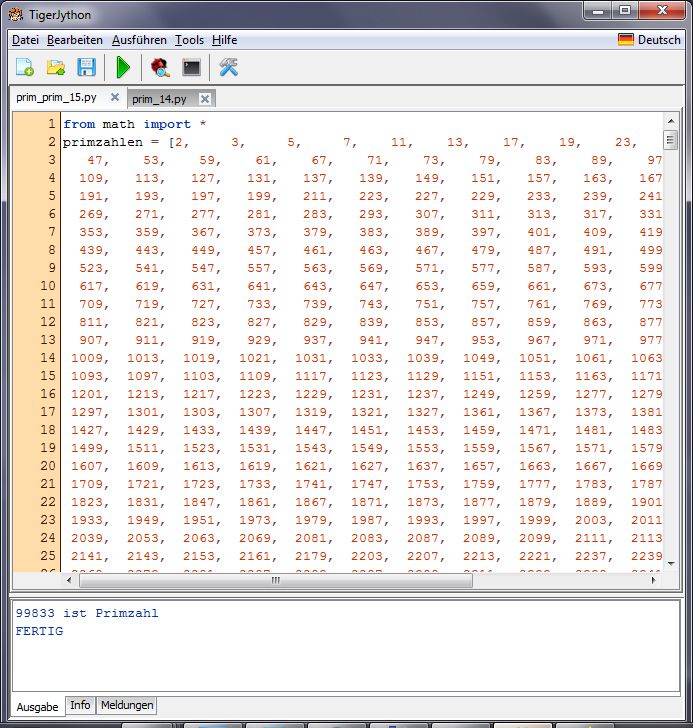
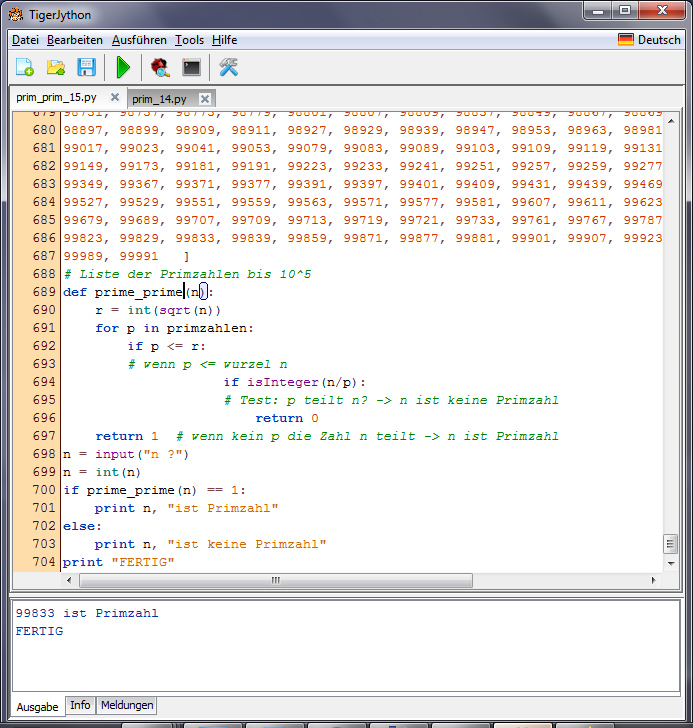
Programmtest
Lila Wollen wir mal die Mersenne-Zahlen testen?
Charly Sag doch mal eine!
Lila 23 - 1 !
Charly Sehr witzig! 7 ist Primzahl. Da brauche ich kein Programm.
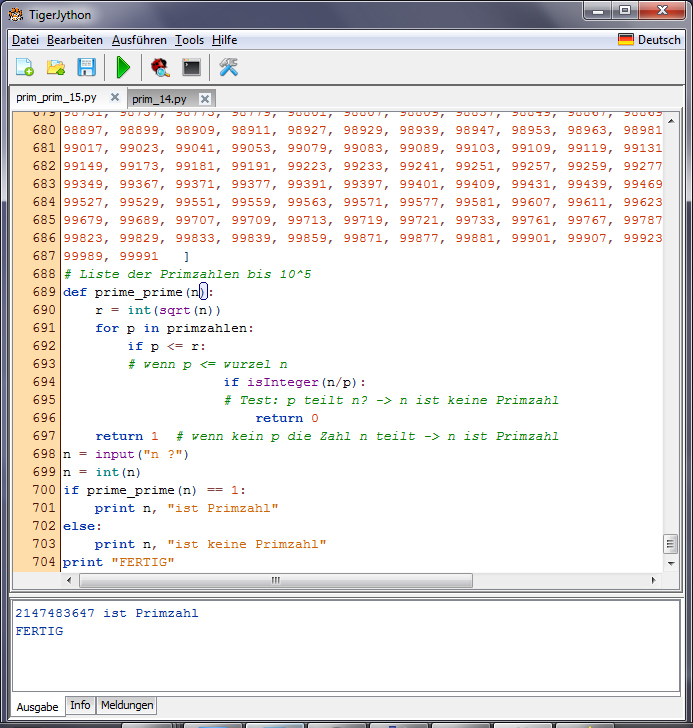
Lila Na gut, dann nimm doch mal 231 - 1!
Charly Hm, Dein Prime Prime Program ist aber schnell! 231-1 ist Primzahl! Lila, damit kann ich den Kindern gleich die Effektivität von Programmen erklären. Außerdem können wir Laufzeittests machen, beide Programme vergleichen und immer größere Primzahlen finden. Sehr gut!
Übungsaufgaben
- Wenn pN=99 991 die größte verfügbare Primzahl ist, für welche
 ist dann das Prime Prime Program korrekt?
ist dann das Prime Prime Program korrekt? - Ist das Ergebnis für 231 - 1 des Prime Prime Programs korrekt?
Lösungen
- Für
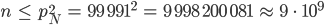
- Ja, es ist