Rike und Ben wollen gern mal Berlin von oben sehen. Fernsehturm? Aussichtsterrasse des Park Inn am Alex? Sie entscheiden sich für die Aussichtsterrasse.
Ben Boah, ist das schön! Die vielen Lichter! Was meinst Du, Rike, bilden die ein Muster?
Rike Naja, die meisten sind deterministisch angebracht und eingeschaltet.
Ben Rike, dann schreib‘ mir doch mal eine Formel dafür auf!
Rike Bist Du verrückt?
Ben Siehste, dann kann man das doch ganz gut mit dem Zufall simulieren. Ach, Rike, nenn‘ mir doch mal eine zufällige Zahl zwischen 1 und 10!
Rike 10
Ben Und noch eine?
Rike 10
Ben Und noch eine?
Rike 10
Ben Und noch eine, eine zufällige? Hast Du schlechte Laune?
Rike Hab keine Lust mehr!
Ben Rike, dann bist Du gerade durch den Zufallszahlentest von Knuth gefallen!
Rike Hab ich mir gedacht! Ich bin kein Zufallszahlengenerator! Hast Du denn einen coolen?
Die knuthschen Kongruenz-Methode
Ben Klar. Eigentlich liebe ich den einfachsten Algorithmus - die knuthsche Kongruenz-Methode. Die geht so:
Wenn wir gleichmäßig verteilte Zufallszahlen zwischen 1 und 10 haben wollen, nehmen wir
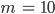
Du startest dann mit einer Anfangszahl X0 und wählst Zahlen a und c:
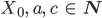
Die Zufallszahlen Xi kannst Du dann nach der knuthschen Formel berechnen:
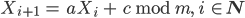
Rike Hört sich ganz einfach an! Ich nehme mal
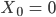
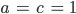
Dann kriege ich
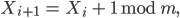
also
1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, ...

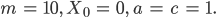
Wo ist denn da der Zufall?
Ben Erstmal ist das die Formel zur Berechnung, die ist wirklich einfach. Leider müssen ein paar Bedingungen erfüllt sein, damit diese Zahlen wirklich zufällig wirken.
Rike Ja, es wäre auch schön, wenn Außenstehende die Formel nicht erraten können. Hier sieht man zum Beispiel, dass sich die Ziffern nach 10 Zahlen wiederholen.
Ben Stimmt. Da haben wir das 1. Problem. Wir rechnen mit Restklassen. Wenn wir Zahlen zwischen 1 und 10 oder, was fast das Gleiche ist, zwischen 0 und 9 haben wollen, sollten wir m = 10 wählen, aber m ist gleichzeitig die Periode der Zufallszahlen. Für unseren Test ist sie viel zu klein!
Rike Hm.
Ben Aber das können wir ganz einfach lösen, wir nehmen eine große Periodendauer m und machen eine kleine zusätzliche Rechnung und berechnen aus den Zufallszahlen von 0 bis m-1 welche von 0 bis 9.
Rike Okay. Welche Bedingungen gibt es denn?
Ben Warte mal, ich muss das nachschauen,…, hier,
Theorem A
Die lineare Kongruenzfolge hat die Periode m genau dann, wenn die drei Bedingungen erfüllt sind:
(a) c ist teilerfremd zu m
(b) b = a - 1 ist Vielfaches von jeder Primzahl p, die m teilt
(c) b ist Vielfaches von 4, wenn m Vielfaches von 4 ist.
Knuth schreibt, dass die Ideen dazu schon 100 Jahre alt sind und schließlich 1962 bewiesen worden. Das kannst Du ja mal nachprüfen. Welche Periode wollen wir wählen?
Rike Na, 1000 Zufallszahlen hätte ich schon gerne.
Ben Okay, man nimmt für m gern 2er Potenzen, lass uns mal
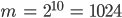
nehmen.
Rike Ja, gut, das ist gleich die Primfaktorzerlegung. Außerdem ist m durch 4 teilbar. Dann muss b durch 4 teilbar sein. Die Bedingung (b) ist dann gleich mit erfüllt. b könnte 4, 8, 12, … sein. Für c könnten wir jede ungerade Zahl wählen.
Ben Gut. Eben hatten wir schlechte Erfahrungen mit kleinen Zahlen 0 und 1. Lass uns a und c so wählen, dass sie Primzahlen sind.


Okay?
Rike Gut, ich schlage dann
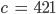
vor.
Ben Und ich nehme
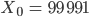
Rike Okay! Lass mich das mal ausrechnen:
848, 181, 726, 643, 588, 897, ...
Ben Schön. Wollen wir für die Zufallszahlen zwischen 0 und 9 einfach die Hunderterstelle nehmen? Also
8, 1, 7, 6, 5, 8, ...
Kannst Du das ausrechen?
Rike Klar, hier schau mal:

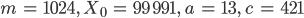 und einer "Nachrechnung"
und einer "Nachrechnung"Erwartungswert und Varianz
Okay, gefällt mir. Wie ist denn der Erwartungswert? Warte:
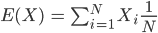
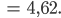
Ben Und die mittlere Abweichung davon?
Rike Die Varianz? Die ist
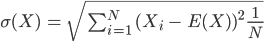
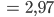
Ben Ich find's toll! Obwohl es einige Kritik an dem Algorithmus gibt, habe ich ja immer noch die volle Kontrolle. Die Zahlen von 0 bis 9 sind relativ gleichmäßig verteilt, es bildet sich kein periodisches Muster. Natürlich ist m = 1024 noch etwas klein. Kannst Du mal eine Standard-Zufallsfunktion aufrufen? Eine, die mit dem Mersenne-Twister-Verfahren berechnet wurde?
Vergleich mit dem Mersenne-Twister-Verfahren
Rike Klar, kann ich machen, mit
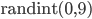
in Phyton und der Wahl einer Anfangszufallszahl:
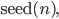
die verrate ich aber nicht!, kriege ich 1000 Zufallszahlen:

Ben Was kriegst Du für den Erwartungswert?
Rike
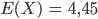
Ben Und die Varianz?
Rike
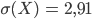
Vergleich mit der Gleichverteilung
Ben Schön, für eine Gleichverteilung der Zahlen 0 bis 9 kriegen wir den Erwartungswert
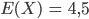
und eine mittlere quadratische Abweichung von
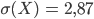
Das passt ja schon ganz gut. Mein Lieblingsalgorithmus hat das fast so gut wie der Twister gemacht!
Rike Sag Du mir doch mal eine Zufallszahl von 1 bis 10?
Ben Hahaha.
***
Übungsaufgabe
Vergleiche die beiden Verfahren an Beispielen!
