Lila lebt sich in Berlin ein und besucht ihren Deutsch-Kurs. Heute Abend war eigentlich Kino vorgesehen, aber Max muss einen prominenten Gast seiner Firma betreuen. So geht Lila allein nach Hause. Sie hat von Charly die TigerJython-Files bekommen und schaut sie beim Nachhauseweg an. Als sie am Dönerladen vorbeikommt, ruft ein Mitarbeiter die fertigen Bestellungen aus:
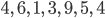
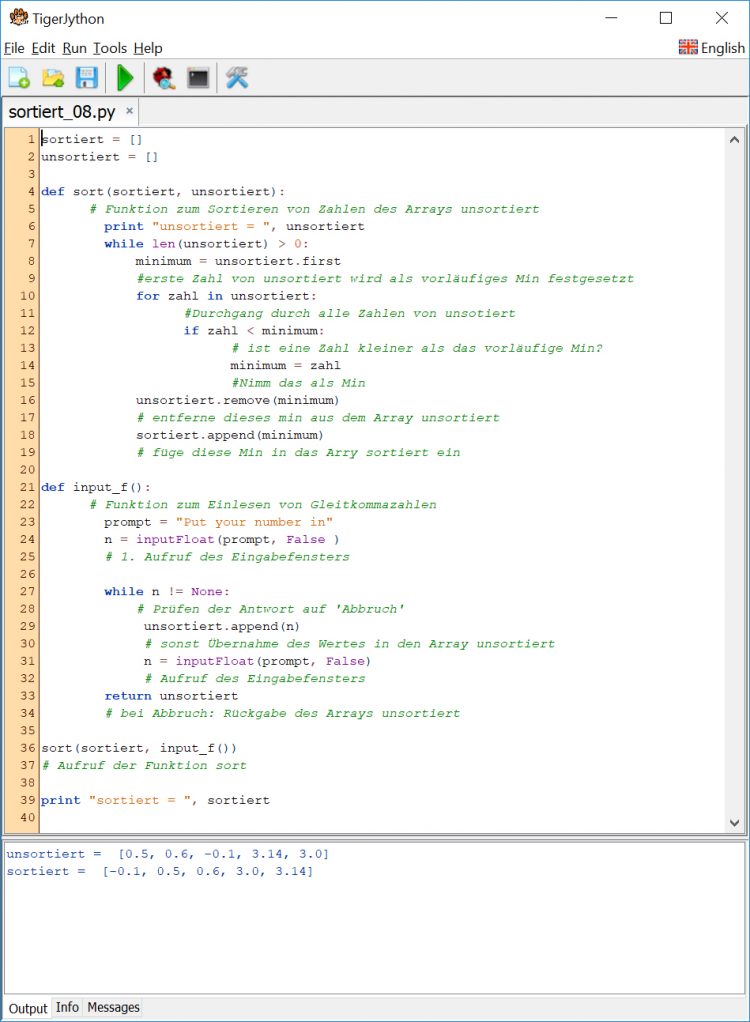
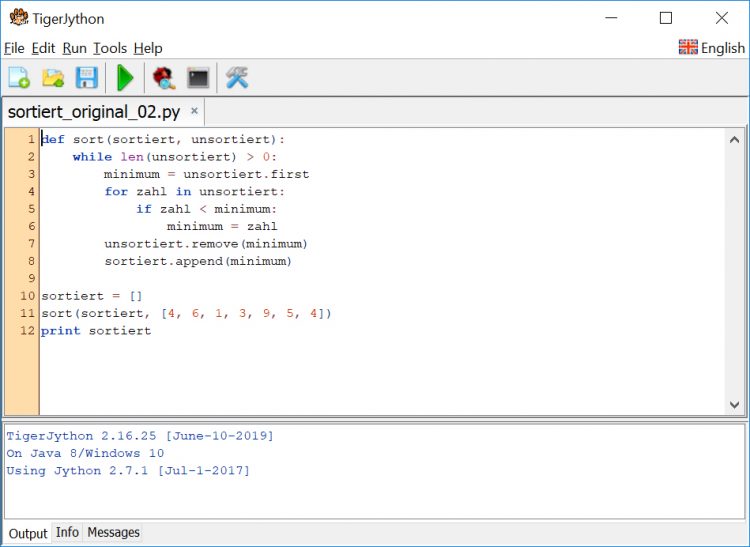
Komisch, genau die kommen im Sortieralgorithmus vor. Sie studiert gerade ein Programm, das genau diese Zahlen der Größe nach sortiert:
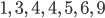
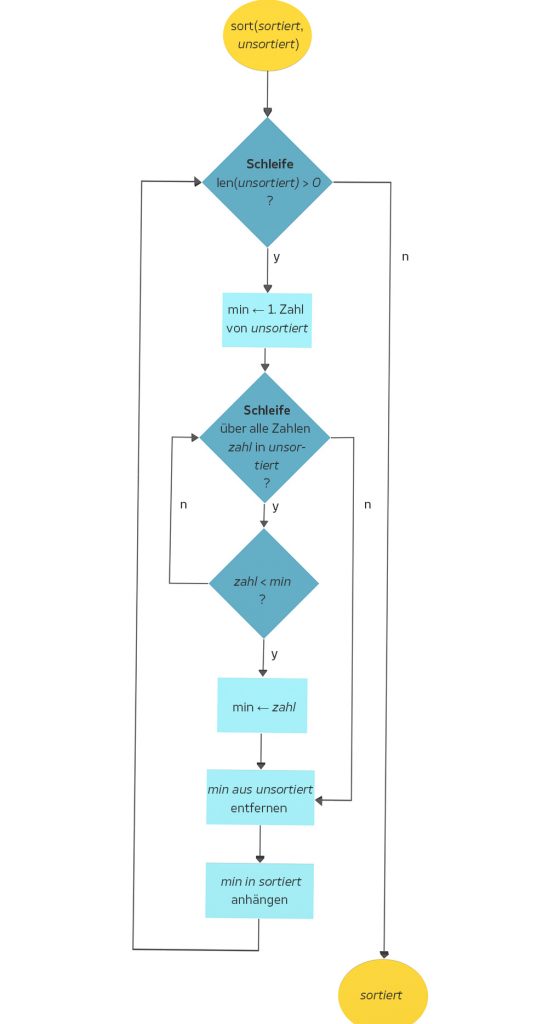
Vielleicht steckt ein Zauber dahinter? Sie weiß es nicht. Schade, sie würde gern Max dazu fragen. Der Algorithmus „im Buch“ gefällt ihr wirklich. Er geht so:
Sortieralgorithmus
Man legt ein Array unsortiert fest:
Man vereinbart ein Array sortiert, in das nacheinander die kleinsten Zahlen von unsortiert hineingeschrieben werden.
1. Schleife
(A) Zuerst bestimmt man die Länge von unsortiert:
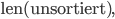
das ist die Anzahl der Elemente, also
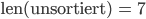
Ist die Länge größer als 0, macht man weiter. Um die kleinsten Zahlen systematisch zu finden, fängt man mit der 1. Zahl von unsortiert an:
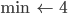
2. Schleife
(B) Man geht alle Stellen von unsortiert durch und fragt, ob eine kleiner als 4 ist. Ja, es ist
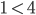
Dann ersetzt man das Minimum durch diese Zahl, sonst bleibt sie:
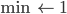
Aus unsortiert wird das Minimum herausgenommen,
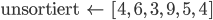
in sortiert wird es angehängt:
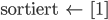
Mit diesen beiden Arrays geht man zu (A) und macht das erneut. Lila fragt sich, warum die Schüler in Deutschland kein Flowchart lernen, das wäre doch anschaulich, das gehört doch zum Programmieren dazu, auch Donald Knuth schreibt solche Flowcharts.
Problem
Doch nun will sie keine feste Folge im Programm benutzen, sondern interaktiv was eingeben. Doch als sie das ausprobiert, klappt das nicht. Hauptschuld daran hat die Art der Datentypen in TigerJython – nämlich alles offen zu lassen. So kann sie mit dem im Buch empfohlenen Befehl
- Zeichenketten
- ganze Zahlen
- durch Komma getrennte Zahlen
- Dezimalzahlen mit Dezimalpunkt
- Sonderzeichen
eingeben. Doch eigentlich will sie nur ganze und Gleitkommazahlen zulassen. Und schlimmer noch, wenn sie so eine wiederholte Eingabe zulässt, wenn sie eine Schleife macht mit beliebig vielen Eingaben, wie beendet man dann die Eingabe, wenn jede Eingabe akzeptiert wird und „Abbrechen“ zum Abbruch des Programms führt?
Sie verzweifelt fast. Dann findet sie 2 Befehle:
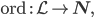
für
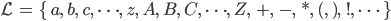
als Menge aller eingebbaren Zeichen einer Tatstatur und den Befehl

die ihr brauchbar erscheinen. Doch der 1. Befehl wandelt alle Buchstaben u.ä. Zeichen in eine natürliche Zahl – nur Zahlen sind als Eingabe nicht zugelassen! Und der 2. Befehl wandelt alle ganzen Zahlen in Buchstaben oder Zeichen um, lässt aber als Eingaben keine Elemente von 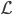 zu. Wie soll sie vor der Eingabe wissen, welche Eingabe kommt? Doch sie will nicht aufgeben. Es muss doch möglich sein, mit fehlerhaften Eingaben umzugehen – ohne Absturz des Programms. Warum spielt das eigentlich im Schulbuch keine Rolle? Geben alle Kinder in Deutschland nur korrekte Werte ein?
zu. Wie soll sie vor der Eingabe wissen, welche Eingabe kommt? Doch sie will nicht aufgeben. Es muss doch möglich sein, mit fehlerhaften Eingaben umzugehen – ohne Absturz des Programms. Warum spielt das eigentlich im Schulbuch keine Rolle? Geben alle Kinder in Deutschland nur korrekte Werte ein?
Ein spezieller Eingabebefehl
Doch endlich kommt Max. Zusammen finden sie eine Liste aller TigerJython-Befehle im Netz. Das kann Max wirklich gut. Einer davon ist geeignet, er sieht ein bisschen kompliziert aus, aber zusammen verstehen sie den:

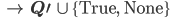
Dabei bezeichnet 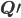 die Gleitkommazahlen.
die Gleitkommazahlen. 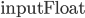 ist eine Funktion, die ganze und Gleitkommazahlen in Gleitkommazahlen umwandelt:
ist eine Funktion, die ganze und Gleitkommazahlen in Gleitkommazahlen umwandelt:
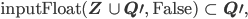
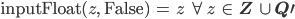
Bei Buchstaben u.a. Zeichen gibt sie eine Fehlermeldung aus:
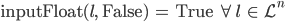
Außerdem hat sie eine weitere Option True oder False für den Abbruch. Bei „Abbruch“ wird nur die Eingabe beendet, so wie Lila sich das wünscht, und das Programm wird weiter ausgeführt.

Jetzt muss Lila das nur noch geschickt anwenden und mit dem Sortierprogramm „verknüpfen“.
***
Übungsaufgaben
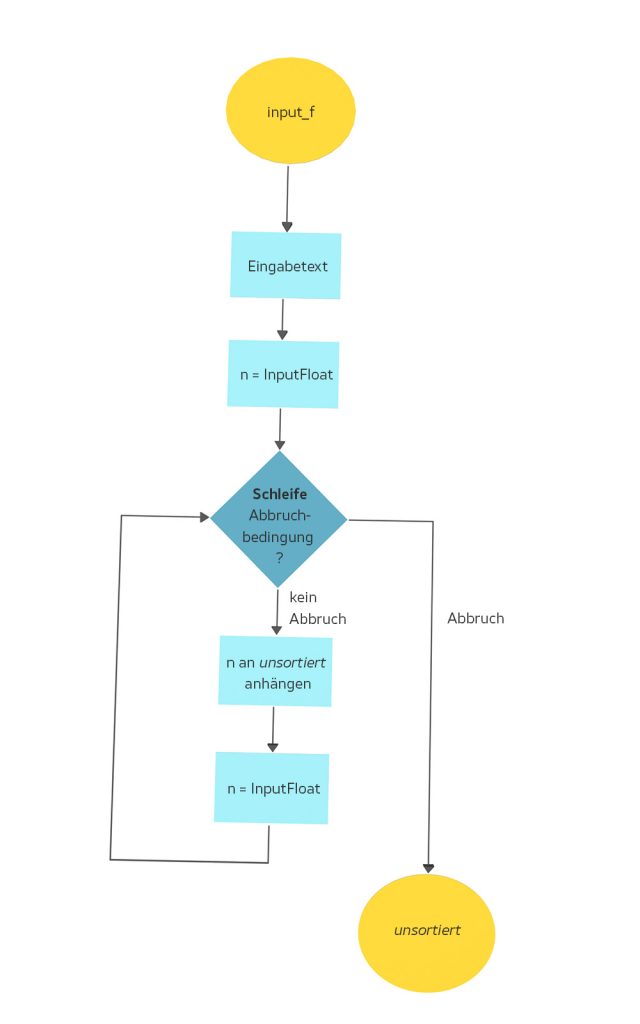
- Schreibe ein Flowchart für so eine Eingabe-Funktion!
- Schreibe den Code für den Sortieralgorithmus mit allgemeiner Eingabe!
Lösungen