Ben und Rike gefällt es in Berlin. Ihre Wohnung im Hinterhaus ist bezahlbar, hier bleiben sie. Ben richtet eine kleine Kochecke ein und bringt Kacheln an. Dazu hat er ein Muster gezeichnet und die Abstände fixiert. Doch am Ende sieht so eine Küche in der Altbauwohnung nicht wie eine Designerküche aus. Irgendwie ist nicht alles so rechtwinklig geworden wie geplant. Rike bewundert lachend Bens Werk.
Rike Hahaha, was hast Du denn gemacht? Sieht wirklich realistisch aus, nicht wie im Fernsehfilm!
Ben Sehr witzig! Habe mir echt Mühe gegeben! Aber was meinst Du?
Rike Weißt Du, häufig erkennt man computergenerierte Bilder daran, dass sie zu perfekt sind. Alles sieht wie am Reißbrett entworfen aus, nirgendwo im Bild ist das echte Leben, alles ist perfekt.
Ben Na, gut.
Rike Aber schau mal, das ist gerade auch unser Problem bei der Analyse von Bildern. Wenn man schnell erkennt, dass ein Bild computergeneriert ist, müssen wir daran arbeiten, die computergenerierten Bilder besser zu machen.
Ben Okay?
Standard-CG-Lösung
Rike Schau mal, wenn man mal das Bild von Kacheln nimmt, dann sieht das mit Standard-CG-Methoden erzeugte Bild so aus:
Aber ein realistisches sieht ganz anders aus. Die Kacheln sind unregelmäßig verteilt.
Kacheln mit Normalverteilung
Ben Was soll‘s, man nehme die gute alte Normalverteilung – und fertig!
Rike Okay, ich probiere das mal aus. Zuerst würde ich die Kacheln nur drehen, sonst kriegen wir zu viele Freiheitsgrade. Und da würde ich Drehungen nur bis zu einer Grenze zulassen. Beim Fotografieren beobachte ich das auch, Drehungen bis 1° sind kaum wahrnehmbar, aber 5° wäre für mich das Maximum an Störung des Regelmäßigen. Drehungen in beide Richtungen, also von -5° bis +5° würde ich zulassen – oder die anderen als sehr, sehr unwahrscheinlich zulassen.
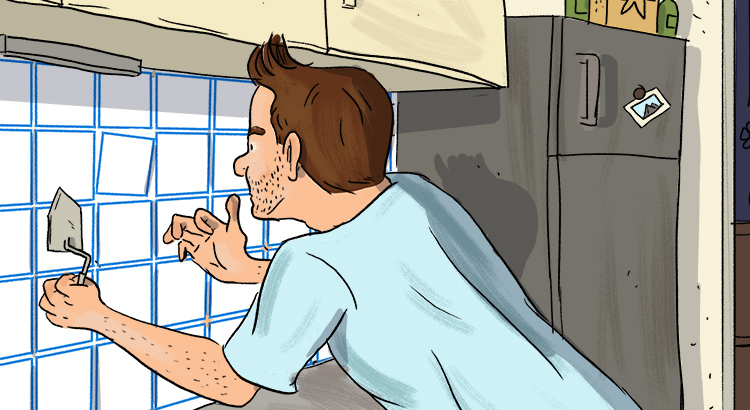
Ben Okay, dann hast Du eine symmetrische Verteilung um 0. Dein zugelassenes Maximum von 5° sind im Bogenmaß 0,09. Was hältst Du von einer Varianz von
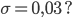
Rike Okay. Die Wahrscheinlichkeitsdichte sieht dann so aus:
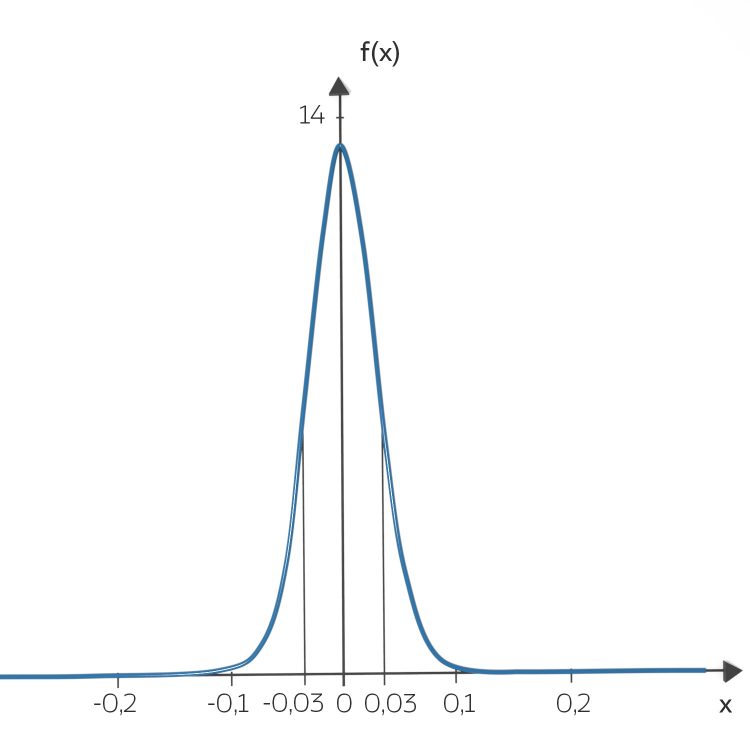
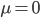 und
und 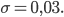
Dann berechne ich eben die Wahrscheinlichkeiten für das Auftreten der Drehungen für bestimmte Winkel, warte...
| Drehung um den Winkel in ° | Drehung um den Winkel im Bogenmaß | Anzahl der Kacheln von 100 |
| -0,5 – 0,5 | -0,009 – 0,009 | 23 |
| 0,5 – 1,5 | 0,009 – 0,026 | 19 |
| 1,5 – 2,5 | 0,026 – 0,044 | 11,5 |
| 2,5 – 3,5 | 0,044 – 0,061 | 5 |
| 3,5 – 4,5 | 0,061 – 0,079 | 1,5 |
| 4,5 – 5,5 | 0,079 – 0,096 | 0,5 |
Ben Okay, wenn wir die negativen Winkel dazu nehmen, komme ich auf eine Summe von 98. Nicht schlecht!
Rike Das Bild sieht dann so aus:

Ben Okay!
Rike Ich finde es nicht gut! Zu viele Kacheln wirken unverändert, und die eine Kachel, die ich um die 5° gedreht habe, wirkt als Point of Interest! Damit ist ganze Wirkung einer händischen, realistischen Arbeit hin!
Ben Nagut, war ja nur ein Versuch! Was gibt’s denn noch?
Kacheln mit der Dreiecksverteilung
Rike Na, vielleicht die Dreiecksverteilung?
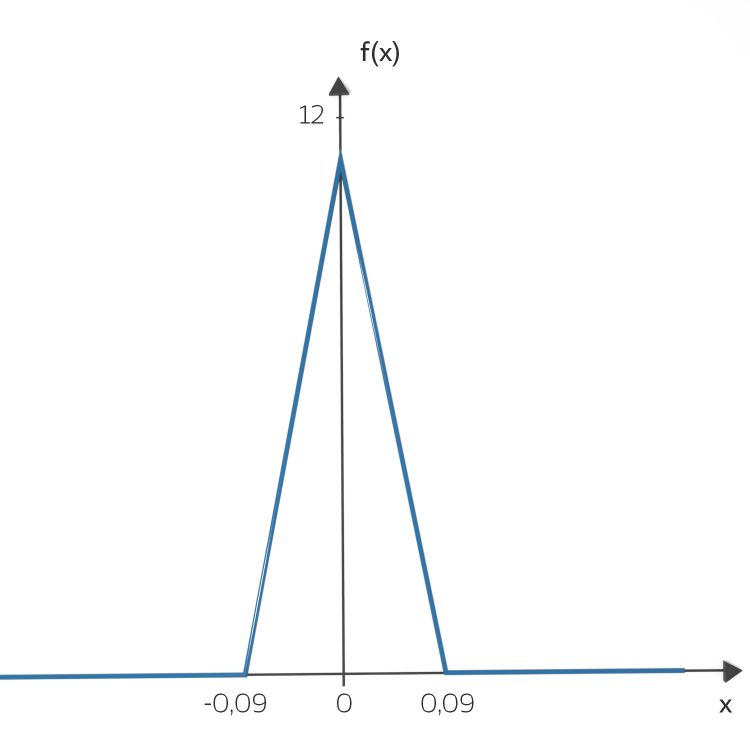
 nicht Null, nur sehr klein.
nicht Null, nur sehr klein.Wahrscheinlichkeitsdichte der Dreiecksverteilung von -5° - + 5°
Ben Ja, gut, das Phänomen mit den wenigen Drehungen bei 5° und den zu vielen Drehungen bei 0° ist dann abgeschwächt.
Rike Richtig, ich kriege dann die Werte:
| Drehung um den Winkel in ° | Drehung um den Winkel im Bogenmaß | Anzahl der Kacheln von 100 |
| -0,5 – 0,5 | -0,009 – 0,009 | 18 |
| 0,5 – 1,5 | 0,009 – 0,026 | 16 |
| 1,5 – 2,5 | 0,026 – 0,044 | 12 |
| 2,5 – 3,5 | 0,044 – 0,061 | 8 |
| 3,5 – 4,5 | 0,061 – 0,079 | 4,5 |
| 4,5 – 5 | 0,079 - 0,096 | 1 |
Das Kachelbild sieht so aus:

Ben Nicht schlecht!
Rike Aber weißt Du, was noch viel besser ist?
Ben Wahrscheinlichkeit ist nicht so mein Ding, bisher habe ich alles mit der Normalverteilung gelöst.
Kacheln mit der Gleichverteilung
Rike Na, die Gleichverteilung!
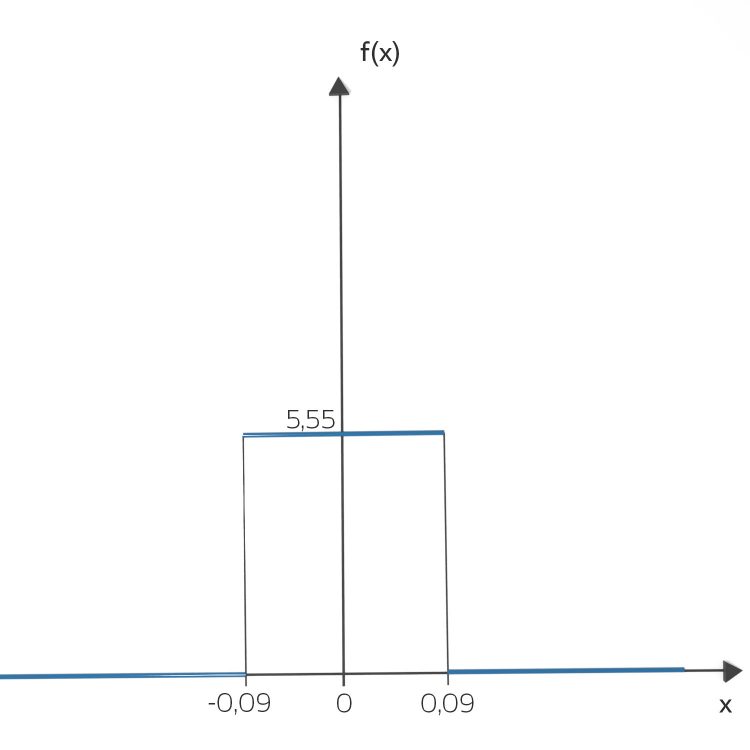
Hier lassen sich die Wahrscheinlichkeiten sofort aufschreiben:
| Drehung um den Winkel in ° | Drehung um den Winkel im Bogenmaß | Anzahl der Kacheln von 100 |
| 0 – 1 | 0 – 0,017 | 10 |
| 1 – 2 | 0,017 – 0,035 | 10 |
| 2 – 3 | 0,035 – 0,052 | 10 |
| 3 – 4 | 0,052 – 0,070 | 10 |
| 4 – 5 | 0,070 – 0,087 | 10 |
Und das Bild

gefällt mir am besten!
Ben Mir auch!
Übungsaufgaben
- Überprüfe die berechneten Wahrscheinlichkeiten!
- Hat die Gaußsche Normalverteilung nicht doch noch eine Chance?
- Diskutiere die einzelnen Bilder! Warum gefällt Rike das letzte so gut?
Lösung
2. Bei einer größeren Varianz sind die Werte für die Drehungen breiter verteilt, allerdings gibt es dann auch ganzzahlige Werte über 0 bei bei Winkeln über 5° (und unter -5°): Für
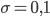
ergibt sich:
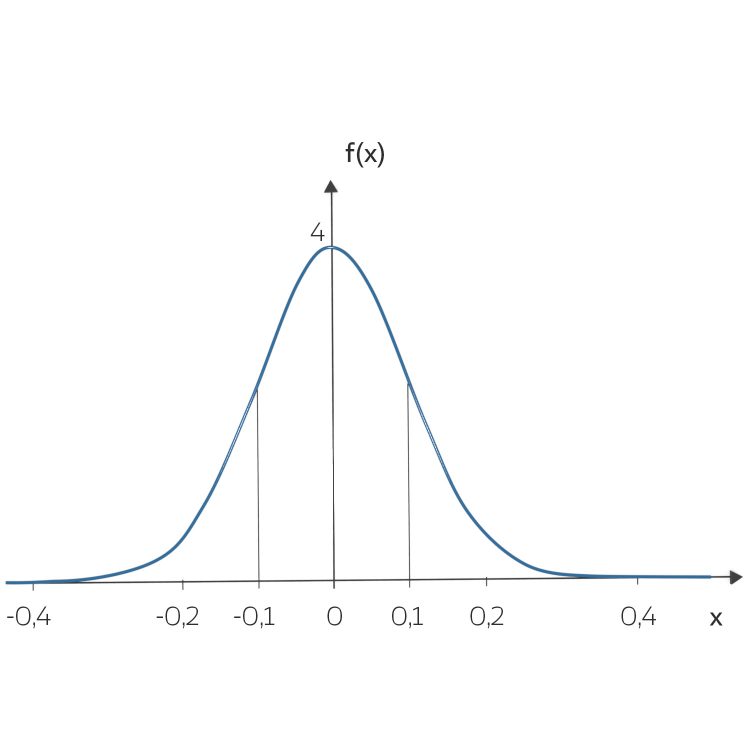
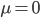 und einer größeren Varianz von
und einer größeren Varianz von 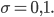
| Drehung um den Winkel in ° | Drehung um den Winkel im Bogenmaß | Anzahl der Kacheln von 100 |
| -0,5 – 0,5 | -0,009 – 0,009 | 7 |
| 0,5 – 1,5 | 0,009 – 0,026 | 7 |
| 1,5 – 2,5 | 0,026 – 0,044 | 7 |
| 2,5 – 3,5 | 0,044 – 0,061 | 6 |
| 3,5 – 4,5 | 0,061 – 0,079 | 5 |
| 4,5 – 5,5 | 0,079 - 0,096 | 5 |
| 5,5 – 6,5 | 0,096 - 0,113 | 4 |
| 6,5 – 7,5 | 0,113 - 0,131 | 3 |
| 7,5 – 8,5 | 0,131 - 0,148 | 3 |
| 8,5 – 9,5 | 0,148 - 0,166 | 2 |
| 9,5 – 10,5 | 0,166 - 0,183 | 2 |
| 10,5 – 11,5 | 0,183 - 0,201 | 1 |
| 11,5 – 12,5 | 0,201 - 0,218 | 1 |
| 12,5 – 13,5 | 0,218 - 0,236 | 0,5 |