Ben bereitet sich auf den nächsten Vortrag vor. Er soll neuronale Netze erklären. Dazu nimmt er ein Foto von Rikes Katze Molly, zerlegt es in kleinste Teile und will zeigen, wie man mit neuronalen Netzen wieder eine Katze herausbekommt. Doch irgendwas klappt nicht.
Bens Problem
Rike Hi Ben, so hab‘ ich Dich ja noch nie gesehen. Was ist los?
Ben Hi Rike, ich komme mit meinem Vortrag über neuronale Netze nicht weiter. Ich nehme mal ein Bild, lass uns mal das von Deiner Katze nehmen.
Rike Okay!
Ben Es hat, hm, warte mal, 2128 x 1416 Pixel. Stell Dir vor, Du bekommst sie alle einzeln und sollst daraus wieder Deine Katze verifizieren.
Rike Oh!
Ben Dann nehmen wir die
2128 x 1416 = 3 013 248 Pixel
und sortieren die.
Rike Nach welchem Kriterium?
Ben Nach Farben.
Rike Gut. Dann kriegen wir nicht so viele verschiedene. Molly ist ja ziemlich einfarbig, sie hat nur ‘nen weißen Bauch.
Ben Aber im Foto gibt es Helligkeitsverläufe und „Kanten“. Die versuche ich herauszufinden.
Rike Okay, aber aus einer Tabelle mit verschiedenen Farben und Anzahlen dazu kannst Du niemals sicher eine Form rekonstruieren!
Ben Stimmt! Wir müssen das anders machen! Dann lass uns die nächste sinnvolle Einheit nehmen: 4er Pakete!
Kleinste sinnvolle Strukturen
Rike Gut! Da hast Du Strukturen drin. Statt 3 013 248 Pixel hast Du nur noch 753 312 Pakete. Und da suchst Du bestimmt solche Strukturen:
1. Einfarbig
2. Kante rechts
3. Kante links
4. Kante unten-oben
5. Kante oben-unten
6. Kante oben
7. Kante unten
8. Ecke rechts unten
9. Ecke rechts oben
10. Ecke links oben
11. Ecke links unten
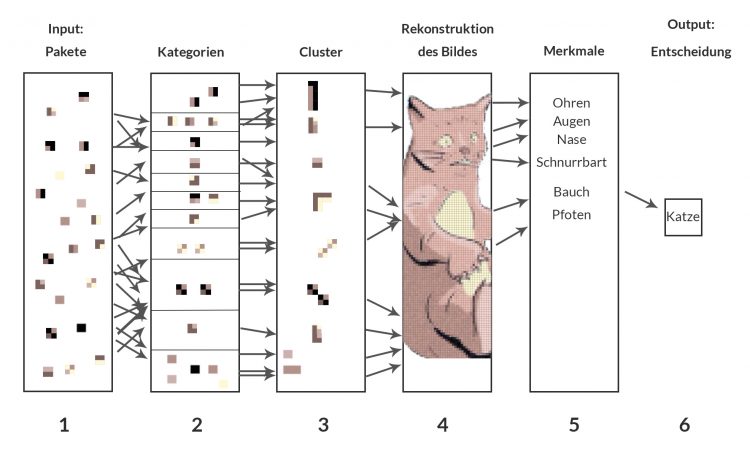
Ben Ja, das ist gut. Ich sortiere alle Pakete in diese 11 Kategorien und behalte die Information jedes Paketes. Da steckt ja noch die Farbigkeit drin.
Katzen-Leveldesign
Rike Gut.
Ben Das ist der zweite Layer. Jetzt versuche ich, aus den Farbinformationen Cluster zu bilden, zum Beispiel aus einfarbigen Paketen größere Flächen zusammenzusetzen. Und natürlich Kanten zusammenzusetzen.
Rike Da ist ein ziemliches kombinatorisches Problem!
Ben Ja, als nächstes versuche ich, die Cluster zusammenzusetzen.
Rike Gut!
Ben Dann kommt eine Art Mustererkennung dran. Ich versuche, Ohren, Augen, Nase, Schnurrbart, Bauch und Pfoten zu zählen und zu identifizieren.
Rike Okay!
Ben Und dann finde ich heraus, dass es eine Katze ist. Wenn es nicht gut läuft, finde ich gar nichts heraus!
Rike Sag mal, dann hast Du jetzt 6 Levels? Von einem zum nächsten machst Du immer lineare Transformationen und danach so eine Art Entscheidung, richtig?
Ausblick
Ben Stimmt. Diese Levels kann man als eine Art Abstraktion sehen. An dieser Stelle fangen die ganzen theoretischen Überlegungen an, wie viele Level es gibt. Mehrere Levels bilden ein deep network, flache – mit nur einem Level – nennt man shallow.
Rike Dann hast Du jetzt ein tiefes neuronales Katzennetz entworfen?
Ben Ja!
Rike Wo kommt eigentlich der Name neuronales Netz her?
Ben Das ist historisch entstanden, man sucht immer Analogien zum menschlichen Gehirn. Die tatsächlichen Werte des Inputs heißen Neuronen. Man stellt die Neuronen im Netz gerne grafisch dar, das sieht so „neuronal“ aus und manchmal gibt es im neuronalen Netz „tote Enden“.
Rike Hahaha.
***
Übungsaufgabe
Kann es bei diesem Layout "tote Enden" geben?
Lösung
Ja, beispielsweise kann ein Cluster der Art

nicht sicher in eine der 11 Strukturen klassifiziert werden.
Oder wenn ein Originalcluster der Art Kante unten-oben
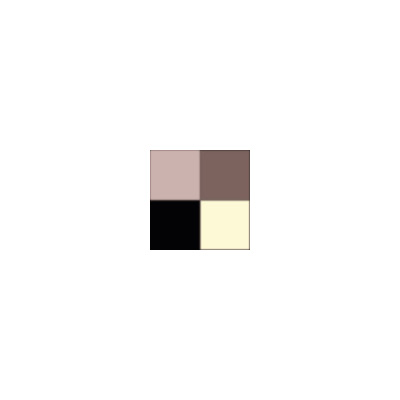
unscharf fotografiert wird

, sodass neue Farben entstehen, die nicht in der Farbpalette sind.










