Charly ist am Wochenende wieder nach Berlin gekommen und besucht Max. Halberfroren kommt er in Max‘ Wohnung an.
Max Hi Charly, komm rein! Wie geht’s?
Charly Max, schön, wieder in Berlin zu sein, schön warm hast Du's hier! Mir geht's gut, aber …
Max Aber?
Charly Ich hab‘ ein Problem. Ich habe so 'ne blöde Matheaufgabe im Lehrplan, dass ich mit meinem Gewissen kämpfen muss. Ich weiß nicht weiter, wie ich damit umgehe.
Max Na, erzähl mal!
Charly Die Aufgabe geht so:
Die Eiszeitberechnungsaufgabe
Die Änderungsrate der Masse eines Alpengletschers wird beschrieben durch die Funktion:
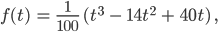
t ... Zeit in Monaten
f ... in 1000 m3
Zum Zeitpunkt
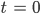
hat der Gletscher eine Masse von
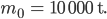
Es soll das zeitliche Verhalten des Gletschervolumens berechnet werden. Es soll nachgewiesen werden, „dass die Gletschermasse über die Jahre stabil ist.“
Max Okay. Wie löst Du das?
Charlys Herleitung
Charly Ich nehme x(t) für das zeitliche Verhalten der Gletschervolumens und erhalte die Lösung mit Integration:
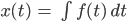
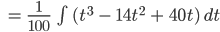
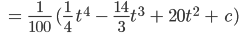
Diskussion des Anfangswertes
Außerdem habe ich ja einen Anfangswert für x(t) zur Zeit t = 0:
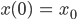
Dazu muss ich nur den Anfangswert von 10 000 t in Kubikmeter umrechnen, die Gletscherdichte ist leider nicht gegeben, das muss (im Unterricht) via Internet erfragt werden. Das ist die gute Seite an der Aufgabe, alle dürfen ihr Handy rausholen. Doch dann stellt sich gleich auf der Wikipedia-Seite heraus, dass man von einem Gletscher spricht, wenn er mindestens 30 m hoch ist und 0,1 km2 Grundfläche hat.
Bei einer Dichte von
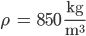
komme ich auf den Anfangswert von
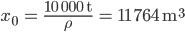
Wenn dieser „Ausgangsgletscher“ 30 m hoch ist, dann hat er eine Fläche von
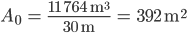
Wenn der Gletscher kastenförmig wäre, hätte er eine Seitenlänge von ca. 20 m.
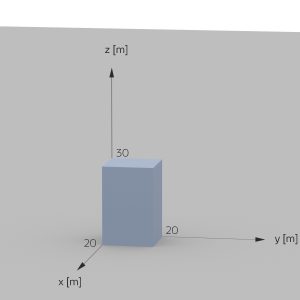
Max Hey, solche Gletscher gibt es in den Alpen gar nicht! Das sind ja Eissäulen! Haha!
Charly Die Autoren der Aufgabe haben wohl übersehen, dass ein Gletscher eine Mindestgröße der Grundfläche von 0,1 km2 hat. Das sieht doch ganz anders aus:
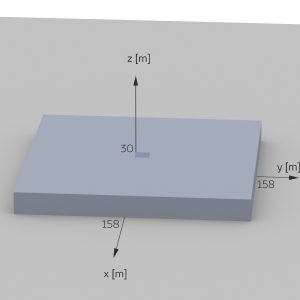
Max Stimmt!
Lösung der DGL mit Anfangswert
Charly Jetzt muss ich nur noch den Anfangswert in die Lösung x(t) einsetzten, um die Integrationskonstante zu bestimmen.
Max Klar.
Charly Mit
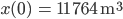
eingesetzt in

kriege ich
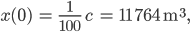
also
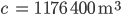
und schließlich
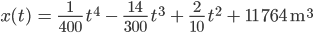
Max Okay, gut.
Lokale Minima und Maxima der Lösung
Charly Jetzt soll ich die Minima und Maxima bestimmen. Dazu leite ich x(t) ab:
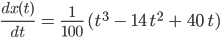
Max Okay, verstehe, das hatte ich auch mal vor langer Zeit! Das musst Du nun zu Null setzen, warte mal, das kann ich auch! Den Faktor lassen wir weg, dann kriegen wir als Minimax-Bedingung:
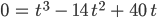
Da sehe ich gleich, dass
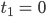
Lösung ist und dann muss ich noch
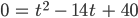
lösen. Das gibt
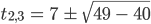
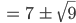
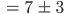
Also ist
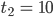
und
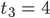
Charly Hey, Max, Du kannst ja bald Mathelehrer werden!
Max Haha! Sehr witzig! Ich werde lieber Mathebuchautor!
Charly Haha! Mit Deinen 3 Nullstellen der 1. Ableitung ergeben sich die folgenden Extremwerte:
- bei
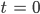 ein Minimum von ca. 11 764 m3
ein Minimum von ca. 11 764 m3 - bei
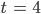 Monaten ein Maximum von ca. 11 765 m3
Monaten ein Maximum von ca. 11 765 m3 - bei
 ein Minimum von ca. 11 762 m3.
ein Minimum von ca. 11 762 m3.
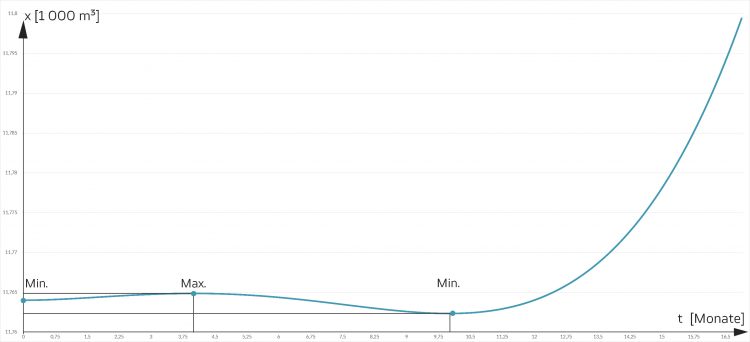
Langzeitverhalten des Gletschers
Max Aber nach 10 Monaten wächst doch die Kurve wieder an?
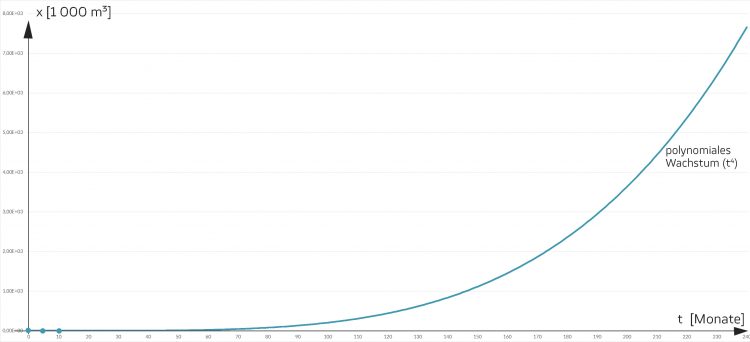
Charly Ja, mit t4! Das haben meine Schüler auch entdeckt.
Max Aber wie konnte übersehen werden, dass die Kurve für große Zeiten t polynomial wächst, dass die Minima und Maxima nur für kurze Zeit gelten? Ganz zu schweigen von der „Stabilität“ der Gletschermasse!
Charly, das ist ja der Hammer!!! Du hast die neue Eiszeit berechnet! Und was nun?
Charly Ich habe das genauso mit meinen Schülerinnen und Schülern ausgerechnet und diskutiert. Mit dieser Aufgabe wird die Ausbreitung eines Alpengletschers vorhergesagt!!! Das widerspricht allem vernünftigen Denken!!!
Max Ich verstehe Deine Wut. Es ist ein akademisches Beispiel und hat nichts mit der Realität zu tun. Hmm, sag mal, willst Du nicht mit Deiner Klasse in die Alpen fahren und das Gletschertauen beobachten, messen und besser mathematisch modellieren?
Charly Meinst Du?
Max Ich helfe Dir! Ich komme mit! Wir machen ein kleines Medienereignis daraus. Ich kümmere mich um Spendengelder und Du sprichst mit der Schulleitung und den Eltern.
Charly Und mit den Schülern!
Max Na klar!
***
Übungsaufgabe
Berechne, wann die gesamte Erde mit einem Gletscher, der in den Alpen beginnt und 30 m hoch ist, nach dieser Formel überzogen sein wird.
Lösung
Bei einer Oberfläche von 510 000 000 km2 (Wiki, 22.11.2019) erhält man 49 500 Monate = 4 125 Jahre.
