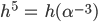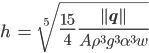Heute geht es wieder nach draußen zum Hintereisferner, diesmal nicht zum Ausblick, sondern direkt ins Eis. Charly, Max, Finja, Fabian und Justin schauen sich das Eis genauer an. Heute ist ein Spezialist von der Uni dabei, Max und Charly natürlich auch.
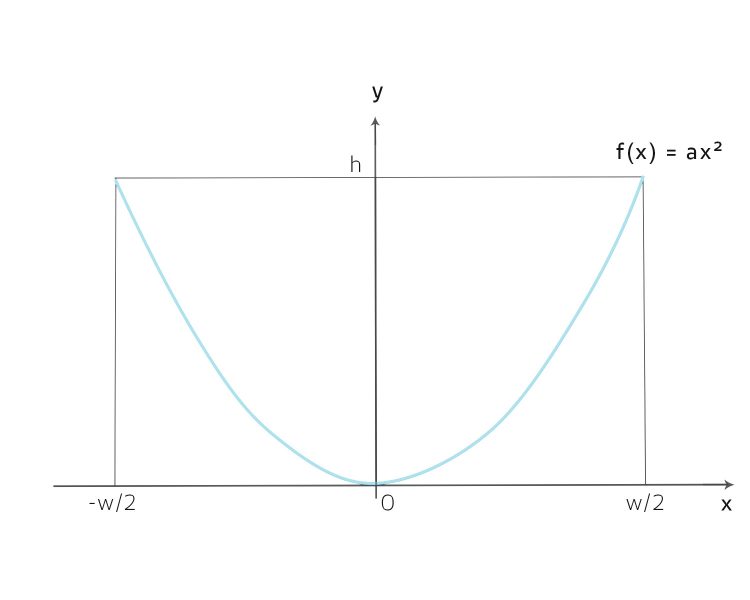
Spezialist Kinder, wir haben an der Uni ein Modell für alle Kees - ah - Gletscher der Welt gemacht. Wir können damit ausrechnen, wie sich das Eis entwickelt. Schaut mal hier, dieser Hintereisferner liegt in einem Tal, da können wir mal einen parabolischen Querschnitt annehmen.
Finja Ja gut, aber dieser Querschnitt gilt doch nicht überall!
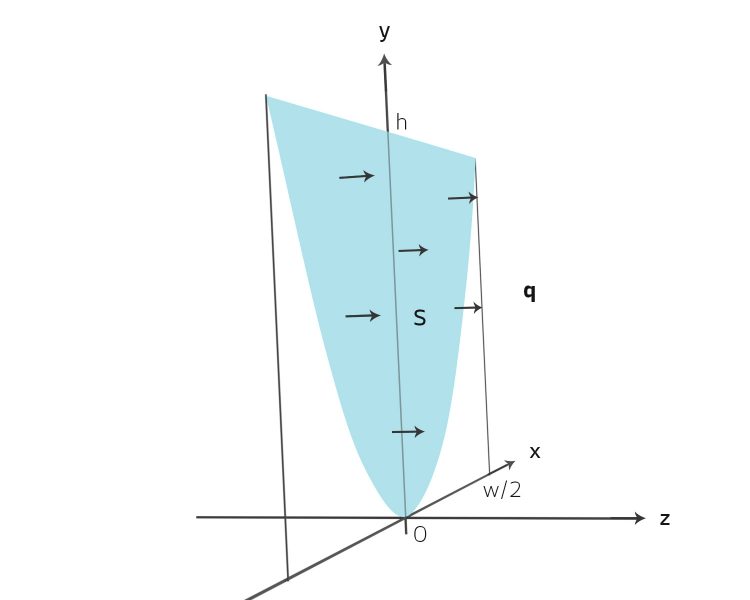
Spezialist Richtig! An der Zunge vorne wird die Fläche sehr klein – und am Gipfel ist sie größer und mittendrin, an einer Stelle im Schatten vielleicht am größten. Stellt euch eine Linie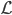 
entlang des Kees vor: Vom Gipfel bis zur Zunge. Entlang dieser Linie nehmen wir jeweils einen parabolischen Querschnitt an.
Finja O Mann, so was hatten wir noch nicht! Der Gletscher windet sich ja, dann ist die Linie 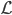ja gar keine Gerade?
Spezialist Recht so, wir haben a krummliniges Koordinatensystem.
Jetzt stellt euch mal vor, hier an dieser Stelle, wollen wir die Änderung des Querschnitts berechnen, wie das Eis schmilzt oder wächst. Wenn wir das können, dann können wir das an jeder Stelle, und dann können wir die Eisentwicklung des gesamten Hintereisferners berechnen! In den letzten Jahren gab es im Sommer mehr Verluste als im Winter dazu kam. Vor allem, weil sich auch hier in den Alpen die mittlere Temperatur erhöht hat.
Justin Verstehe! Aber wie können wir denn hier an dieser Stelle die Höhe h messen?
Spezialist Gute Frage! Wir können die Breite messen, aber nicht die Höhe. Die berechnen wir. Das will ich euch erklären! Das erste Gletschergesetz geht so:
1. Gletschergesetz
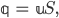
q … Fluss des Eises
S … Fläche (Surface) eines Querschnittes
u … mittlere Flussgeschwindigkeit des Eises
Justin Verstehe, aber wir haben weder S noch u.
Spezialist Aber wir können q messen, jedenfalls an einer kleinen Stelle. q ist ein Vektor, seine Richtung wird durch die Geschwindigkeit u bestimmt.
Justin Okay!
2. Gletschergesetz
Spezialist Weiter. Jetzt kommt das 2. Gletschergesetz, das glensche Fließgesetz über das Zusammenhang der mittleren Geschwindigkeit mit anderen Parametern:
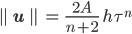
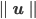ist die Länge des Vektors u:
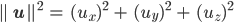
A … Kriechparameter in 1/(s Pa³)
τ … Basal shear stress
n = 3
Fabian Kriechparameter?
Spezialist Ja, richtig, Kriechparameter. Er beschreibt, wie sich das Eis unter seiner eigenen Last sich verformt.
Fabian Und – Basal Shear stress?
Spezialist Dieser Parameter beschreibt, wie das Eis unter seiner eigenen Last den Berg runter rutscht.
Fabian Aha! Rutscht das Eis jetzt auch?
Spezialist Ja, jetzt auch, vor allem, wo du da stehst!
Fabian Haha!
Justin Wissenschaft ist sehr witzig!
Spezialist Klar. Für A haben wir Werte für den Hintereisferner, ja, und für τ gibt es noch das 3. Gletschergesetz:
3. Gletschergesetz
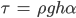
ρ ... Eisdichte in kg/m³,
g … Erdbeschleunigung in m/s²,
α ... ein Parameter für die Oberflächenform, er kann aus der Kurve 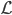bestimmt werden und wird meist geschätzt, 
.
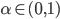Fabian Oh, Mann!
Justin Haben sie auch Werte für α?
Spezialist Ja, wir haben das simuliert, für jeden Gletscher muss man das α bestimmen. Wir haben das Hintereisferner-Alpha.
Justin Dann können wir ja alles ineinander einsetzten. Das 3. Gesetz in das 2. Gesetz:
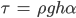
in
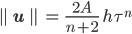
ergibt
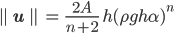
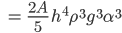
Und das noch in das 1. Gesetz:
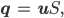
da müssen wir den Vektor u noch anders schreiben:
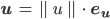
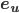ist der Vektor in dieselbe Richtung wie 
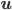und mit der Länge 1. Das ergibt
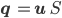
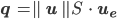
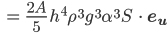
Jetzt brauchen wir nur noch S.
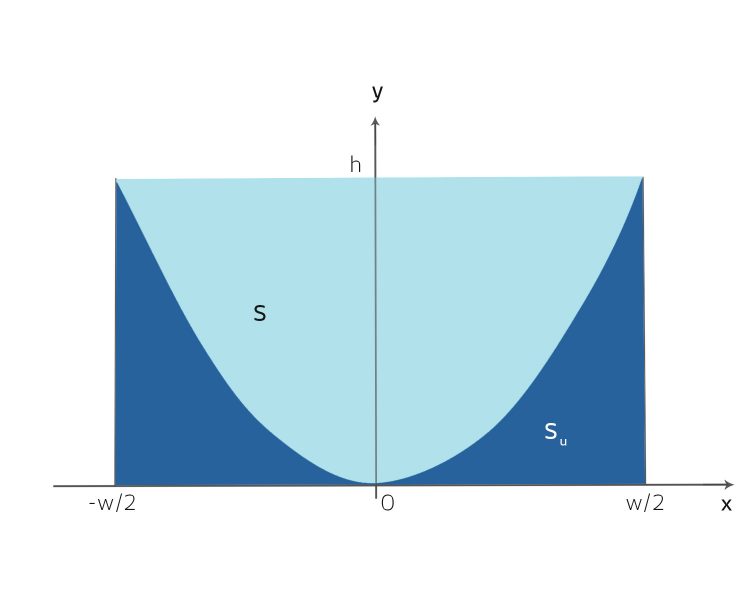
Finja Ich glaube, das kriegen wir hin: Wir haben ja die Parabelgleichung
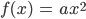
und wir wissen, dass der Punkt
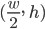
auf f liegt, wartet, …
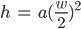
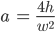
Die Fläche Su kann ich durch Integration berechnen:
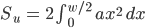
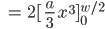
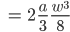
S ist dann die Rechteckfläche mit der Höhe h und der Breite w minus Su, so:
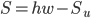
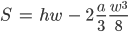
Jetzt kann ich den Wert a von der Parabel einsetzen:
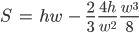
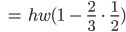
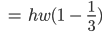
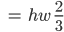
Spezialist Stimmt, Finja. Genauso Machen wir es, wir haben dann aus Justins Einsetzerei
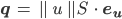
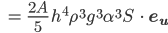
und mit deinem S für Parabelflächen:
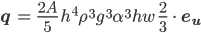
Die finale Formel für die Gletscherhöhe
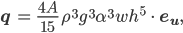
das ist die Formel zur Berechnung von h!
Fabian Was können wir tun? Haben sie denn schon alles ausgerechnet?
Spezialist Nein, wir haben das Modell erstellt und uns mit anderen Wissenschaftlern geeinigt, das für alle Gletscher der Welt zu nehmen, es heißt The Open Global Glacier Model. Ihr könnt jetzt selbst die Eisdicke damit bestimmen ...
Fabian Ja, das machen wir, ich wollte schon immer Gletscher vermessen. Komme ich dann in die Zeitung?
Max Ja, klar, gib dir mal Mühe, ich fotografiere dich!
***
Übungsaufgaben
- Wo steckt die Temperaturabhängigkeit?
- Wie hängt h von α ab?
- Wie kann man die Formel zur Berechnung von h nach h umstellen?
- Rechne ein paar Beispiele mit n = 3, ρ = 900 kg/m³ und geeignetem A.
Lösungen
- In .
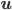- Aus
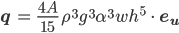
folgt
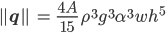
und daraus
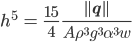
Also
