Charly, Max, Finja, Fabian und Justin sind immer noch auf Expedition am Hintereisferner. Charly ist ihr Lehrer, der Alles organisiert, Max ist sein Freund, der Alles für die Sponsoren und die Schule fotografiert. Sie haben diskutiert, dass es nicht genügt, aus den Messwerten Vorhersagen durch Interpolation zu machen, denn man kann durch geeignete 4 Punkte sowohl das Wachsen des Gletschers als auch durch andere 4 Punkte das Schmelzen des Gletschers vorhersagen. Außerdem haben sie die wichtigsten physikalischen Prozesse am Gletscher besprochen und überlegt, wie man die Gletscherhöhe aus physikalischen Messgrößen berechnen kann. Jetzt wollen sie Vorhersagen über die Gletscherentwicklung machen.
Das Open Global Glacier Model
Spezialist Unser Open Global Glacier Model benutzt für Vorhersagen die partielle DGL:
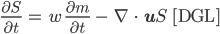
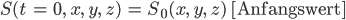
Fabian Sorry, ich verstehe gerade Bahnhof! Können sie das uns bitte mal erklären?
Spezialist Na klar! S ist die Fläche eines Querschnittes mit Parabel- oder Rechteckform. Ihr Wunderwuzi habt ja schon herausgefunden, dass
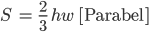
oder
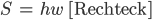
ist.
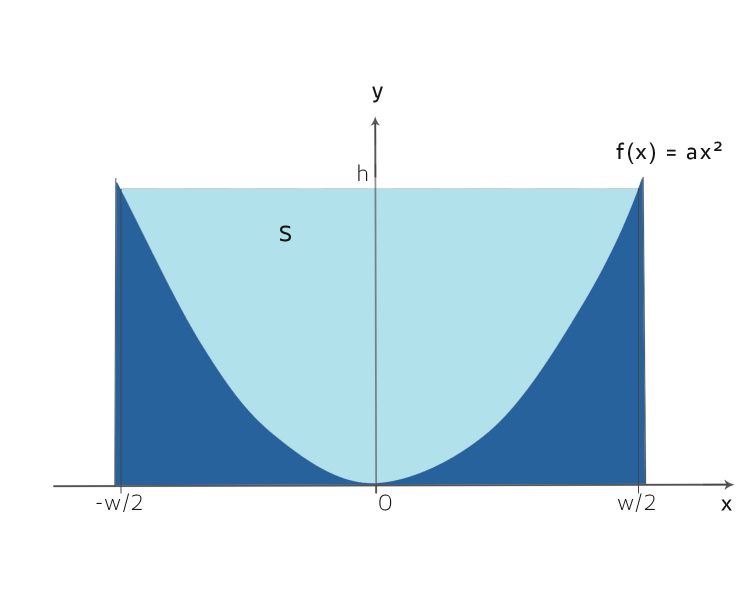
Wir können das offen lassen und schreiben
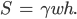
Fabian Gut, für dieses γ nehmen wir
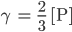
oder
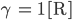
Spezialist Leiwand! Entlang eines Kees – mathematisch heißt das entlang eines Weges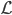 
– nehmen wir eh dieselbe Querschnittsform, wenn auch mit wechselnden Weiten und Höhen:
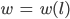
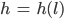
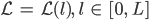entlang des GletschersFabian Gut, verstehe.
Spezialist Die partielle DGL ist ident auf der linken Seite vom Gleichheitszeichen:
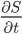
Das ist die Änderung der Fläche S mit der Zeit …
Fabian Stopp! Sehe ich das richtig, wenn sich die Fläche S ändert, dann bleibt der Gletscher doch in seinem Tal, oder? Er rutscht zusammen oder wächst? Etwa so?
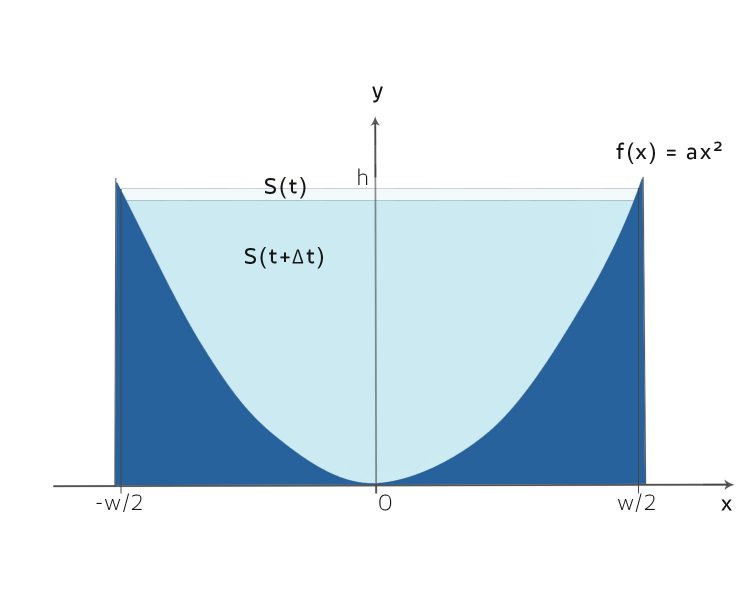
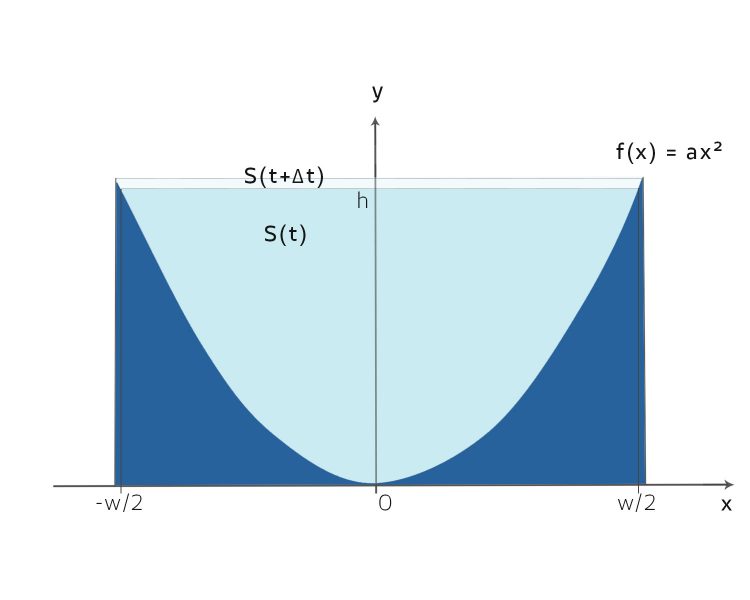
Spezialist Stimmt, Fabian, da Kees bleibt im Tal. Die rechte Seite der Gleichung bringt nun daher: a Änderung von S wird durch a Änderung der Masse mal Breite verursacht und dazu kommt noch a Änderung des Eisflusses
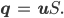
Ihr müsst euch am Vorzeichen des Flusses anhalten.
Justin Aha, eine Art Massenerhaltungssatz?
Spezialist Stimmt! Außerdem müssen wir für die Berechnung der Keesdynamik den Querschnitt zu einer Referenzzeit vollständig kennen oder annehmen, für jeden Punkt auf dem Weg 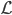, das schreibt man dann so:
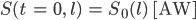
Vereinfachung des OGGM
Justin Okay, verstehe. Sieht ja alles linear aus! Sie haben doch gesagt, wir haben die Beziehung
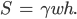
Zwischen S, h und w. Die können wir doch mal einsetzen in
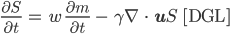
Dann kriegen wir mit der Produktformel für die Ableitung:
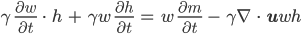
Jetzt teilen wir durch γw, ist ja immer positiv, das geht dann
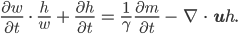
In der letzten Woche haben wir ja Alles vermessen und berechnet, bei uns war das Verhältnis von Höhe zu Weite sehr klein
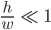
außerdem war blieb die Eismasse unserer Proben zeitlich und räumlich fast konstant. Da können wir doch die Änderung auch mal als konstant ansetzen:
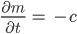
Und die Eisströmung änderte sich ebenfalls kaum, wisst ihr was, wir setzen
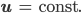
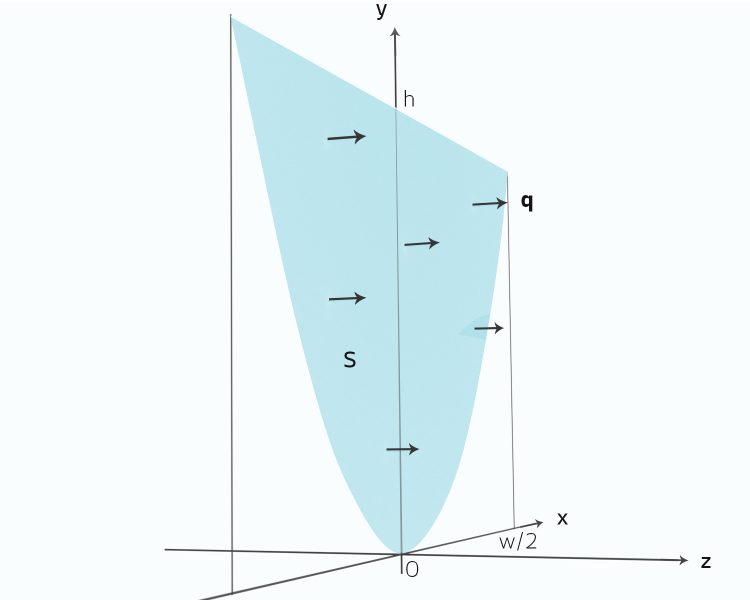
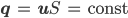
Spezialist Oja! Ihr seid aber fesch!
Justin Wir können ihre Gleichung dann lösen! Es ist dann nämlich
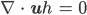
und es bleibt nur noch
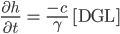
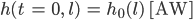
übrig!
Spezialist Recht so!
Lösung des vereinfachten Modells
Finja Na klar! Wir haben bei Charly schon DGLs gelöst! Das ist ja gar nicht so schwer! Wir brauchen nur zu integrieren:
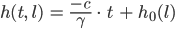
Spezialist Sowas macht ihr bei euch in Bonn? Alle Achtung! Super!
Finja Danke! Wenn ich mal ein h0(l) nehme, das am Gipfel 1340 m über der Zunge liegt und nach
l = 6,8 km
zu 0 wird, in 50 Jahren hat sich die Frontposition um .....?
Spezialist Von 1960 bis 2010 hat sich die Zunge von -1 703 m auf -2 666 m gegenüber 1770 zurückgezogen.
Finja Ah, danke, dann...
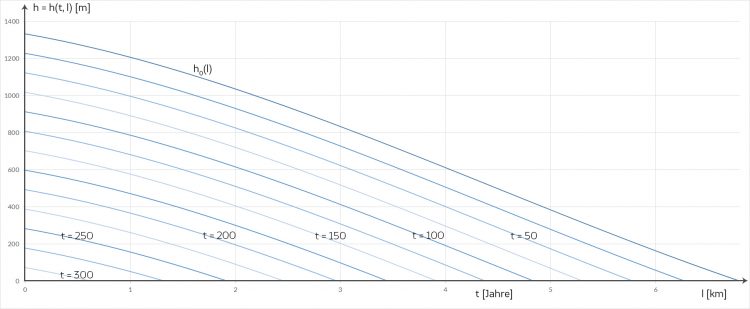
... dann wird diese Höhenlinie h0 gleichmäßig kleiner und nach 300 Jahren ist fast nichts mehr übrig vom Hintereisferner!
Spezialist Finja, ihr habt zwar toll gerechnet, eure Vereinfachungen spiegeln die Situation wieder, an die die ganze Region lange Zeit geglaubt hat: ein langsames Keesschmelzen , so langsam wie bisher. Doch das ist nicht richtig. Man muss Alles urgieren. Wir haben ein viel schnelleres Keesschmelzen berechnet als du.
Fortsetzung folgt.
***
Übungsaufgabe
Finde einen geeignten Anfangswert h0(l) und löse die vereinfachte DGL damit.