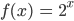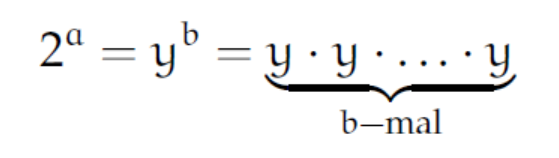Fabian, der praktisch Veranlagte, kämpft sich allein zu Hause durch seine Aufgaben. Er soll die Exponentialfunktion und ihre Ableitung verstehen. In seinem Buch wird die Funktion
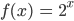
untersucht. Er findet die Wertetabelle ...
Exponentialfunktion für ganzzahlige x
| x | 2x |
| -3 | 0,125 |
| -2 | 0,25 |
| -1 | 0, 5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
... ganz richtig. Alles klar. Er zeichnet die Funktionswerte in ein Diagramm.
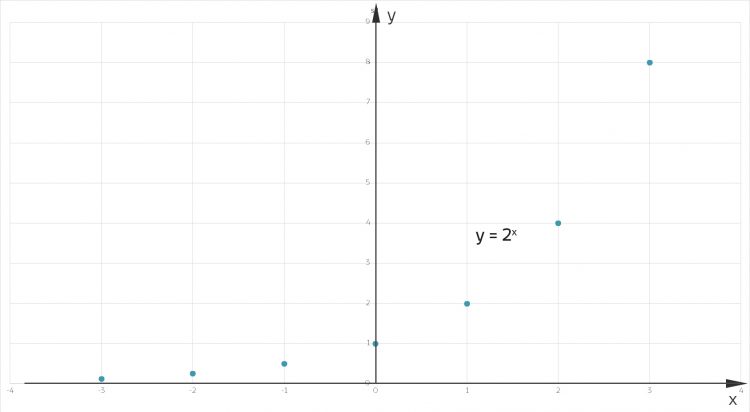
Doch das reicht nicht, er soll die Zeichnung zur Funktion mit dem grafikfähigen Taschenrechner (GTR) erstellen und eigentlich eine durchgehende Linie zeichnen, so:
Doch sein GTR funktioniert seit der Reise nicht mehr, weder grafisch noch sonst wie. Er fragt sich, ob man die Werte für die Funktion außer denen aus der Tabelle auch ohne so einen GTR ausrechnen kann. Er ist mal wieder sehr wütend, weil ihm da was aufdoktriniert wird, was nicht nachvollziehbar ist.
Er weiß nicht weiter und ruft Justin an.
Exponentialfunktion für rationale x
Fabian Hi Justin, wie geht’s? Ich habe ein Problem mit dieser 2x-Kurve. Mein GTR tut’s nicht!
Justin Hi Fabian! Was, dein GTR tut’s nicht? Dann bist du ja echt aufgeschmissen! Aber im Buch ist doch die Kurve gezeichnet.
Fabian Ja, hab‘ ich gesehen. Ich will die Kurve aber selbst ausrechnen! Ich verstehe, was 2-3, 2-2, 2-1 usw. ist, aber was ist mit den Werten dazwischen? Zum Beispiel, wenn
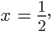
was ist dann
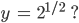
Justin Es ist nicht schwer! Zuerst nimmst du das Potenzgesetz:
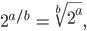
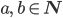 .
.
Fabian Was meinst du?
Justin 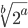 ist die b-te Wurzel aus 2a: Es ist
ist die b-te Wurzel aus 2a: Es ist
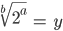
genau dann, wenn
Fabian Und wie rechne ich das aus?
Intervallschachtelung für √2
Justin Lass uns dein Beispiel nehmen:
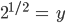
Das ist bedeutet:
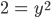
Welche Zahl zum Quadrat ergibt 2?
Fabian y muss zwischen 1 und 2 liegen.
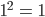
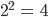

Justin Richtig! Jetzt teilst du das Intervall und berechnest für y = 1,5 das Quadrat.
Fabian Okay,
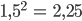
Das ist größer als 2! Also muss y zwischen 1 und 1,5 liegen.

Justin Jetzt halbierst du das Intervall [1; 1,5]. Das nennt sich Intervallschachtelung.

Fabian Krass! Das kann ich mit dem Handy machen, warte mal, ich rufe dich gleich wieder an!
***
Fabian Hallo Justin, ich habe
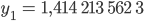
herausbekommen und
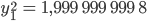
Außerdem ist
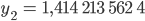
und
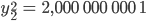
Weiter geht’s nicht!
Justin Hey Fabian, das ist doch toll, du hast jetzt die Wurzel aus 2 gezogen und eine Genauigkeit von 10-9 erreicht. Der GTR hat nur eine Stelle mehr.
Fabian Aber es ist nicht korrekt.
Justin Stimmt! Die Wurzel aus 2 ist irrational, du kannst immer nur eine Näherung berechnen. So viele Stellen wie du brauchst, so viele berechnest du.
Weitere Werte für rationale x ∈ [0, 1]
Fabian Okay, das wird jetzt philosophisch! Und wie rechne ich die vielen anderen Werte für x zwischen 0 und 1 aus?
Justin Lass uns mal 10 Stellen dazwischen nehmen: 0,1; 0,2; …
Diese Zahlen sind gut als Brüche zu schreiben:
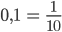
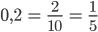

Jetzt nimmst du wieder das Potenzgesetz.
Fabian Okay, ich versuch‘s:

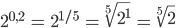

Jetzt muss ich das nur noch mit dieser Intervallschachtelung machen. Okay, ich versuch‘s!
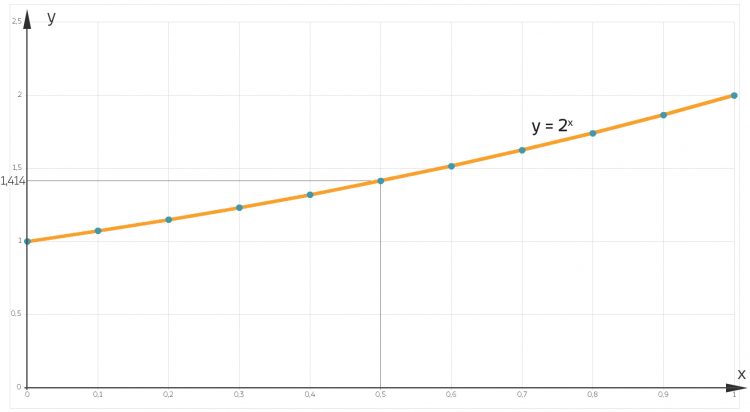
Dustin Hey Fabian, super, dann kannst du ja bald bei Texas Instruments anfangen!
***
Übungsaufgabe
Berechne selbst Näherungswerte für