Fabian, der praktisch Veranlagte, kämpft sich immer noch allein zu Hause durch seine Aufgaben durch. Er hat nun die Exponentialfunktion
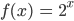
verstanden. Jetzt geht es um die Ableitung der Funktion. Dazu sollen die Schüler und Schülerinnen ihren GTR benutzen und damit die Ableitung dieser Funktion berechnen, um dann die Formel für die „richtige“ Ableitung f‘(x) zu erraten. Die Ableitung und die originale Funktion haben einen Quotienten von
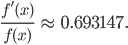
Numerische Berechnung der Ableitung der Exponentialfunktion
Das versteht er nicht. Es beschäftigt ihn, er versteht die Zahl nicht. Außerdem findet Fabian das ganze Vorgehen etwas merkwürdig. Zu allem Unglück funktioniert sein Taschenrechner nicht. Wie soll er ohne eine Formel die Ableitung berechnen? Der GTR muss ja auch eine Formel nehmen, aber welche? Er studiert die beiden Graphen im Lehrbuch und hat keinen Schimmer, wie er das verstehen soll.

Da ruft er Justin an.
Justin Hi, Fabian, wie geht’s?
Fabian Hi, Justin! Ich hab‘ schon wieder ein Problem. Wir sollen mit dem GTR die Ableitung von
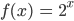
berechnen. Geht das auch ohne GTR?
Justin Fabian, warte mal, ich schaue mal, ob die Formel für die Ableitung im Handbuch steht … ja, hier! Die ist online! Hier:

Fabian Okay! Wieso nehmen die nicht

für den Differenzenquotienten?
Justin Das ist auch ein Differenzenquotient, er heißt zentraler Differenzenquotient. Er mittelt den rechten und den linken Funktionswert neben dem Wert an der Stelle x geteilt durch ihren Abstand 2h. Geometrisch ist es der Anstieg der Strecke durch diese beiden Nachbarn zu f(x). Außerdem steht hier, dass
h = 0.001
standardmäßig eingestellt ist.

Fabian Okay, verstehe! Danke! Dann berechne ich mal die Näherung für f‘(x) an ein paar Stellen und zeichne eine Kurve dazu.
***
Verhältnis von f(x) und f'(x) – Numerische Berechnung
Seine Zeichnung sieht wie die im Buch aus. Er freut sich. Das ist toll.
Weil sich die beiden Kurven so ähnlich sind, legt das Buch nahe, dass sich die beiden Funktionen f(x) und f‘(x) nur durch eine Konstante unterscheiden. Auch das berechnet er an einigen Stellen und findet mit h = 0.001 dieselben Werte wie im Buch:

Das Verhältnis der beiden Kurven ist ungefähr
0.6931
Aber was bedeutet diese Zahl? Schließlich ist sie aus einer Näherung entstanden. Selbst wenn die Mathematiker keine Formel für die richtige Ableitung finden, hat er
0.6931
als Quotient ausgerechnet. Er ruft Justin noch einmal an.
Fabian Justin, ich bin‘s noch mal!
Justin Hi, Fabian!
Fabian Ich habe jetzt den Quotienten von f‘ und f an ein paar Stellen ausgerechnet und kriege ungefähr
0.6931
heraus. Wie kommt das?
– Analytische Berechnung
Justin Schau mal, wir sollen das Verhältnis von f‘(x) und f(x) für
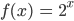
bestimmen. Da nehmen wir beide mal den üblichen Vorwärtsdifferenzenquotienten für f‘ und rechnen das Verhältnis aus:

Fabian Okay. Und weiter? Das Potenzgesetz?
Justin Ja, das Potenzgesetz:


Fabian Okay! Dann ist der Quotient gar nicht mehr von der Stelle x abhängig! Warum haben sie im Buch nicht diese 2 Zeilen hingeschrieben und uns stattdessen 8 Näherungswerte mit immer demselben h ausrechnen lassen? Die Aufgabe ist ja eigentlich, den Grenzwert für

auszurechnen!
Justin Stimmt! Mach dir nichts draus. Es kommt, wie's kommt. Wenn du jetzt ganz scharf auf die Formel schaust, siehst du



Fabian Hey! Krass! Der Quotient ist der Anstieg an der Stelle Null! Ohne Näherung! Ich habe das nur näherungsweise ausgerechnet.
Justin Ja. Fabian, du kennst doch die Ableitung der e-Funktion?
Fabian Klar, das ist wieder die e-Funktion. War ja immerzu in den Medien. Das weiß jetzt jedes Kind!
Justin Mit einem kleinen Trick können wir unsere Funktion mit der e-Funktion schreiben:

Versuch doch mal, davon die Ableitung auszurechnen!
Fabian Klar, ich versuch’s:

das ist die e-Funktion mal "innere Ableitung" der e-Funktion, eben ln 2. Warte, jetzt muss ich das nur noch an der Stelle x = 0 ausrechnen:


Super! Ich habe zwar keinen funktionierenden GTR, aber ich schätze mal, dass

ist? Stimmt's? Und es ist

Justin Ja, super!
***
Übungsaufgaben
Berechne die Ableitung von

und

Wie ist das Verhältnis von f'(x) zu f(x)?
Lösungen