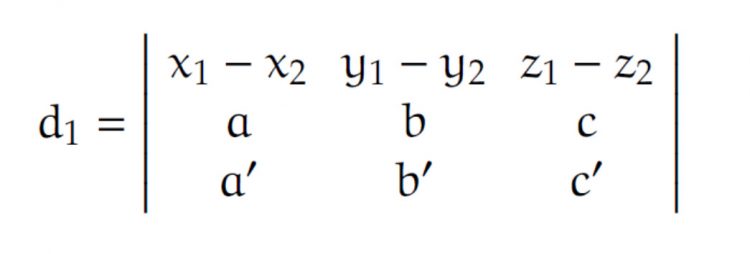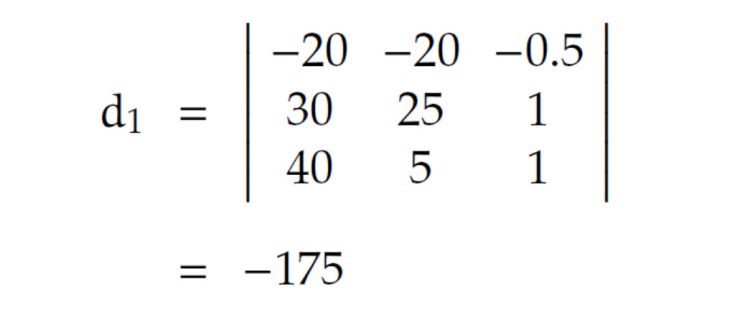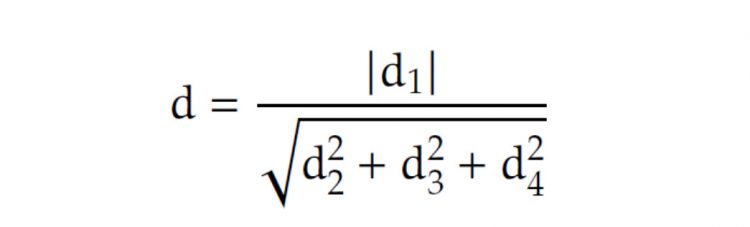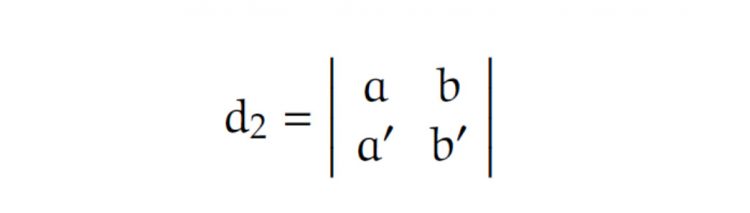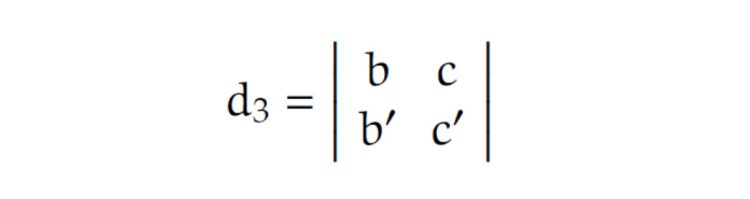Charly ist nun mal in Berlin und heute schafft er es endlich, Rike zu treffen. Sie freuen sich. Rike fragt Charly, wie es ihm geht. Hat er auch schon Abi-Aufgaben betreut? Kennt er die Berliner Aufgaben? Der Tagespiegel hat sie wegen des großen Protestes veröffentlicht. Hier ist die Aufgabe über einen Tunnelbau. Gegeben sind die Punkte N(Nord), S(Süd), A und B im R³. Zwischen N und S soll ein (geradliniger) Autotunnel gebaut werden, zwischen A und B ein (geradliniger) Bahntunnel. In der Mitte zwischen N und S soll ein Lüftungsschacht gebaut werden, der beim Punkt L mitten zwischen N und S auf der Straße beginnt. Eine weitere Notzufahrt in den Autotunnel vom Punkt P aus ist vorgesehen. Beide Tunnel sind Unterführungen eines Berges. Zum Lüftungsschacht gibt es noch die Information über die Tangente an den Berg an der Stelle, wo er aus dem Berg herausragt. Charly und Rike schauen sich typische Tunnel an und sehen, dass die Tunneleinfahrt recht eben und die Einfahrten als Verlängerung des Tunnels gebaut werden.
Abiaufgaben-Setting
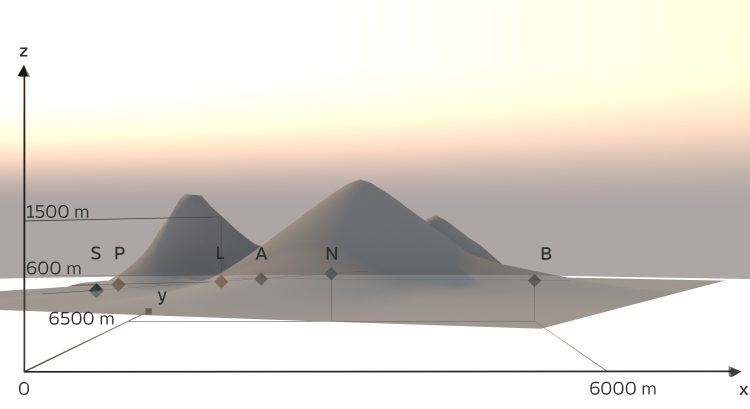
Rike ist skeptisch. Sie entwirft die Situation 3D.
Charly Okay, alle beide Tunnel in der Höhe 600 – 700 m? Wie der Simplon-Tunnel! Hey, der Simplon-Tunnel war wohl ein echtes Vorbild! Aber Dein Bild, Rike, ist viel zu unübersichtlich!
Koordinatensystem und Karte
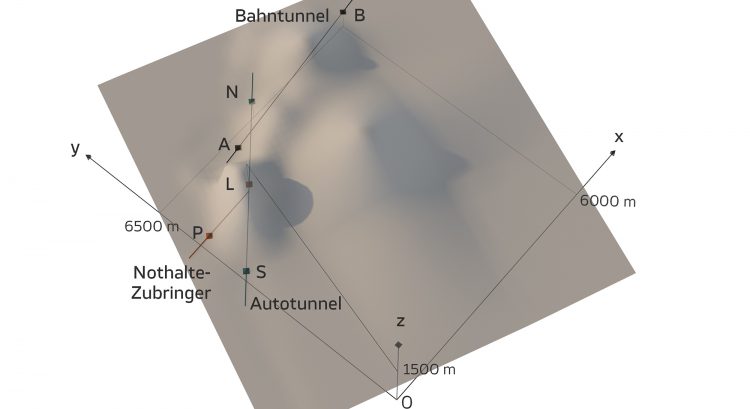
Rike Okay, ich kann das drehen. Ich drehe das so, dass der Punkt S im Süden liegt und der Punkt N im Norden, ja? Außerdem habe ich den Zubringer gleich mit eingezeichnet. Der beginnt bei P und soll eine weitere Zufahrt zum Tunnel für Notfallsituationen sein. Der hat natürlich auch eine flache, gerade Zufahrt, ja, Charly?
Charly O, nein, ich fasse es nicht! Das Koordinatensystem ist jetzt schräg im Raum! Es ist nicht wie eine geografische Karte! Wie soll man sich da zurechtfinden! Eigentlich liegt S im Westen und N im Osten! Hast Du noch eine andere Ansicht?
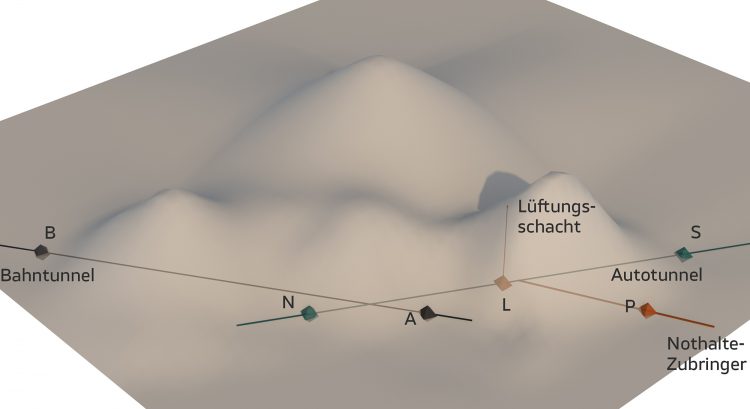
Rike Klar, hier, eine perspektivische.
Charly Ja, die ist gut, jetzt versteh' ich die Situation. Sollen wir mal die Aufgabe lösen, ob die beiden Tunnel sich treffen?
Rike Klar, ich sehe es hier 3-dimensional und kann sogar den Abstand der Tunnel messen. Warte mal hier, ja, die Tunnel haben von ihrer Mitte den minimalen Abstand von ca. 30 m zueinander.
Charly Das ist ja gerade das Ziel der Aufgabe. Wenn sie sich nicht treffen, dann können die beiden Tunnel gebaut werden, das ist der Tenor. Aber ehrlich, soll man den jungen Leuten suggerieren, dass zwei Tunnel gebaut werden, wenn sie sich nicht berühren? Das finde ich nicht gut!
Sag mal Rike, wie hast Du denn die Berge gezeichnet?
Rike Na so, dass sie die Tunnel bedecken. Und das die Bedingung mit der Tangentialebene am Lüftungsschacht erfüllt ist.
Charly Könntest Du nicht vorn noch einen schönen alpinen Berg zeichnen?
Rike Klar, das könnte ich. Aber dann kommt keiner mehr von N, A und P weg. Dann wären die Tunnel eine Sackgasse!
Charlys Alternative
Charly Haha! Du sag mal, wenn ich mir das so ansehe, wo das alles recht flach auf der einen Seite des Berges ist, dann könnte man ja dort eine Straße und Bahntrasse legen, wäre das nicht viel besser?
Rike Ja, warte mal, hier, stimmt!
Charly Oh, Mann! So ein Shit!
Übungsaufgaben
- Überprüfe, ob sich die beiden Tunnel AB und SN berühren für
- Wenn nicht, welchen Abstand haben die beiden Geraden?
- Wie ist der Fehler gegenüber Rikes Zeichnung einzuschätzen?
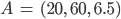
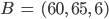
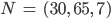
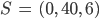
und 1 LE = 100 m.
Lösungen
- Der 1. Tunnel in Parameterschreibweise (Auto)
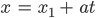
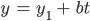
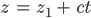
mit
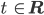 und im Beispiel mit
und im Beispiel mit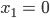
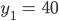
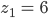

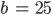
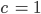
Der 2. Tunnel in Parameterschreibweise (Bahn)
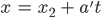
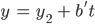
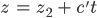
mit
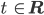 und
und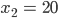
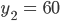
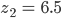
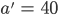
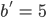
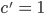
Beide Geraden schneiden sich genau dann, wenn
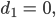
wobei
[Formel aus Bronstein]. Bei uns ist
also sind die beiden Geraden der Tunnel windschief zueinander.
- Abstände der Tunnel
Dafür gibt es eine ebenda Formel für den minimalen Abstand d der beiden Geraden:mit
Wir erhalten mit den obigen Werten
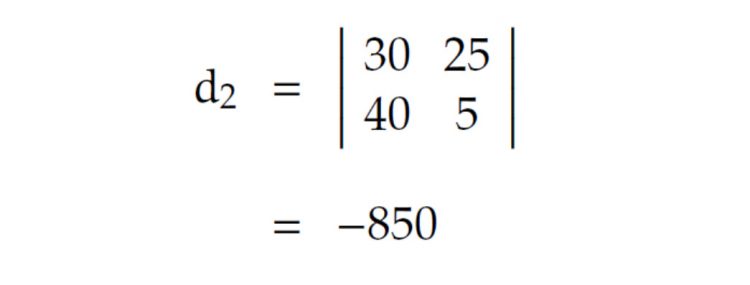
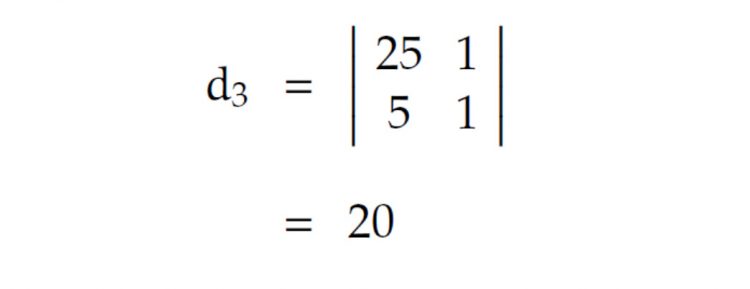
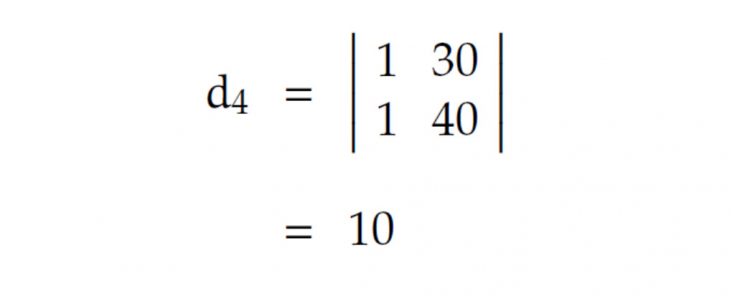 und schließlich für den Abstand d:
und schließlich für den Abstand d: Die Tunnel wurden in der Aufgabe als Geraden ohne Dicke angenommen. Da erscheint der Abstand von 21 Meter der Mitten der Tunnel als sehr gering und es ist sehr fragwürdig, ihn zu bauen.
Die Tunnel wurden in der Aufgabe als Geraden ohne Dicke angenommen. Da erscheint der Abstand von 21 Meter der Mitten der Tunnel als sehr gering und es ist sehr fragwürdig, ihn zu bauen. - Rike hatte 30 m in ihrer grafischen Lösung gemessen. 9 m/21 m = 42 % erscheint sehr viel. Die Zeichnung wurde allerdings angelegt mit einer längsten Seite von 6 500 m, das ergibt einen Fehler von: 9 m / 6 500 m = 0,13 %.