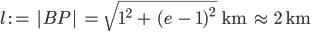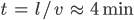Charly, Lila und Max sitzen abends zusammen. Charly berichtet über die neusten Katastrophen aus dem Matheunterricht, so zum Beispiel von einer Autobahnaufgabe für die 11. Klasse. Die Aufgabe geht so:
Die Autobahnaufgabe
Gegeben ist die Funktion
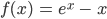
Sie beschreibt den Verlauf einer Autobahn. (1 LE = 1km)
a) Besitzt f Extrem- und Wendepunkte?
b) Schließen Sie aus den Ergebnissen, dass f keine Nullstellen besitzt.
c) Vom Bahnhof B(0|0) führt ein Zubringer zum Punkt P (1|f(1)) der Autobahn. Zeigen Sie, dass dieser Zubringer tangential in die Autobahn mündet.
d) Wie lange benötigt ein 30 km/h schneller Transporter vom Bahnhof zur Autobahn?
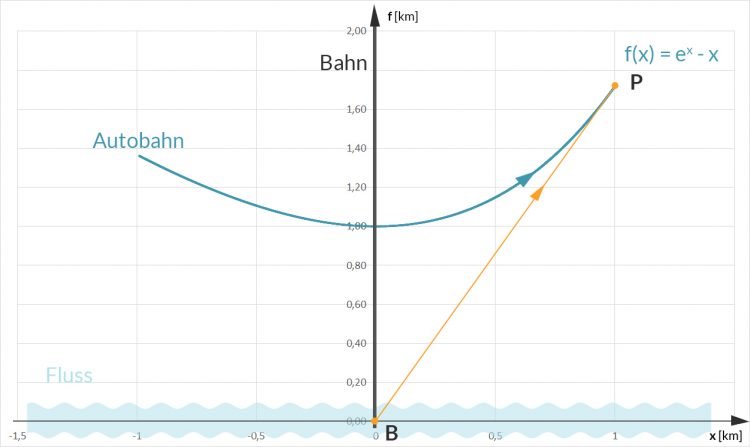
Die verkehrstechnische Situation
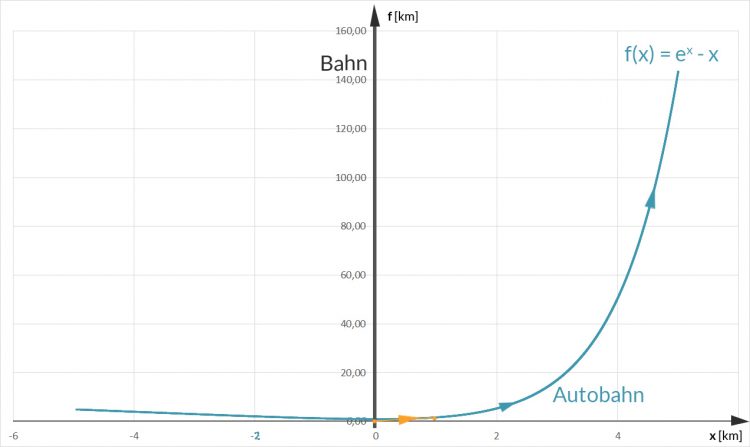
Charly Ist ja eine typische Kurvendiskussion mit Berechnung der 1. und 2. Ableitung und einer Tangenten. So weit so gut, doch was soll die ganze Anwendung mit der Bahnlinie, Autobahn und dem Fluss? Hat mich doch tatsächlich ein Schüler darauf angesprochen, wie sinnvoll es ist, an der Kreuzung von Fluss und Bahn einen Container-Umladeplatz und einen Autobahn-Zubringer zu bauen, um dann die Waren auf die Autobahn statt auf die Bahn zu bringen. Er meinte, wenn man in etwas größerem Maßstab schaut und den Warentransport entweder vom Norden mit der Bahn bis zum Nullpunkt, vom Süden mit der Bahn oder von Osten oder Westen mit dem Schiff und dann weiter die Autobahn entlang verfolgt, so:
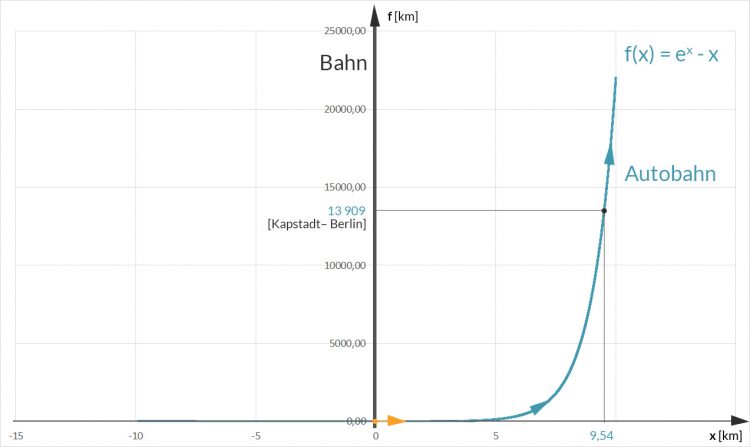
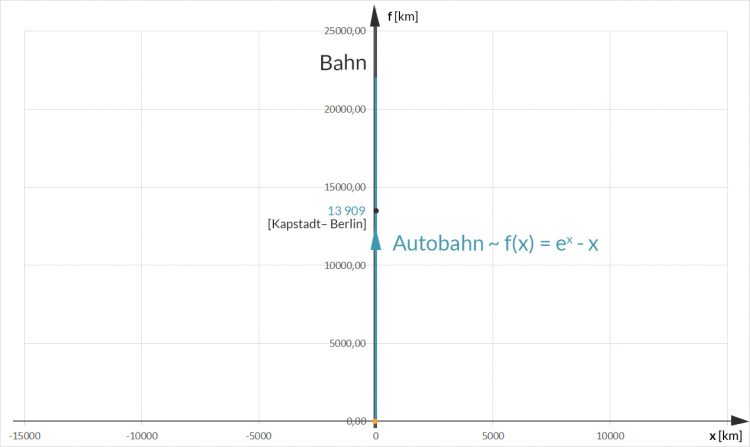
dann verliert die Autobahn neben der Bahn jeden (Realitäts-)Sinn. Schaut man von weiter oben auf die Verkehrssituation, so kriegt man wegen des exponentiellen Wachstums von f sehr große Entfernungen:
Kapstadt – Berlin
Wenn man nur 9,54 km nach rechts von der Bahn kommen will, muss man 13 909 km nach Norden zurücklegen, das entspricht etwa der Länge der Strecke Kapstadt-Berlin!
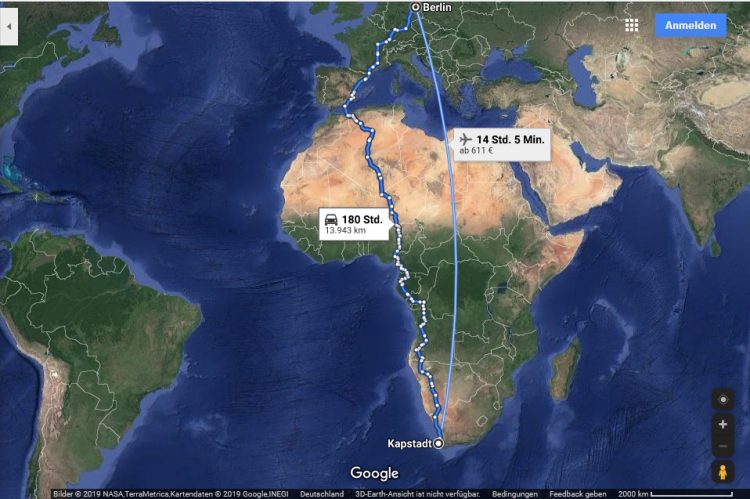
Und wenn man diese maximale Skalierung der x-Achse aufgibt und beide Achsen gleichmäßig skaliert, verliert die Verkehrslösung mit dem Zubringer und Umladen der Container ganz ihren Sinn.
Max Was hast Du darauf geantwortet?
Charly Der Schüler hat sich nicht für meine Antwort interessiert. Er musste dann ganz schnell weg, Fridays for Future!
Max und Lila Hahaha, da bist Du ja noch einmal davongekommen!
***
Übungsaufgaben
Löse die Aufgaben a)-d)
Lösungen
a)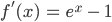 
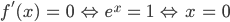
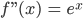
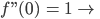Min.
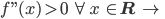keine Wendepunkte
b) Weil das Min. bei (0, 1) liegt und es keine weiteren Extrema gibt, gibt es keine kleineren Werte als 1 und somit keine Nullstellen.
c) Zubringer: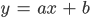 
(0, 0) liegt auf der Geraden, also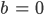 
(1, e - 1) liegt auf der Geraden, also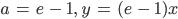 
Tangente von f an P mit dem Anstieg: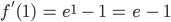 
Anstieg der Geraden: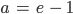 
Beide Anstiege sind gleich.
d) 
