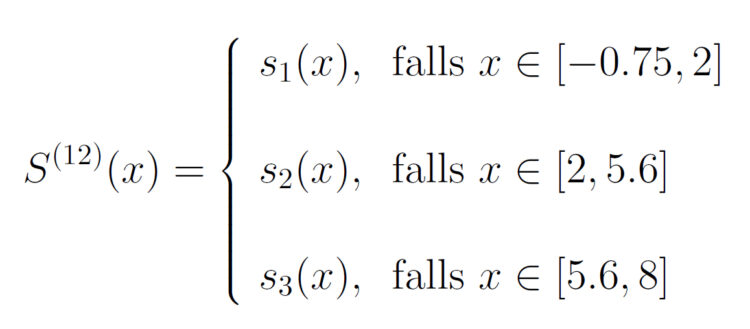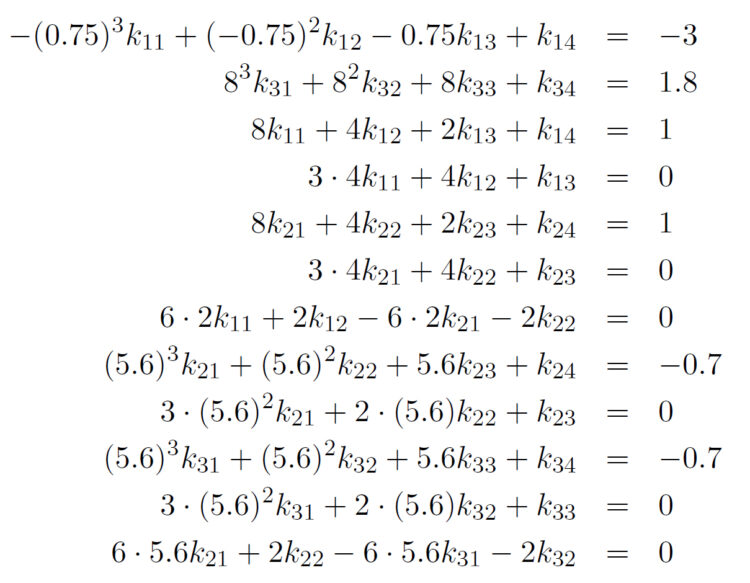Als Charly vom Joggen wiederkommt, findet er Rike ganz verzweifelt. Sie hat sich die schräge Ellipsenaufgabe noch einmal vorgenommen und Charlys Funktion 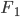
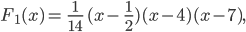
genauer angeschaut. Sie bemerkt, dass diese Funktion  nur für einige
nur für einige  sehr gut mit der Vorlage übereinstimmt, aber leider nicht an anderen wichtigen Punkten.
sehr gut mit der Vorlage übereinstimmt, aber leider nicht an anderen wichtigen Punkten.
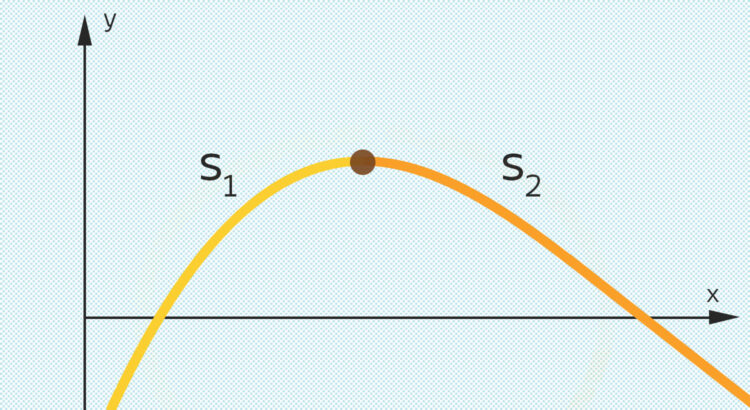
Rikes Kritik an Charlys Polynom
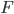 . Abbildung nach [Ott, Schomburg, 2021]
. Abbildung nach [Ott, Schomburg, 2021]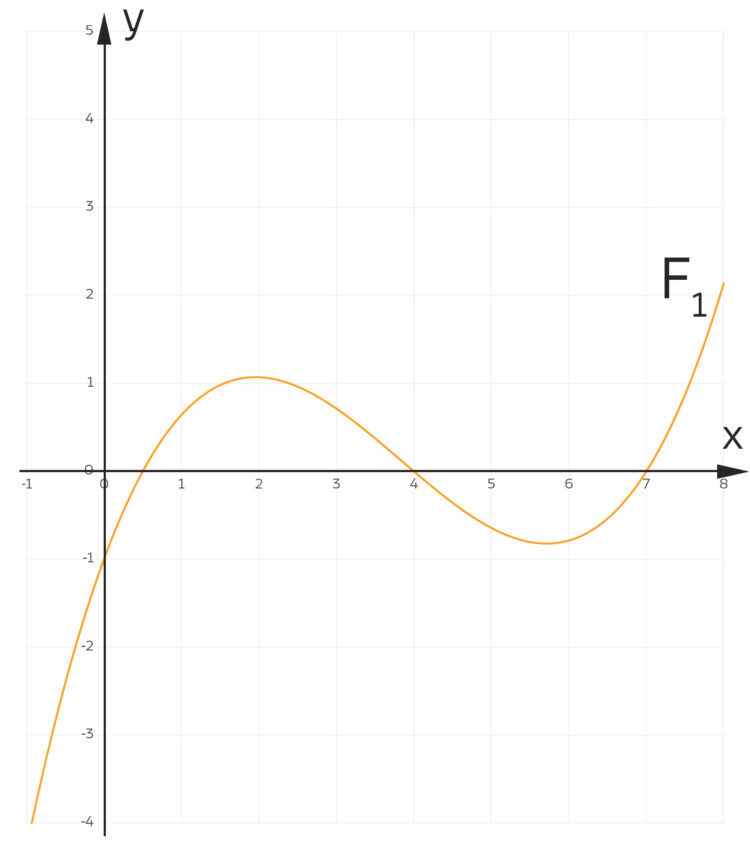
 mittels Polynom-Ansatz
mittels Polynom-AnsatzCharly Rike, sag mal, bist du immer noch bei der schrägen Ellipse?
Rike Ja, Charly, dein Ansatz funktioniert an den Nullstellen und beim Absolutglied wunderbar. Hier schau mal, ich habe einige Abweichungen gefunden, vor allem bei  :
:
 | 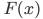 | 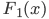 | 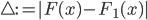 | 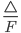 |
| -0.67 | ca. -2.7 | -3 | 0.3 | ca. 11 % |
| ca. -0.75 | -3 | -3.279 | 0.279 | 9 % |
| 2 | 1 | 1.071 | 0.071 | 7 % |
| 6 | ca. -0.6 | -0.785 | 0.185 | 30 % |
| 8 | ca. 1.8 | 2.1 | 0.3 | 17 % |
Abweichungen der beiden Kurven an einigen Stellen
Charly Naja, ein Fehler von 10 % ist doch noch akzeptabel. 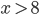 kommt in den Teilaufgaben nicht vor und für das verschwindende Integral integrieren wir höchstens bis
kommt in den Teilaufgaben nicht vor und für das verschwindende Integral integrieren wir höchstens bis 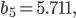 das haben wir selbst ausgerechnet. Rike, mach dir keine Sorge, vermutlich war es nur eine Nachlässigkeit beim Zeichnen.
das haben wir selbst ausgerechnet. Rike, mach dir keine Sorge, vermutlich war es nur eine Nachlässigkeit beim Zeichnen.
Rike Eine Nachlässigkeit bei einer Abiaufgabe? Das entschuldigst du? 10 % Abweichung sind für dich okay? Hast du nicht gesagt, beim Lernen geht um verschiedene Methoden, die Schüler und Schülerinnen dürfen auch mal in eine Sackgasse rennen? Doch wenn es um deinen Ansatz geht, ist alles ok?
Charly Willst du sagen, dass ich ein Nachlässigkeitslehrer bin?
Rike Nein, du bist ein Dickkopf!
Charly schaut sehr finster.
Rike War nicht so gemeint. Lass uns mal versuchen, dieses 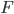 besser zu bestimmen. Charly, du hast die Nullstellen und das Absolutglied als Referenz genommen. Und jetzt stimmen die Funktionswerte am Rand und in der Nähe der Extrema nicht.
besser zu bestimmen. Charly, du hast die Nullstellen und das Absolutglied als Referenz genommen. Und jetzt stimmen die Funktionswerte am Rand und in der Nähe der Extrema nicht.
Charly Aber bei den Nullstellen passt mein Polynom sehr gut.
Rike Sehr witzig, das sind genau 3 Punkte!
Charly Na gut, dann war das wohl eine Sackgasse! Laufen wir jetzt in die nächste?
Rike Ich weiß noch nicht, ob es eine Sackgasse wird, ich bin noch dabei, die ganze Sache ist etwas aufwendig, ich habe mich schon drei Mal verrechnet…
Charly Das glaube ich nicht!
Rike Doch, du kannst es glauben.
Charly Was ist dein Ansatz?
Rike Hör zu. Neben den Nullstellen sind doch noch die Extrema besondere Punkte einer Funktion. Ich werde statt der Nullstellen diese als Referenzpunkte wählen, na, und außerdem die beiden Punkte am Rand des Definitionsbereiches.
Charly Okay.
Rike Mein neuer Ansatz ist aber nicht einfach ein Polynomansatz für das ganze Intervall, sondern etwas ganz anderes, ein Spline-Ansatz.
Charly Ein Spline-Ansatz?
Rike Ja, ein Spline-Ansatz.
Charly Was ist das?
Spline-Ansatz mit 3 Stücken
Rike Wir zerlegen die gesuchte Funktion in geeignete Teilstücke, ich habe mit 3 Teilstücken angefangen: vom linken Rand bis zum Maximum, von da bis zum Minimum und von da bis zum rechten Rand.
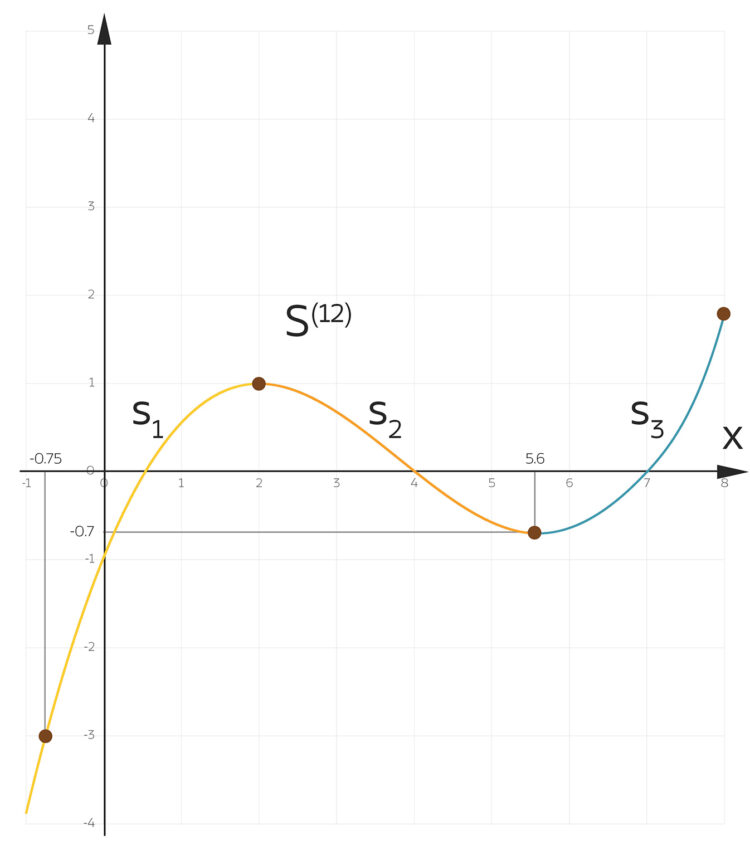
Für jedes Teilstück setzen wir ein kubisches Polynom 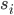 an:
an:
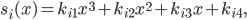
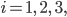 das sind die kubischen Polynome.
das sind die kubischen Polynome.
Charly Okay, das sind die Polynome. 3 Polynome mit je 4 unbekannten Koeffizienten, das ergibt 12 Unbekannte!
Rike Ja, 12 Unbekannte. Für die entwickeln wir sinnvolle Bedingungen. An den Rändern haben wir die Funktionswerte:
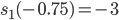
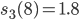
Charly Okay.
Rike An den Extremstellen fordern wir, dass die jeweiligen Funktionswerte, Ableitungen und die Krümmung übereinstimmen.
Charly Okay, dann passen die Polynome so gut zusammen, dass man das Gestückel nicht sieht?
Rike Ja, genau. Außerdem suchen wir ja eine differenzierbare Funktion.
Charly Genau. Eine Stammfunktion. Aber ausrechnen möchte ich die Koeffizienten nicht…
Rike Ist alles halb so wild, also wir haben an der Stelle 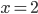
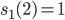
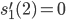
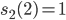
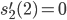
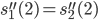
An der Stelle 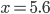 geht es ebenso, ich glaube das kannst du auch.
geht es ebenso, ich glaube das kannst du auch.
Charly Okay, ich versuche es. Wie groß ist der Funktionswert an dieser Stelle?
Rike Na, vielleicht -0.7?
Charly Okay, wir versuchen das:
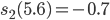
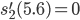
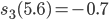
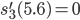
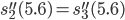
Rike Stimmt!
Charly Jetzt haben wir die 12 Bedingungen für die 12 Unbekannten. Das müssen wir nur noch in die Polynome einsetzen.
Lösung und Kritik
Rike Ja, das habe ich schon gemacht, hier ist das Gleichungssystem für die Koeffizienten  :
:
Charly Und wie lösen wir das? Das war doch die hilfsmittelfreie Abiaufgabe?
Rike Wenn du Lust hast, kannst du das mit dem Gaußverfahren lösen, das funktioniert mit den 4 Grundrechenarten. Ich habe ein tolles Tool gefunden: matrixcalc.org. Das rechnet mir die Lösungen innerhalb von Sekunden aus, hier:
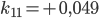
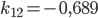
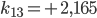

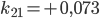
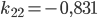
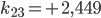

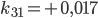
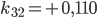
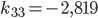
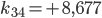
Charly Super!
Rike Thanks! Dabei hatte ich mich mehrfach verrechnet. In der Grafik sieht man dann, ob die 3 Stücke zusammen passen.
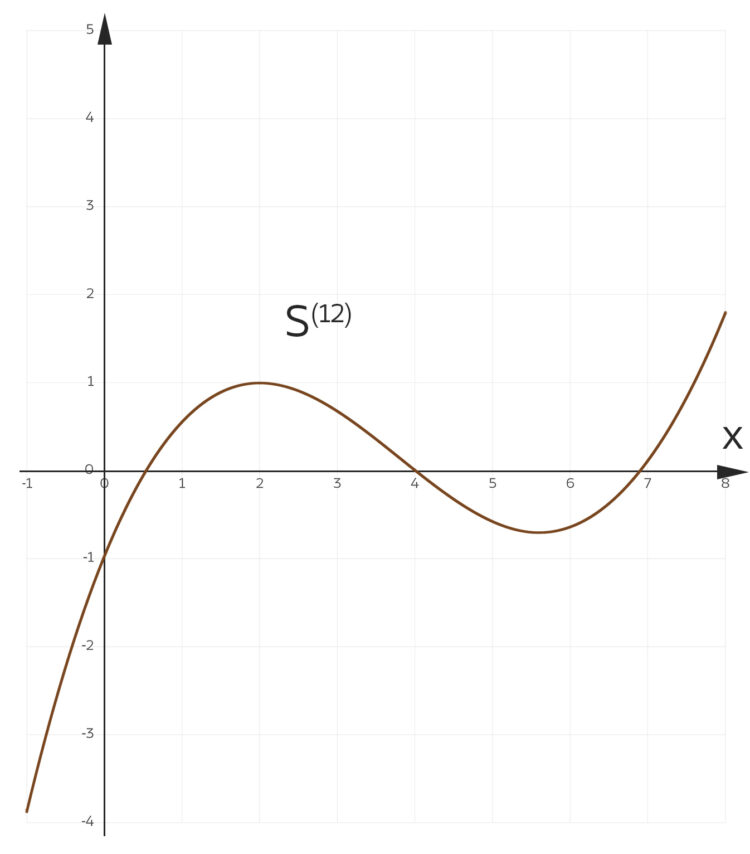
Charly Jetzt hat das Zusammensetzen gut geklappt, ich bin gespannt, ob dein Spline  besser als mein Polynom
besser als mein Polynom  ist.
ist.
Rike Naja, das Zusammensetzen hat jetzt endlich geklappt. Bis zur ersten Extremstelle sieht das Spline ganz passabel aus, doch an der Stelle 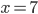 haben wir keine Nullstelle. Ich habe da einen Funktionswert von
haben wir keine Nullstelle. Ich habe da einen Funktionswert von
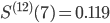
Charly Bloß gut, dass ich den relativen Fehler nicht ausrechnen kann, Division durch Null!!! Eine Stelle nach dem Komma ist falsch, das ist ziemlich ungenau. Wie kommen wir aus dieser Sackgasse wieder raus?
* * *
Übungsaufgaben
- Wie groß ist schätzungsweise der Arbeitsaufwand zum Lösen der linearen Gleichungssysteme ohne technische Hilfsmittel?
- Wie könnte das Problem des großen Fehlers für
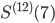 gelöst werden?
gelöst werden?
Lösungen
- Rike hat für das Aufstellen und Lösen ca. 8 h gebraucht.
- siehe nächster Beitrag