Charly und Rike feiern heute ihre neue Wohnung. Ein paar Freunde sind gekommen, so auch Ida. Ida macht gerade ihr Refendariat in Informatik an einem Gymnasium. Sie hat ein kleines Problem zur Berechnung von Zufallszahlen mitgebracht, das sie mit Rike besprechen möchte.
Rike Ida, na, wie geht es dir an deiner Schule?
Ida So weit so gut. In Informatik habe ich eine tolle 10. Klasse, wir haben Python zusammen kennengelernt. Das hat Spaß gemacht!
Rike Das hört sich gut an.
Ida Bei meiner Vorbereitung bin ich aber auf ein Problem gestoßen, das ich alleine nicht lösen kann. Vielleicht kannst Du mir helfen?
Rike Ich versuch’s! Erzähl‘ doch mal!
Zufallszahlen in Python
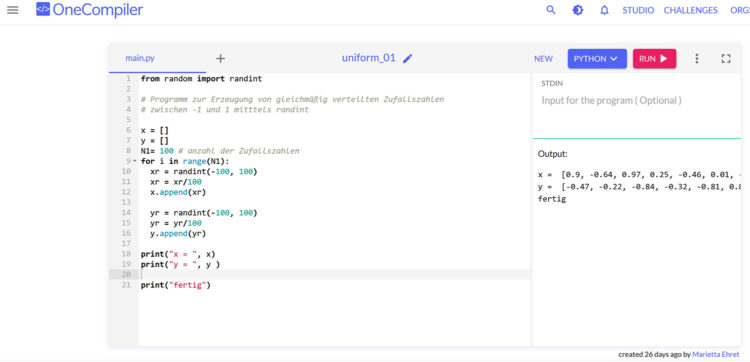
Ida Ich möchte gerne Zufallszahlen erzeugen. Sagen wir mal 100 Zahlen zwischen -1 und 1. Dazu habe ich die Funktion
randint()
benutzt. Die erzeugt zufällige ganze Zahlen. Ich habe das Intervall [-100, 100] angegeben, die erhaltenen ganzen Zahlen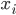 
durch 100 geteilt und in eine Liste 
geschrieben.
Rike Okay.
Ida Das habe ich gleich noch ein zweites Mal gemacht, diese Zahlen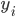 
habe ich ebenfalls in eine Liste geschrieben: 
.
Rike Okay.
Ida Dann habe ich die Punkte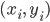 
in Excel als Diagramm dargestellt.
Rike Zeig mal her!
Ida Hier!
Gleichverteilte Zufallszahlen
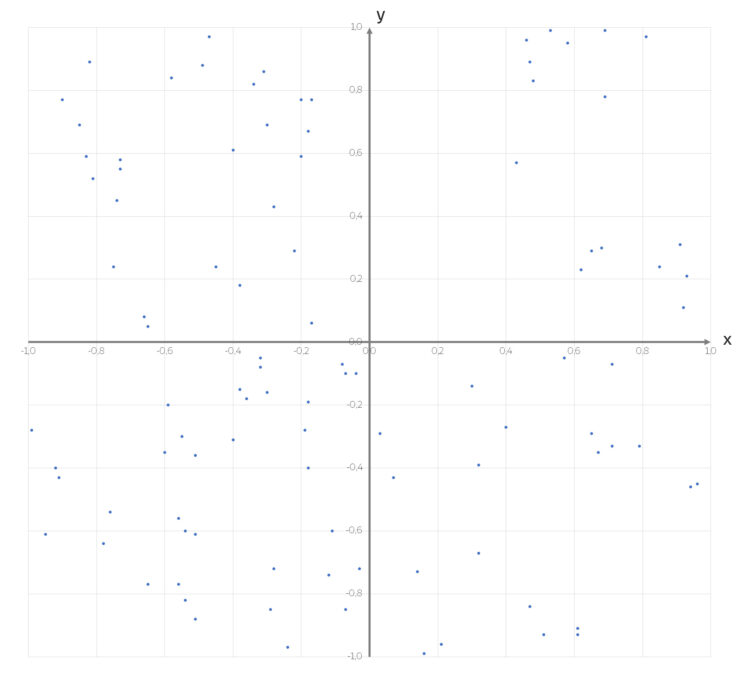
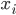und 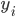als Punkte 
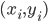in der Ebene.
Rike Das sieht gut aus.
Ida Danke! Außerdem wollte ich noch feststellen, ob die Zahlen 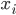und 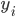gleichmäßig zwischen -1 und 1 verteilt sind. Dazu habe ich das Intervall [-1, 1] in 100 Teile geteilt und diese mit 
durchnummeriert. Dann habe ich die Häufigkeiten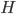 
berechnet: Wieviel Zahlen 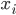bzw. 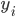liegen in den Teilen von 0 bis :
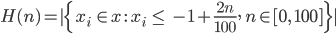
Rike Aha, so eine Art Verteilungsfunktion – nur mit 100 multipliziert?
Ida Ja, eben die Häufigkeiten.
Rike Und was hast Du herausbekommen? Wie war der Zufall?
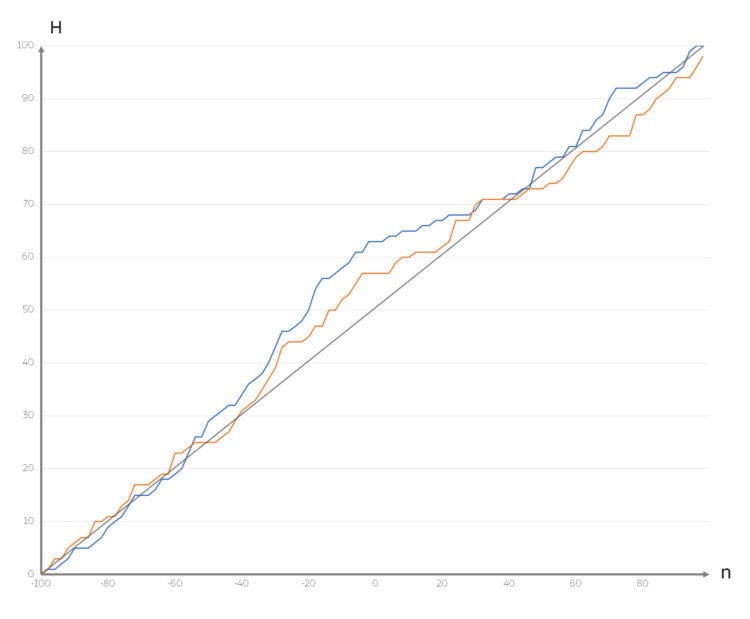
-Werte (Blau), der -Werte (orange) und der Gleichverteilung (grau)
Ida Der Zufall war sehr gut gleichmäßig verteilt. Die Häufigkeiten der -Werte sind zwar recht ähnlich zu denen der -Werte, aber das zweidimensionale Muster wirkt recht zufällig. Es ist okay so.
Rike Ja, finde ich auch. Hast du den Mittelwert und die mittlere quadratische Abweichung deiner Werte kontrolliert?
Ida Klar, der Mittelwert der 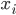-Werte liegt bei -0.08 und bei -0.03 für die 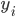-Werte. Die mittlere quadratische Abweichung liegt bei 3 %.
Rike Ist doch toll! Und was ist Dein Problem?
Nomalverteilte Zufallszahlen in Python
Ida Ich möchte gerne mal zufällige Zahlen erzeugen, die normalverteilt sind. Da gibt es doch so viele Anwendungen, das muss doch irgendwie zu schaffen sein! Also, ich hätte gern 100 Zufallszahlen mit dem Mittelwert Null und irgendeiner Standardabweichung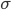 
.
Rike Okay, das verstehe ich, die Normalverteilung ist wirklich wichtig. Aber ich habe das auch noch nicht programmiert. Erzähle weiter, was hast du unternommen?
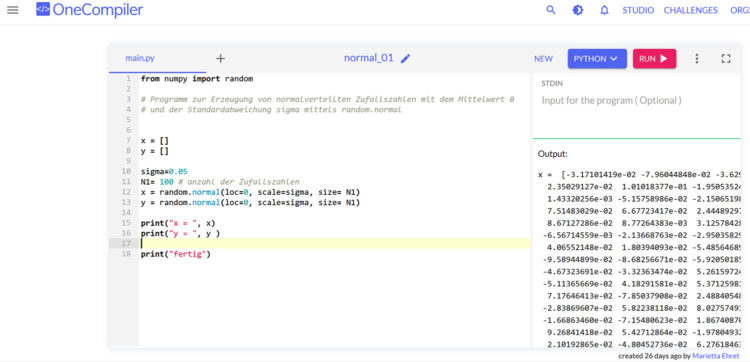
Ida Ich habe mich ein bisschen informiert… und bin auf eine Funktion
random.normal()
in Python gestoßen. Damit kann man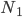 
Zufallszahlen mit einem gegebenen Mittelwert 
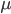und einer Standardabweichung 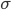erzeugen. Die habe ich benutzt:
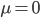
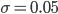
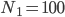
Und zwar gleich zweimal: für und . Dann habe ich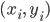 
wieder als Punkte dargestellt.
Mittelwert und Standardabweichung als wichtigste Kriterien
Die Mittelwerte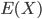 
bzw. 
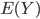für die Zufallszahlen 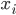bzw. 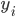habe ich überprüft. Natürlich auch die Standardabweichungen 
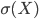bzw. 
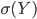. Für diese Zufallszahlen, die du hier siehst, habe ich die folgenden Ergebnisse erhalten:
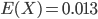
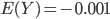
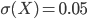
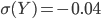
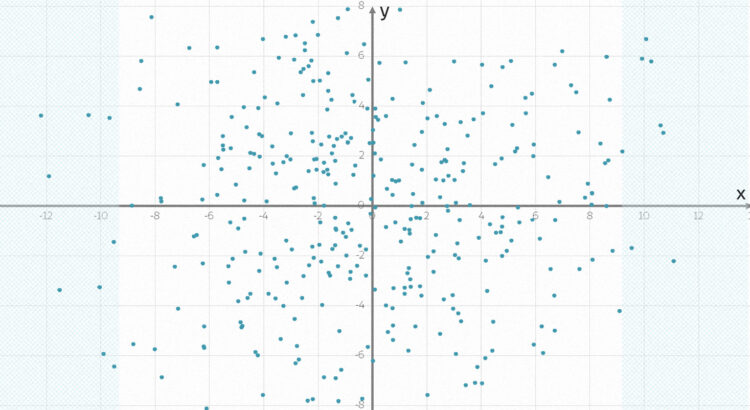
Das passt ganz gut zu den Eingabewerten meiner Funktion. Aber schau dir mal das Bild an!
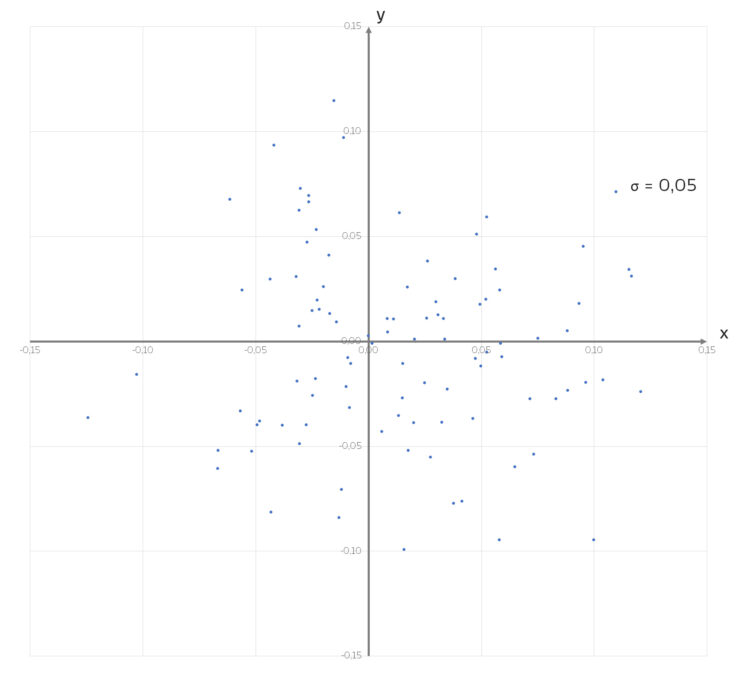
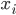und 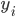mittels random.normal().
Rike Hmm, Mittelwerte und Standardabweichungen passen gut, fast zu gut. Doch so ganz überzeugend ist das nicht. Alle Zufallszahlen 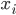und 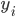sind betragsmäßig kleiner als 0.15?
Ida Ja!
Merkwürdigkeiten der Zufallszahlen
Rike Kann das mit dem 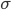zusammenhängen? Kannst du das 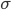ändern?
.
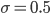Ida Klar, hier bei
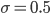
sind alle 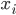- und 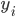-Werte betragsmäßig kleiner als 1.5. Hey, Rike,
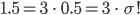
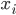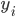Rike Was? Alle und sind betragsmäßig kleiner als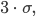 
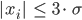
und
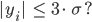
Ida Ja, für 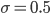auf jeden Fall.
Rike Das ist merkwürdig! Lass uns doch mal 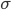in dein Diagramm einzeichnen.
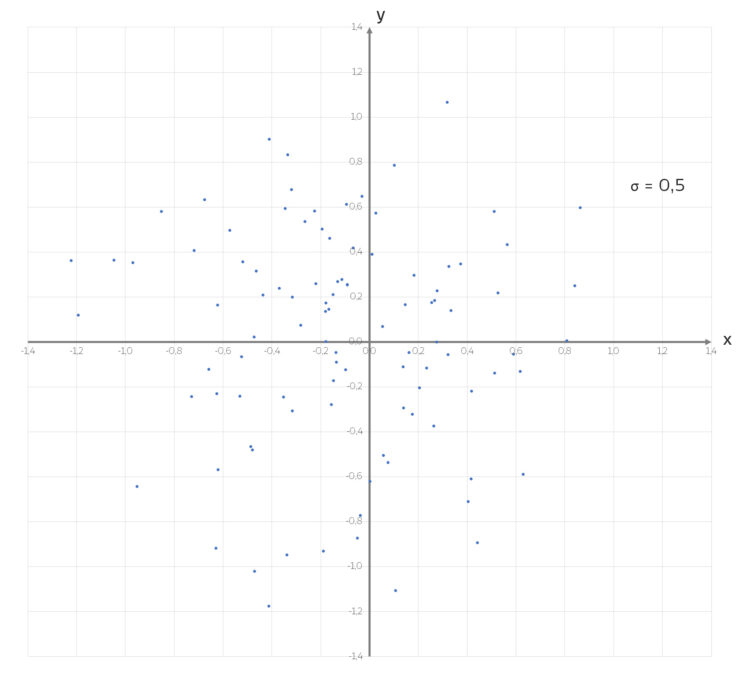
Ida Warte, …, jetzt habe ich’s!
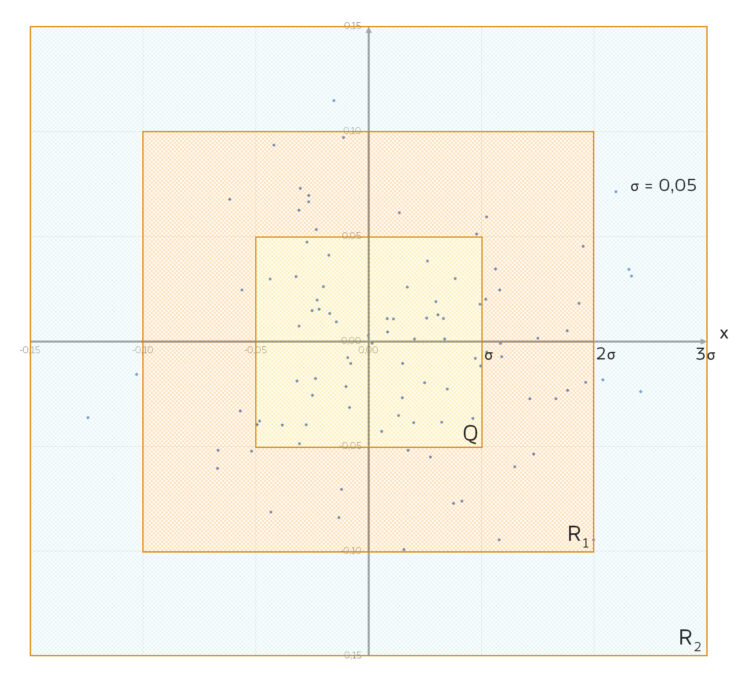
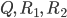in Abhängigkeit von $\sigma$. Hier mit .
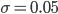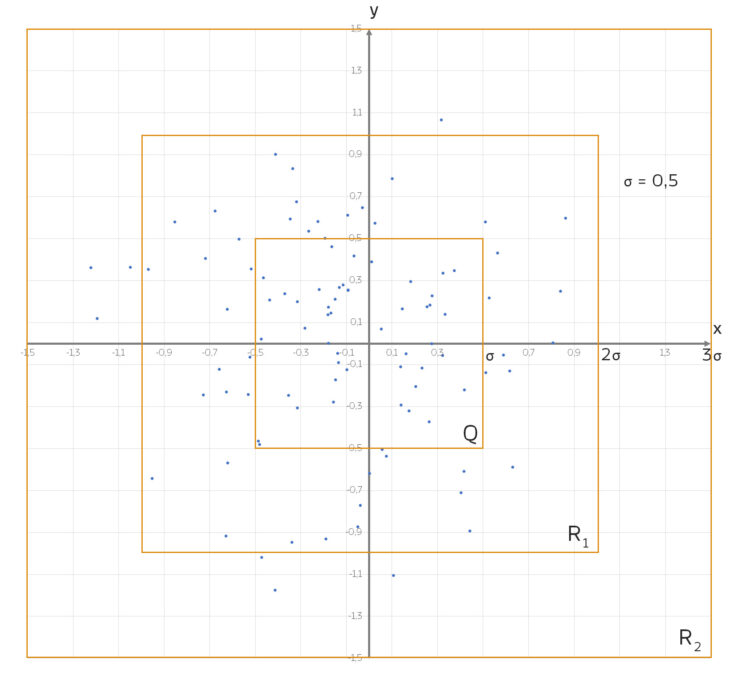
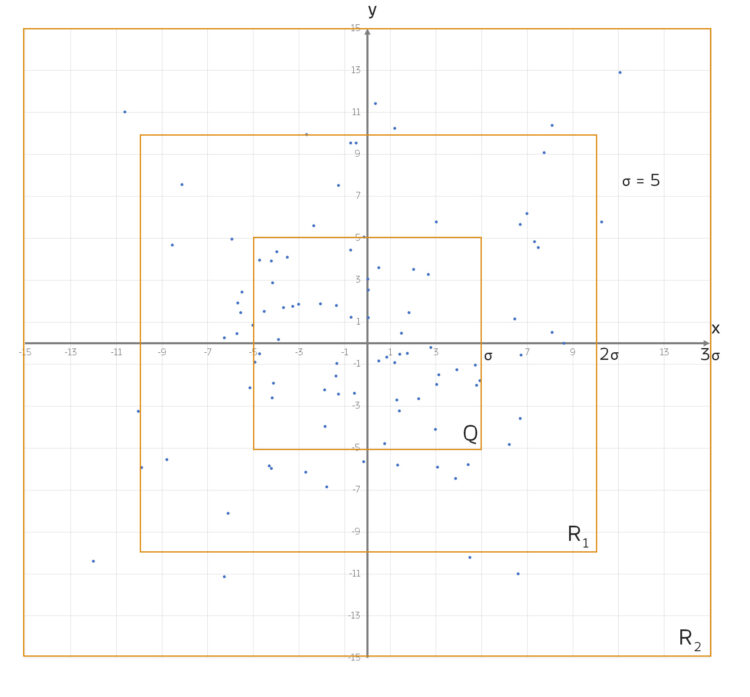
Geometrische Muster
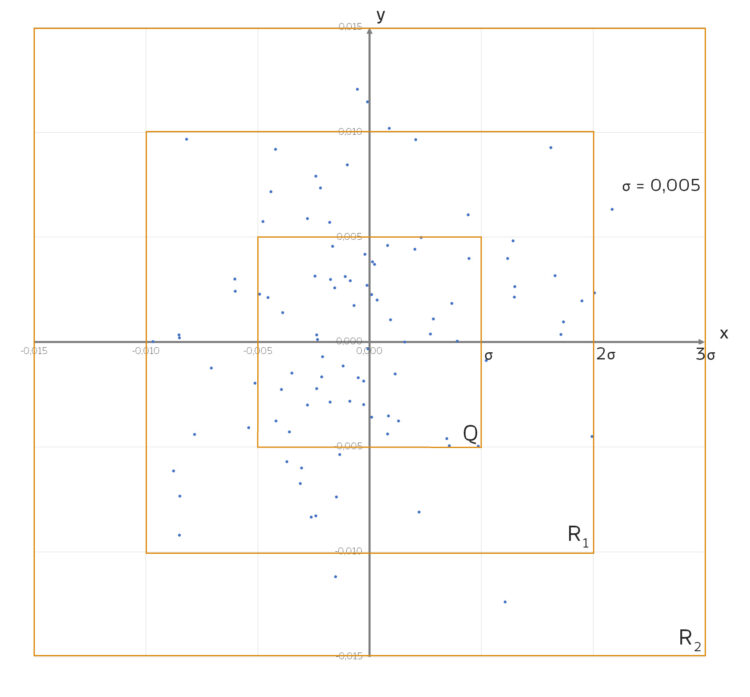
Jetzt sehen wir es deutlich, es gibt 3 Bereiche:
- das Quadrat
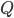um den Nullpunkt mit der Seitenlänge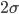 
- den Rahmen
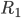mit der Dicke 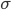um dieses Quadrat 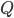herum - den zweiten, äußeren Rahmen R2 ebenfalls mit der Dicke
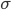
Rike Im Quadrat 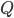wirkt die Verteilung sehr gleichmäßig.
Ida Ja, das sehe ich auch! In den beiden Rahmen aber auch, wenn auch nicht so dicht!
Rike Kannst du die Häufigkeiten der Punkte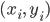 
in den 3 Bereichen zählen?
Ida Klar, kann ich, ich muss das nur programmieren, hier sind die Bilder der Punkte 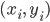für verschiedene :
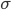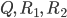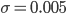
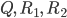für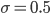 
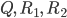für
für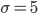 
Hier sind die Werte…. Warte, ich kann auch gleich noch die Mittelwerte ermitteln. Da die Flächen verschieden groß sind, wäre die relative Dichte doch aufschlussreich. Lass uns ein "Einheitsquadrat"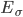 
nehmen: das Quadrat mit der Seitenlänge 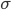und dafür die Dichte in den 3 Bereichen berechnen!
Rike Ida, das ist cool, mach doch mal!
Ida Warte...
|  |  |  | | |
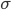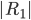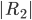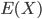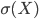| 0.005 | 51 | 42 | 7 | -0.0004 | 0.005 |
| 0.05 | 49 | 43 | 8 | 0.01 | 0.05 |
| 0.5 | 49 | 44 | 7 | -0.1 | 0.44 |
| 5 | 49 | 39 | 12 | -0.29 | 4.9 |
| Mittelwert | 49.5 | 42 | 8.5 | - | - |
| Mittelwert pro 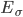| 12.4 | 3.5 | 0.4 | - | - |
Rikes Vermutung über den Algorithmus
Rike Hey Ida, das sieht nach einem klaren Algorithmus für "normalverteilte" Zufallszahlen aus, die aus der Gleichverteilung "zurecht gerückt" werden. Im inneren Quadrat 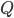liegen immer ca. 50 % der Punkte. Im Rahmen 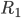liegen ca. 40 % der Punkte und im Rest liegen ca. 10 %. Deine Idee mit dem Einheitsquadrat ist super. 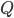hat 4 Einheitsquadrate, dann ist die Anzahl der Punkte pro Einheitsquadrat 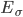ca. 12, im 1. Rahmen mit 12 Einheitsquadraten sind nur noch ca. 3.5 Punkte pro Einheitsquadrat und im 2. Rahmen haben wir weniger als einen halben Punkt pro Einheitsquadrat! Das ist der Algorithmus! So einfach ist es, man zeichnet diese Quadrate um den Mittelwert herum und verteilt auf jedes Einheitsquadrat die entsprechende Anzahl von Punkten. Fertig! Nur leider würde ich das nicht eine Normalverteilung nennen!
Ida Ja, stimmt, Rike. Diese Zufallszahlen haben zwar sehr gute Mittelwerte und Standardabweichungen, sie sind leicht zu programmieren, aber sie sind wirklich brauchbar. Das verstehen meine Zehntklässler bestimmt! Die Punkte müssten sich in der Mitte häufen und langsam nach außen hin weniger werden. Und eigentlich ist bei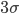 
nicht unbedingt Schluss, oder?
Rike Haha, gute Frage! Wollen wir mal überlegen, wie so ein zweidimensionales Muster aussehen sollte?
Ida Ja klar, aber jetzt feiern wir erst eure neue Wohnung!
***
Übungsaufgaben
- Teste selbst die Funktionen zur Erzeugung von normalverteilten Zufallszahlen!
- Wie könnte man bessere normalverteilte Zufallszahlen finden?