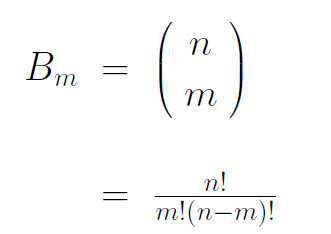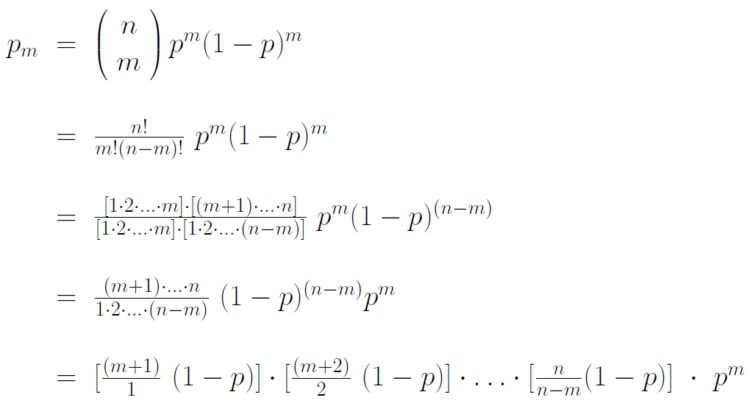Charly muss nun endlich Rike sein Problem mit der Binomialverteilung für die gymnasiale Oberstufe erklären. Er wundert sich nämlich, dass die Tabelle aus dem Schulbuch über die Sigma-1-Umgebung des Erwartungswertes gar nicht zum versprochenen Wert von 68,3 % für immer größere n konvergiert. Er ist wütend darüber.
Binomialverteilung
 | 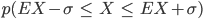 |
| 50 | 0.6877 |
| 100 | 0.6416 |
| 1 000 | 0.6829 |
| 10 000 | 0,6778 |
Binomialverteilung mit p=0.4 nach Bigalke/Köhler, Mathematik, 2020, S. 218.
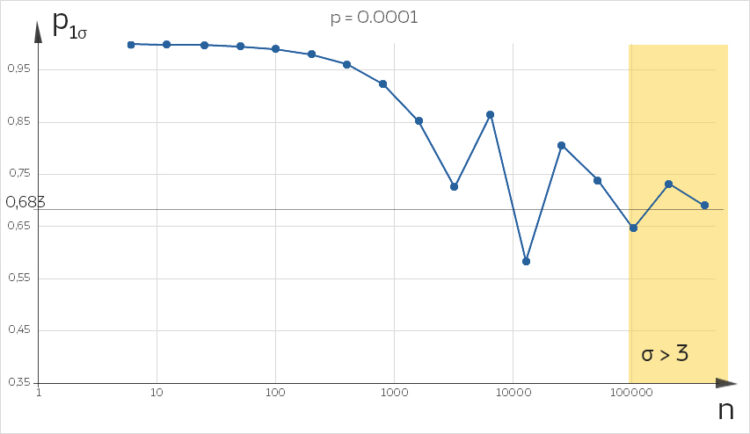
Charly Schau mal, Rike, diese Werte konvergieren nicht wenn n größer wird, sogar wenn die Sigma-Regeln erfüllt sind. Für n = 1 000 stimmt der Wert recht genau, für n=10 000 ist er ungenau, ein halbes Prozent Abweichung!
Rike Hey, Charly, du bist heute aber wütend.
Charly Jawoll, ich bin wütend. Ich habe versucht, das zu überprüfen. Mit einem Tabellenkalkulationsprogramm habe ich die Wahrscheinlichkeiten pm berechnet: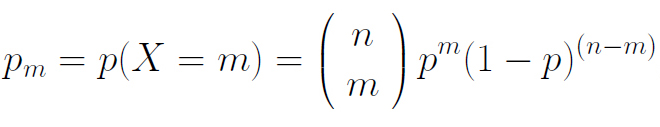 Doch die Binomialkoeffizienten sind so groß geworden, dass es da nicht mehr weiter ging.
Doch die Binomialkoeffizienten sind so groß geworden, dass es da nicht mehr weiter ging.
Rike Ja, richtig, das schaffen normale Programme mit 15 Stellen bis ca. n = 1 000.
Berechnung von Binomialkoeffizienten
Charly Ja, diese Koeffizienten Bm werden wegen der Fakultäten sehr groß:
Ich konnte alle Binomialkoeffizienten Bm für n = 1 000 berechnen. Für n = 1 248 aber nicht mehr. Im Tabellenkalkulationsprogramm war 10308 die größte Zahl.
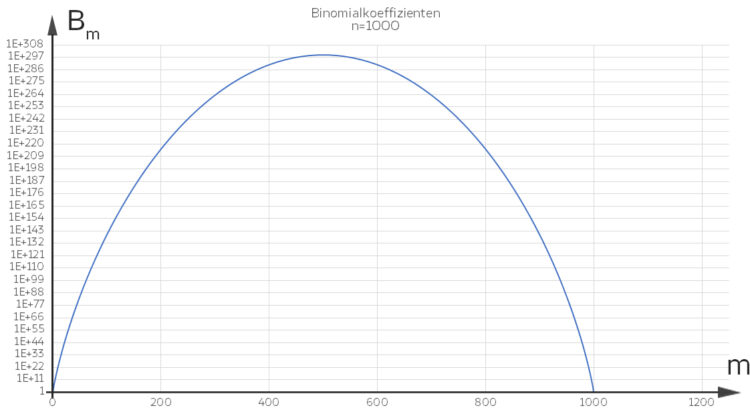
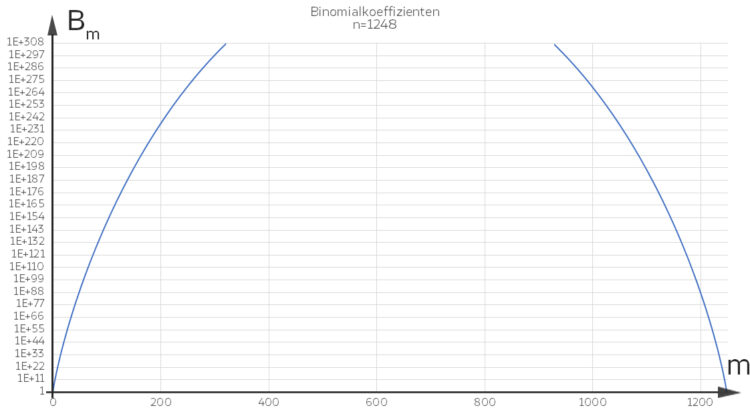
Rike Hmm. Deine Grafiken sehen gut aus.
Charly Danke!
Fakultäten mit CASION FX-87 DE X
Rike Eigentlich sollen wir im Unterricht einen wissenschaftlichen Taschenrechner benutzen. Beim Casio FX-87 DE X gibt es keinen Befehl für Binomialkoeffizienten. Wenn ich die Fakultäten berechnen will, dann geht das nur bis n = 69.

Rike Ha! Das ist ja nicht viel. Wie berechnet Casio die Wahrscheinlichkeiten pm der Binomialverteilung für große n?
Charlys Zweifel
Charly Für kleine n ist das ja möglich, für große nehmen sie vermutlich die Näherung durch die Normalverteilung, wie du es mir neulich erklärt hast. Jedenfalls habe ich keine Hinweise im Manual gefunden, wo die Berechnung für n = 10 000 herkommt. Großes Betriebsgeheimnis.
Rike Aha! Dir macht es wohl keinen Spaß, geheime Zahlen auszurechnen?
Charly No. Ich meine, ich unterrichte die Binomialverteilung ‒ und soll Werte benutzen, die nicht nachvollziehbar sind? Wo es nur um die Bedienung der Hard- und Software geht?
Rike Hmm, sehr schlecht. Es wird der Tag kommen, da benutzt ihr viel bessere Taschenrechner: mit größerem Display, mit intuitiver Bedienung, offener Programmierung, ordentlichem Manual...
Charly Ja, vielleicht schafft es sogar ein Smartphone, Binomialverteilungen auszurechnen.
Rike Das hoffe ich. Ein Tablet müsste es schon können.
Charly Na gut. Und jetzt?
Rikes Idee
Rike Ich habe da eine Idee... Diese Zahlen pm sind ja eigentlich Wahrscheinlichkeiten, also sie liegen zwischen 0 und 1:
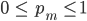
Vielleicht können wir sie geschickter berechnen? Mit Python?
Charly Ok, ja, lass uns das probieren.
Rike Also, wenn ich die Fakultäten auflöse, kürze, danach jeden Quotienten mit (1 ‒ p) multipliziere, dann dürfen doch die einzelnen Faktoren nicht so groß werden:
Mein Vorschlag wäre, für jedes m in einer Schleife den Faktor
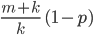
zu berechnen und solange an die vorläufige Zahl pm zu multiplizieren, bis wir fertig sind, das ist, warte mal, n ‒ m Mal. Am Ende kommt noch pm hinzu. Python lässt für ganze Zahlen beliebig große Werte zu, hat mir meine Schwester Paula erzählt und gezeigt, die kam weit über 10308.
Charly Cool.
Rike Weißt du, ich habe seit langem keinen Computer mehr angefasst, ich hatte keine Lust mehr…
Charly Ja, ich weiß. Dann probieren wir das zusammen.
Rike Okay, wir versuchen‘s ‒ weil du es bist.
Charly Danke!
Rike Zur Berechnung der 1-Sigma-Umgebungs-Wahrscheinlichkeit p1σ
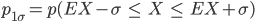
gehen wir alle m’s von 0 bis n durch. Wir testen, ob m in der 3-, 2- oder 1-Sigma-Umgebung liegt und rechnen nur für diese die Wahrscheinlichkeit pm aus. p1σ ist dann die Summe aller pm, die in der Umgebung liegen.
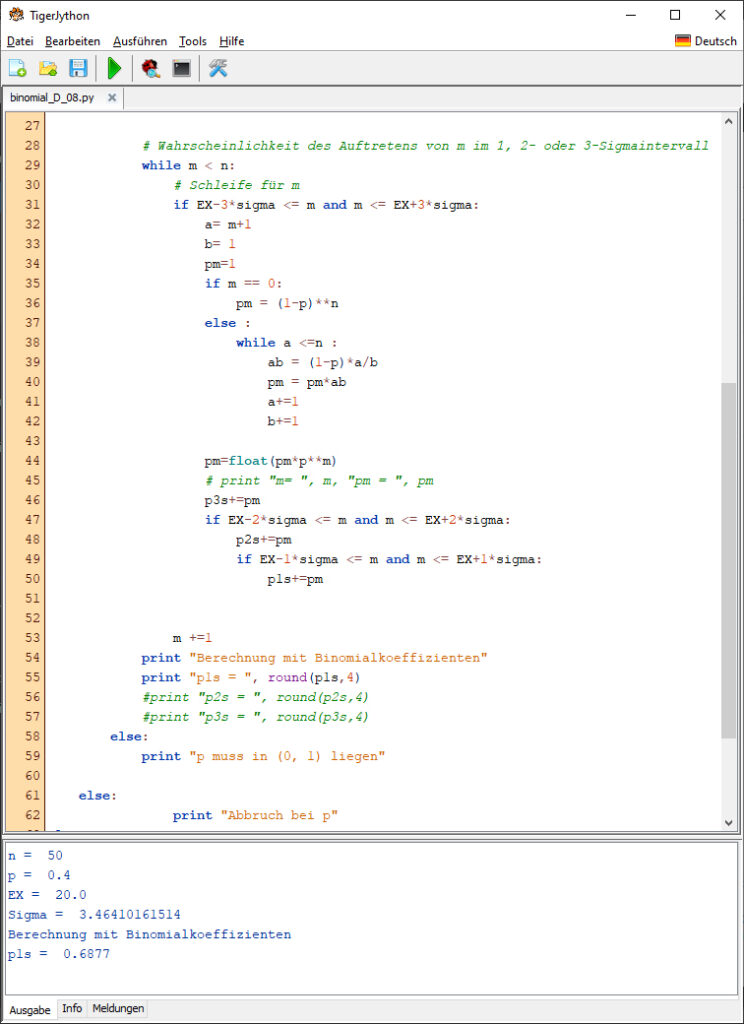
Charly Ganz ohne Näherung. Alles durch elementare Operationen. Super!
Rike Warte, einen Moment! Warum fängt denn die Tabelle in deinem Buch erst mit n= 50 an?
Charly Na, da ist die Sigma-Regel für p = 0.4 erfüllt,
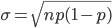
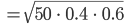
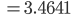
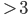
Ergebnisse mit Python
Rike Okay. Ich fange mal mit kleinen Zahlen an, da können wir die Werte mit jedem Rechner überprüfen. Hier, ich komme bis fast 2 000, aber dann ist mit Python auch Schluss:
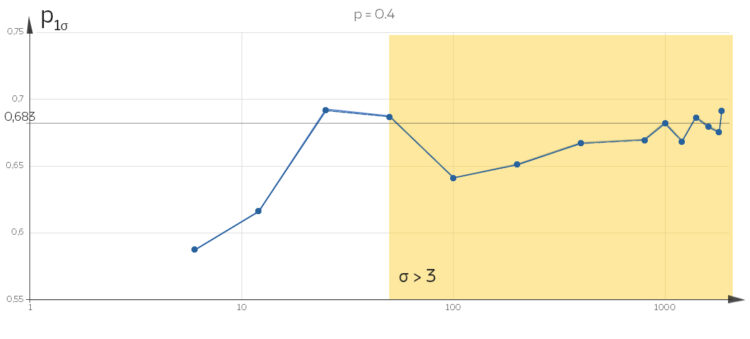
Charly Hey, Rike! Zeig mal! Du kannst bis 1 850 für p = 0.4 rechnen! Super! Das schaffen nicht mal alle Mathe-Portale.
Rike Danke! Die Werte aus dem Buch für n = 50, 100 und 1 000 kann ich bestätigen. Doch die Konvergenz zu dem Wert aus der Theorie der Normalverteilung 68,3 % ist noch nicht ersichtlich. Die Anzahl der Versuche n ist noch zu klein.
Charly das heißt, die Sigma-Regel
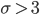
gewährleistet keine brauchbaren Ergebnisse?
Rike Stimmt, für n = 1 850 kriege ich
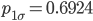
Charly Ist das nicht absurd! Da, wo die Werte vielleicht dem Näherungswert von 68.3 % genügen, können wir das nicht überprüfen. Da, wo wir p1σ ausrechnen können, ist die Näherung nicht genau genug. Ich glaub, ich drehe durch! Was soll ich tun?
Rike Du kannst das doch mit deinen Schülerinnen und Schülern diskutieren und selbst berechnen, Python ist eine tolle Programmiersprache, unsere Berechnung ist nachvollziehbar, sie hat nur elementare Operationen, wie du gesagt hast. Ist das nicht die Zukunft des Mathe- und Informatikunterrichts an der Schule?
Charly Hmm, ich glaube, du hast recht.
***
Übungsaufgabe
Berechne p1σ für andere Werte p.
Lösung