Rike besucht ihren „alten“ Freund Charly an diesem Wochenende. Charly wohnt inzwischen in Potsdam. Hier unterrichtet er Sport und Mathe. Mit den neusten Aufgaben zur Binomialverteilung hat er Schwierigkeiten.
Rike Hi, Charly, schön, dich wiederzusehen. Du siehst gut aus!
Charly Hi, Rike, schön, dass du gekommen bist. Wie geht es dir?
Rike Charly, wenn ich dich sehe, geht es mir gut. Ich freue mich, dass du nun in Potsdam bist!
Charly Ja, ich bin glücklich hier! Ich habe mich auf mehrere Stellen beworben, und hier in Potsdam hat es geklappt. In Brandenburg fehlen Mathelehrer, und an der Schule, an der ich jetzt bin, wird ja vor allem viel Sport getrieben, das gefällt mir. Ich kann sogar schon die Volleyballmannschaft mittrainieren.
Rike Hey, Charly, dann hast du es gut getroffen. Und Mathe? Kommst du klar?
Charly Ja, Rike, eigentlich ganz gut. Die Lehrer sind viel offener als an meiner alten Schule in der westfälischen Provinz, tatsächlich haben sich dort ein paar Mädchen in mich verliebt, du weißt schon, ich musste da weg. Hier sind die Jungs und Mädels richtig ehrgeizig und wollen alles genau wissen. Am besten, ich bette alles in sportliche Aufgaben ein.
Rike Haha.
Die Binomialverteilung
Charly Weißt du, Rike, nur mit einer Angelegenheit komme ich nicht klar: Wir behandeln in der 12 die Binomialverteilung, du weißt schon, ein Ereignis A tritt entweder ein oder nicht. Jeder Versuch ist unabhängig. Wenn das Eintreten von A die Wahrscheinlichkeit p hat, dann ist die Wahrscheinlichkeit, dass bei n Versuchen A genau m Mal eintritt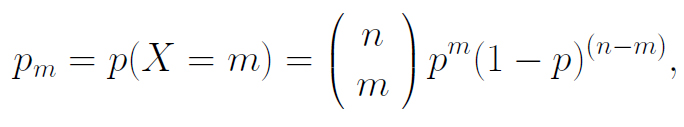
der Erwartungswert 
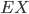ist:
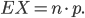
Die Standardabweichung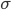 
ist
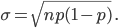
Ich nehme am liebsten das Ereignis, ob eine Mannschaft ein Spiel gewinnt oder verliert.
Rike Okay. n über m ergibt die Anzahl der Möglichkeiten, dass die Mannschaft m Mal gewinnt bei n Spielen, pm ist die Wahrscheinlichkeit für das Gewinnen von m Spielen und (1 - p)n-m ist die Wahrscheinlichkeit, n - m Mal zu verlieren. So weit, so gut.
Charly Ja, genau, so erkläre ich es. Doch es gibt in unserem Mathebuch Vorschriften, die fallen irgendwie vom Himmel.
Rike Ja?
Die Sigma-Regeln
Charly Die Sigma-Regeln, die gehen so: Wenn die Standardabweichung σ größer als 3 ist:
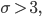
dann ist die Wahrscheinlichkeit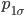 
, dass das Ereignis A in der 1-σ-Umgebung vom Erwartungswert EX liegt, 68.3 %.
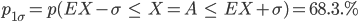
Für die 2-σ-Umgebung steht da 95.5 % und für die 3-σ-Umgebung 99.7 %.
Rike Das sieht ja ganz nach dem zentralen Grenzwertsatz von Moivre-Laplace aus. Der beschreibt grob gesagt, dass sich die Binomialverteilung für große n der gaußschen Normalverteilung (schwach) nähert. Dieser Satz hat natürlich einen Beweis. Doch die Bedingung
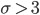
kommt darin nicht vor. Nur soll n sehr groß sein. Wenn n sehr groß ist, ist natürlich
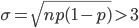
für festes p erfüllt. Hast du denn einen Beweis gefunden?
Charly Den suche ich noch. Im Mathebuch für die 12 steht keiner. Ich habe ein paar Beispiele gerechnet und kann das n i c h t in aller Gemeingültigkeit bestätigen! Rike, wo kommt so ein Satz her? Wie schafft es so ein Satz in ein Mathebuch für die Schule?
Rike Hmm, warte …, bei Wiki steht das auch – mit Quellenangabe. Jetzt besorge ich das Buch, das liegt ja online vor, und dann diskutieren wir das. Warte, eine Minute!
Charly Great! Rike, hast du schon die neuste Musik von Kae gehört?
Rike sitzt vor ihrem Notebook und antwortet nicht.
Charly Rike, willst du ‘nen Kaffee? Oder soll ich was kochen?
Rike Kaffee? Ja!
…
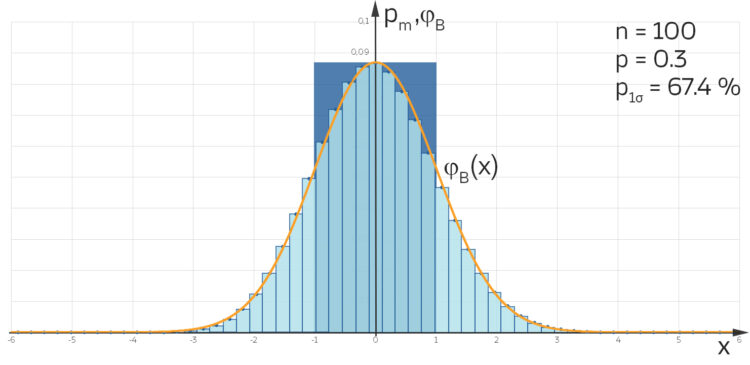
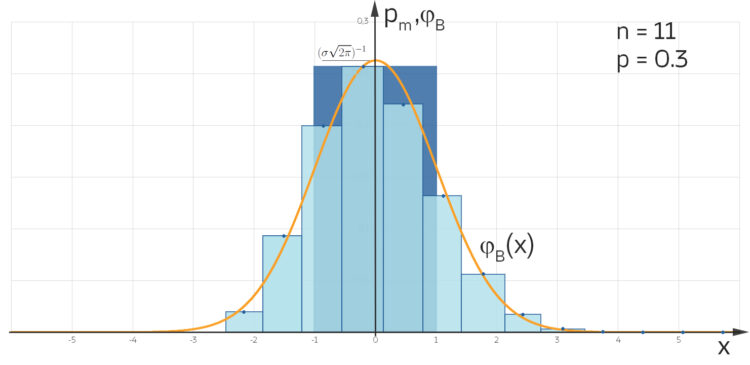
Histogrammdarstellung und 1-σ-Umgebung
Pass auf, du zeichnest die Wahrscheinlichkeiten pm über der Anzahl der Versuche m in ein sogenanntes Histogramm.
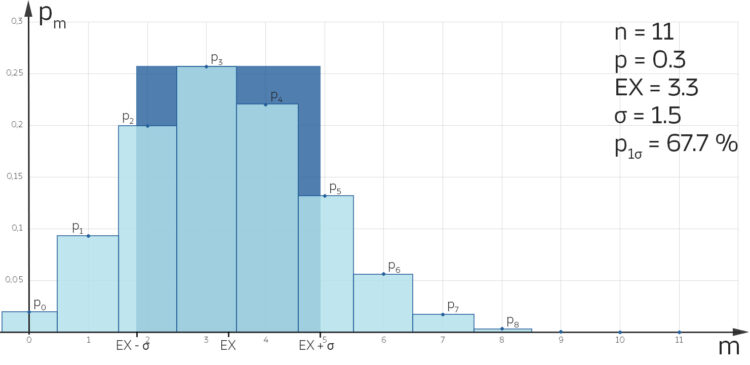
dargestellt in einem sogenannten Histogramm, in Dunkelblau die 1-σ-Umgebung dafür.Charly Okay.
Rike Für die Wahrscheinlichkeit, dass das Ereignis 
in einem Intervall 
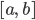liegt, musst du alle die Wahrscheinlichkeiten 
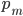addieren, für die m in diesem Intervall liegt:
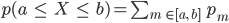
oder du berechnest die Fläche des Histogramms von a nach b. Das kannst du natürlich auch für die 1-σ-Umgebung so machen.
Charly Ja, ich weiß.
Lineare Substitution
Rike Der Autor dieser Sigma-Regel möchte gerne zeigen, dass diese Wahrscheinlichkeit ungefähr die Fläche unter der gaußschen Normalverteilung ist. Wenn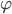 
die Dichte zur gaußschen Normalverteilung ist,
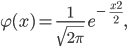
dann nähert sich die Binomialverteilung der Kurve
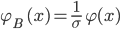
an, also der Normalverteilung mit einem Skalierungsfaktor. Dazu musst du allerdings deine m's in neue Veränderliche x umrechnen:
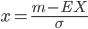
Das ist eine lineare Substitution. Wenn m kontinuierlich wäre, also wenn du fragen könntest, wie groß ist die Wahrscheinlichkeit, bei einem halben von n Spielen zu gewinnen…
Charly Hmm. Dann gibt es halbe und negative Anzahlen von Spielen???
Rike Tja, für die sportliche Interpretation musst du x wieder in m zurückrechnen.
Charly Haha! Sehr witzig.
Rike … das ist nicht so schwer. Weiter, aus der 1-σ-Umgebung
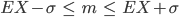
wird durch Subtraktion von EX auf allen Seiten:
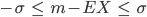
und schließlich durch Division durch σ:
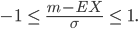
So haben wir jetzt in der Mitte x, das heißt
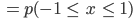
Charly Na gut, aber wo sind die Sigma-Regeln?
Die Faustregel
Rike Der Erfinder der Sigma-Regeln, Norbert Henze, argumentiert, dass wir statt der diskreten Wahrscheinlichkeiten 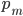die Kurve 
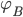benutzen können, solange die Histogrammfläche durch die Fläche unter der Kurve 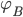gut approximiert werden kann. Er schreibt, die Approximation ist „brauchbar“, wenn
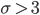
ist. Als „Faustregel“ gilt, wenn das Intervall von 0 bis 1 in mindestens 3 Teile zerlegt wird.
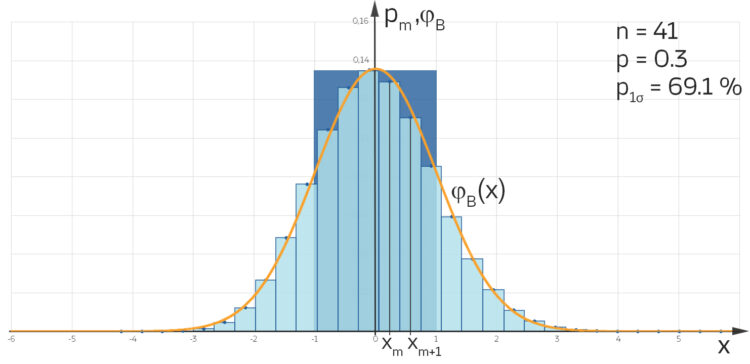
Charly Was? So ungefähr wie hier in deiner Abbildung? Ist das nicht sehr willkürlich?
Rike Ja, das ist es, er schreibt, es ist eine "Faustregel" für die "Praxis".
Charly Wahrscheinlichkeitsrechnung wird doch für die Praxis gemacht! Da sollte doch alles stimmen.
Rike Du bist aber wütend! Soll ich es dir bis zum Schluss erklären oder nicht?
Charly Ja, klar. Aber dann gehen wir raus. Ich zeige dir was.
Rike Gut. Lass mich raten. Spielen wir beide Beachvolleyball, eröffnen wir die Freibadsaison oder kennst du einen coolen Club?
Charly Das sind ja tolle Vorschläge, Rike. Lass dich überraschen.
Rike Also, wenn mindestens 3 Punkte 
im Intervall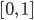 
liegen, dann ist
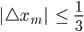
Charly Okay.
Rike Und wegen
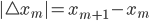
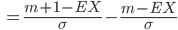
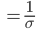
erhalten wir
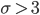
Charly So einfach? Komm, morgen zeige ich dir, warum ich das nicht gut finde, aber jetzt gehen wir, der Abend ist viel zu schön …
***
Übungsaufgabe
Berechne 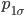für n=100, p = 0.3. Zeichne die Verteilungen.
Lösung
