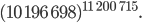Paula hatte mit Rike das Verschlüsseln mit dem RSA-Verfahren programmiert. Sie haben das flaubertsche Wort erection verschlüsselt und nrtciiie erhalten. Dazu mussten sie die Aufgabe
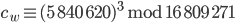
lösen. Die Berechnung hat weniger als 1 s gedauert. Doch viel aufwendiger ist die Dechiffrierung. Das wollen sie heute tun.
Den Private Key bestimmen
Paula Heute machen wir weiter mit dem Dechiffrieren. Ich will es gerne wissen.
Rike Ja, ich bin gespannt, wie du den Schlüssel zum Entschlüsseln ermittelst und ob es überhaupt klappt.
Paula Na, klar. Für den Private Key 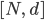 müssen wir
müssen wir 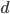 aus der Aufgabe
aus der Aufgabe
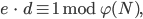
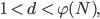
bestimmen.
Rike Wie machst du das?
Paula Ich gehe alle 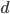 von 1 beginnend durch und teste, ob
von 1 beginnend durch und teste, ob
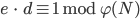
ergibt.
 und dem Private Key.
und dem Private Key.
Rike Okay! Dauert das lange?
Paula Warte, bei unserem
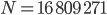
dauert das …, warte, hier, ich kriege
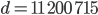
in 3 s.
Rike Wow! 11 Millionen!
Dechiffrieren
Paula Ja, 11 Millionen. Jetzt kommt die Entschlüsselung. Wir hatten das Wort
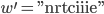
durch Verschlüsselung des Wortes
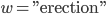
erhalten. Mit unserer Abbildung  von unserem Alphabet
von unserem Alphabet 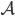
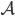 | 0 | c | e | i | n | o | r | t |
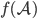 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
kriegen wie die Oktalzahl
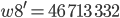
und dazu die entsprechende Dezimalzahl
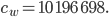
Das Dechiffrieren geht mit der Formel
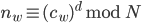
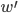 zu gegebenem Alphabet
zu gegebenem Alphabet 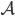 und
und  .
.
Rike Ja, ich weiß. Das Ergebnis wird bei uns sehr groß:
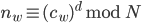

Kannst du das mit Python programmieren? Das macht kein Tabellenkalkulationsprogramm oder wissenschaftlicher Taschenrechner mit.
Große ganze Zahlen
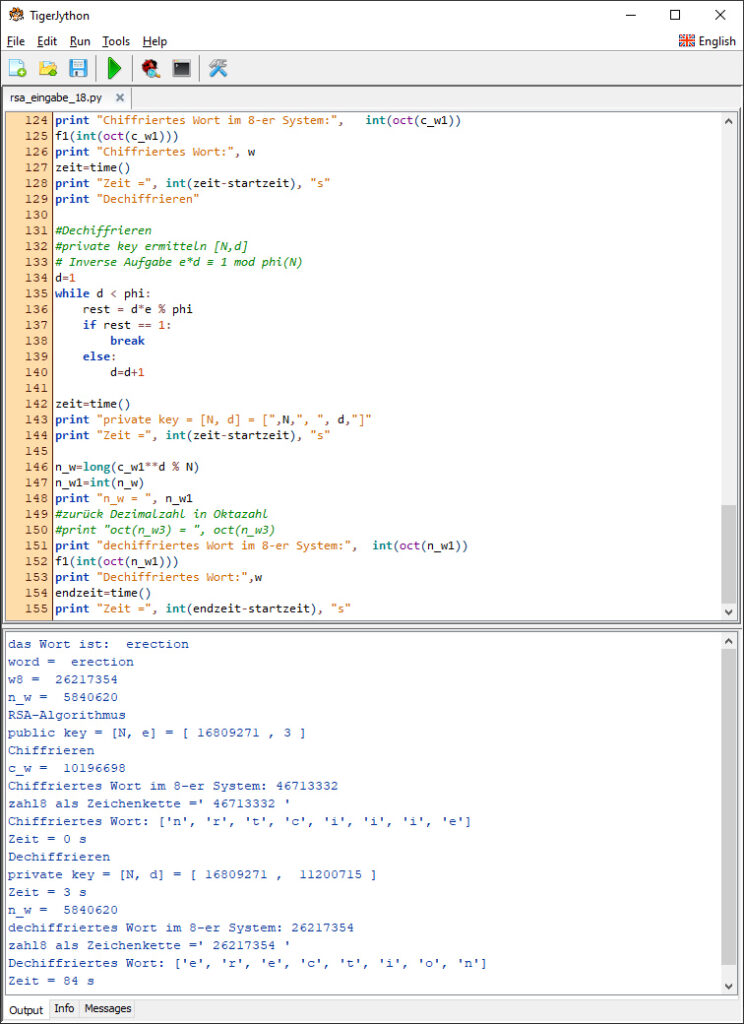
Paula In Python habe ich die Zahlentypen int und long für ganze Zahlen. Beide haben beliebig viele Stellen, es braucht nur Zeit und Arbeitsspeicher, um das zu berechnen.
Rike Okay, und wie lange braucht dein PC? Schafft er es überhaupt?
Paula Warte, ich brauche fürs Chiffrieren weniger als eine Sekunde, für die Bestimmung von 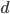 3 s und fürs Dechiffrieren 81 s. Einmal erection hin und zurück in 84 s.
3 s und fürs Dechiffrieren 81 s. Einmal erection hin und zurück in 84 s.
Rike Nicht schlecht! Kannst du mir mal diese Zahl
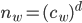
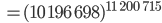
ausgeben?
Paula Ja, klar, warte, das muss ich eben noch codieren. Hier!
Rike Wie viele Stellen hat die?
Paula Warte, ca. 1 Million.
Rike Boah, das ist ja Wahnsinn! Wenn wir die Zahl hintereinanderschreiben, jede Ziffer mit Abstand zur nächsten vielleicht 4 mm breit, dann ergibt das eine Zahlenkette von der Länge 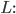
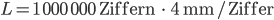
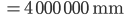
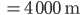
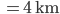
Das ist so viel wie 10 Mal ums Stadion laufen.
Paula Haha!
***
Übungsaufgaben
- Welches ist die letzte Ziffer von
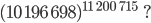
- Programmiere das RSA-Verfahren!
- Berechne