Rike fühlt sich wohl bei ihrer Schwester. Beide haben in München schon Einiges unternommen: Paula hat Rike den Campus in Garching gezeigt, beide haben Ragnar Axelssons Fotos bewundert, Rike war einmal bei einer Teambesprechung zu einem Game-Konzept dabei, abends haben sie die neusten Spiele gespielt... Für kurze Zeit vergessen sie ihre Sorgen: die steigenden Lebenshaltungskosten, der Krieg in der Ukraine, Zukunftsängste. Eigentlich wollte Rike niemals wieder eine mathematische Aufgabe lösen, doch mit Paula zusammen macht ihr das Diskutieren von mathematischen und Programmier-Themen wieder Spaß. Heute Abend wollen sie ihren RSA-Algorithmus fortsetzen.
Chiffrieren mit RSA nach Buchmann
Rike Jetzt bin ich gespannt, wie du Erection chiffrierst. Und vor allem, wie du es dechiffrierst, denn erst hier kommen die großen Zahlen ins Spiel.
Paula Na dann, lass uns das probieren. Also, wir haben ein Alphabet 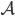 aus 7 Buchstaben und der Null:
aus 7 Buchstaben und der Null:
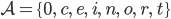
Das bilden wir mit unserer Funktion  auf
auf
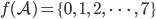
ab. Für das Wort
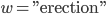
brauchen wir eine Blocklänge  von mindestens 8:
von mindestens 8:
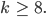
Rike Ja, ich weiß, das haben wir schon diskutiert.
Den Public Key bestimmen
Paula Beim RSA-Algorithmus geht man von einer natürlichen Zahl  aus, die Produkt von 2 verschiedenen Primzahlen ist:
aus, die Produkt von 2 verschiedenen Primzahlen ist:
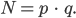
Aus dem  und der Länge des Alphabets
und der Länge des Alphabets  wird die Blocklänge berechnet:
wird die Blocklänge berechnet:
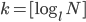
Rike Richtig. Jetzt haben wir
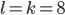
und müssen daraus das  bestimmen. Du weißt ja, dass
bestimmen. Du weißt ja, dass
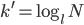
äquivalent ist zu
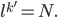
Paula Ja, das kann man als Umkehrfunktion sehen. Das hatten wir im 1. Semester! Aber der ganzzahlige Anteil?
Rike Der ganzzahlige Anteil einer Zahl ist kleiner oder gleich dieser Zahl:
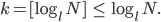
Außerdem ist der ganze Anteil einer Zahl echt kleiner als die nächste ganze Zahl:
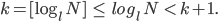
Weil der Logarithmus und das Abrunden monoton wachsende Funktionen sind, dann ist es die Umkehrfunktion auch! Wir haben dann
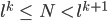
Paula Okay, dann kriegen wir
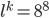
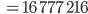
und
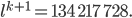
 soll ja Produkt von 2 Primzahlen sein, wenn die beide gleich wären, dann hätten wir
soll ja Produkt von 2 Primzahlen sein, wenn die beide gleich wären, dann hätten wir
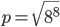
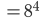
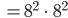
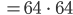
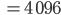
Natürlich sind 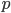 und
und 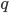 nicht gleich, aber so haben wir schon mal eine Abschätzung für
nicht gleich, aber so haben wir schon mal eine Abschätzung für 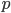 und
und 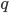 . Dann gehe ich die Liste der Primzahlen durch, warte mal, hier, … und finde
. Dann gehe ich die Liste der Primzahlen durch, warte mal, hier, … und finde
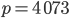
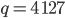
Das Produkt ergibt
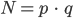
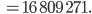
Rike Gut, die nehmen wir.  ist etwas größer als 88, das passt.
ist etwas größer als 88, das passt.
Paula Jetzt berechne ich die eulersche Phi-Funktion für  . Weil
. Weil 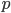 und
und 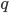 Primzahlen sind, ist das einfach:
Primzahlen sind, ist das einfach:
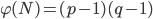
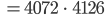
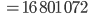
Rike Okay.
Paula Jetzt kann ich den Public Key berechnen, der enthält alle Informationen zum Chriffrieren. Wir brauchen nur ein natürliches  zu wählen, das zwischen 1 und
zu wählen, das zwischen 1 und 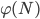 liegt und teilerfremd zu
liegt und teilerfremd zu 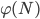 ist:
ist:
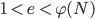
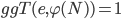
Rike Ich glaube, 3 ist das kleinste  .
.
Paula Schön, dann haben wir den Public Key:
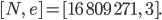
Chiffrieren von Wörtern
Jetzt können wir alle Wörter aus unserem Alphabet und natürlich auch Flauberts Erection verschlüsseln. Aus dem Wort
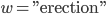
berechnen wir die Zuordnung
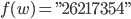
als Zeichenkette und daraus die Oktalzahl
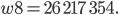
Diese Zahl stellen wir als Dezimalzahl dar und benutzen die Standardbezeichnung  mit dem Index
mit dem Index 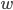 für die Abhängigkeit vom Wort
für die Abhängigkeit vom Wort 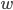 , eben
, eben 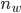 . Das hatten wir ja schon programmiert, das ergibt
. Das hatten wir ja schon programmiert, das ergibt
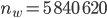
Diese Zahl 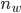 wird so verschlüsselt:
wird so verschlüsselt:
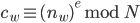
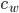 ist die chiffrierte Zahl im Dezimalsystem. Die bringen wir noch ins Oktalsystem und bilden sie mit unserer Umkehrabbildung zu
ist die chiffrierte Zahl im Dezimalsystem. Die bringen wir noch ins Oktalsystem und bilden sie mit unserer Umkehrabbildung zu  ins Alphabet ab.
ins Alphabet ab.
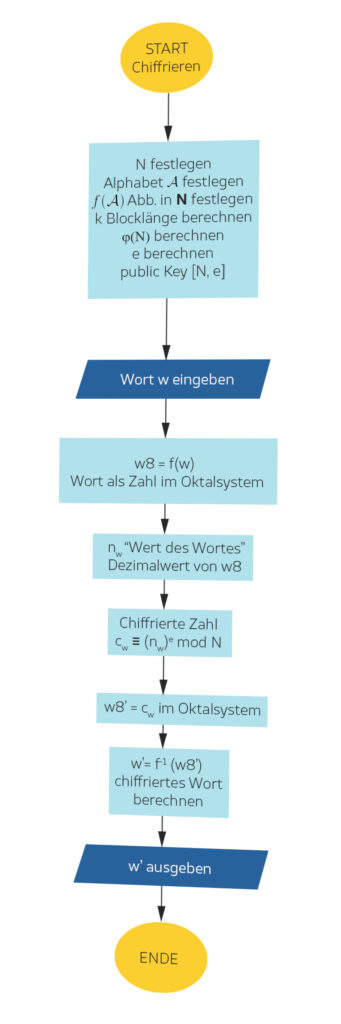
Rike Sag, mal, das kannst du doch ganz straight forward programmieren?
Paula Ja,klar, das ist eine lineare Abfolge, genau wie ich‘s erklärt habe:
Rike Verstehe ‒ und was kommt raus?
Paula Warte, one moment, hier, das chiffrierte Wort ist
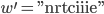
Rike Witzig! Kannst du das französisch aussprechen?
Paula Nö, dreifache I gibt es da nicht. Rike, was hätte Flaubert dazu gesagt?
Rike Du hättest ihm bestimmt gefallen, er mag Frauen: Frauen, die tanzen, singen und sich ausziehen, aber auch Frauen, die sich leidenschaftlich mit einer Sache beschäftigen. Nur das Alphabet aus 7 Buchstaben, das hätte ihm bestimmt nicht gefallen, er war gegen jede Art von Reglementierung.
Paula Hmm, vielleicht lese ich auch mal was von ihm. Wenn mein RSA-Algorithmus fertig ist, kann ich ihn ja auf alle Buchstaben des französischen Alphabets erweitern, Python kennt da keine Grenzen!
Rike Super! Das hört sich gut an.
Fortsetzung folgt hier.
***
Übungsaufgabe
Programmiere selbst die Verschlüsselung und überprüfe das Ergebnis.
