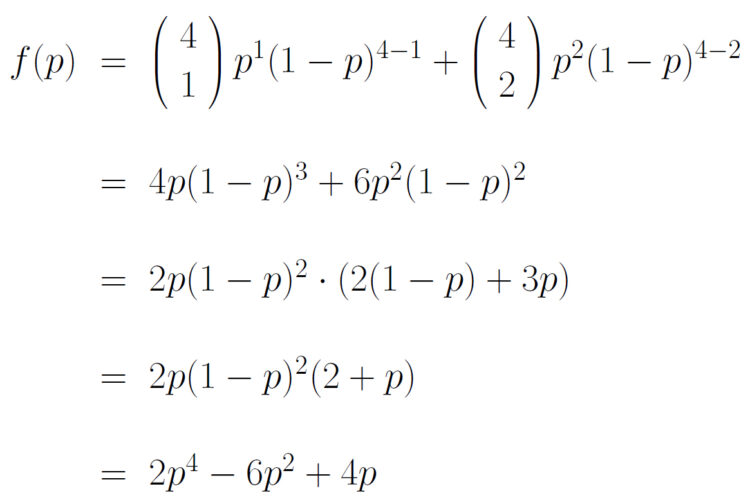Rike und Charly diskutieren eine ehemalige Abiaufgabe zur Binomialverteilung.
Rike Mir ist in eurem Lehrbuch aufgefallen, dass die kumulative Binomialverteilung als Histogramm gezeichnet wird. Ist das nicht irreführend?
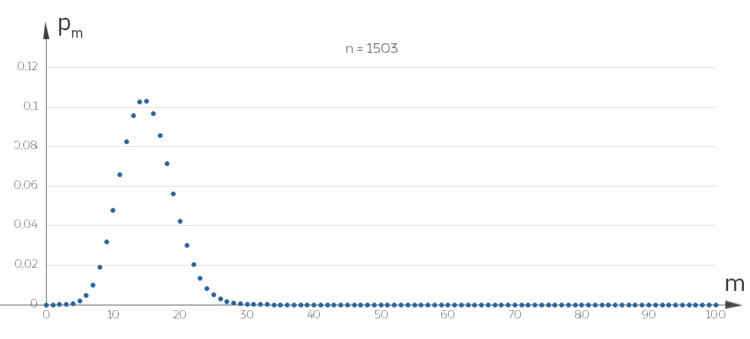
Kumulative Binomialverteilung
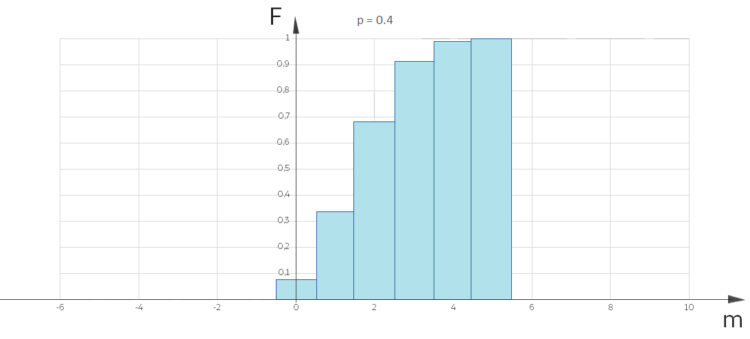
Charly Ja, da hast du recht. Manchmal ist Didaktik stärker als Mathematik. Die kumulative Binomialverteilung wird nicht klar definiert.
Rike Warum das denn nicht? Sollte sie nicht wie alle Verteilungen von Zufallsgrößen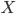 
auf ganz 
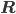definiert sein?
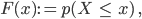
egal, ob 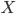diskrete oder kontinuierliche Werte annimmt.
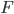hat außerdem die typischen Eigenschaften einer Verteilungsfunktion:
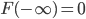
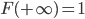
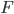- ist monoton wachsend
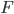- ist stetig von rechts
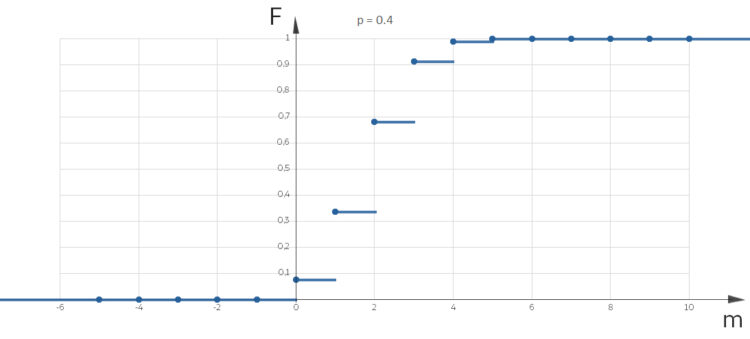
Sollte das nicht jede Abiturientin und jeder Abiturient wissen?
Berechnung mit dem wissenschaftlichen Taschenrechner (Casio)
Charly Da sagst du was. Natürlich können wir das im Unterricht klarstellen und behandeln, doch der wissenschaftliche Taschenrechner macht das anders. Er lässt für die kumulative Binomialverteilung zwar negative Werte zu, aber sonst nur ganzzahlige.
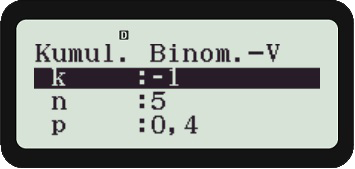
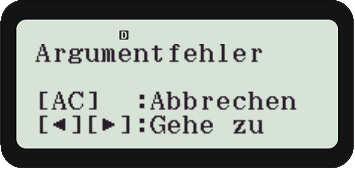
Rike Ach Gott! Wer hat hier wen beeinflusst?
Charly Haha, das ist doch offensichtlich. Manchmal können Denken in Sachzusammenhängen, Bequemlichkeit oder Geld sogar mathematische Theorien ändern.
Rike Und du?
Charly Nächste Frage!
Rike Kommen Aufgaben mit der kumulativen Binomialverteilung beim Abi vor?
Charly Bis jetzt habe ich nur eine Aufgabe dazu gefunden. Glücklicherweise geht die nicht direkt auf die Definition der Funktion ein, die Funktion wird nur symbolisch berechnet also ohne wissenschaftlichen Taschenrechner.
Rike Ach ja? Dann zeig doch mal!
Die Zahnarztaufgabe
Charly Die Aufgabe ist von 2015. [Bildungsserver Berlin-Brandenburg, 2015, S. 9]
Zentrale schriftliche Abiturprüfung 2015 Länder Berlin und Brandenburg
Aufgabe 3.2 CAS: „Vorsorgemuffel“
Zu „Vorsorgemuffeln“ zählen Bundesbürger, die nicht regelmäßig eine Zahnarztpraxis zu Kontrolluntersuchungen aufsuchen. Nach einer Umfrage des Instituts der Deutschen Zahnärzte (2013) zählen dazu 29,3 % der weiblichen und sogar 44,7 % der männlichen Bundesbürger.
Unabhängig davon, ob er ein „Vorsorgemuffel“ ist oder nicht, geht im Mittel jeder sechste Bundesbürger bei akuten Beschwerden sofort zu einem Zahnarzt.
Wenn nicht ausdrücklich von männlichen oder weiblichen Bundesbürgern die Rede ist, sind immer alle Bundesbürger unabhängig vom Geschlecht gemeint.[…]
e) In einem Landesteil Deutschlands beträgt die Wahrscheinlichkeit dafür, dass ein Einwohner „Vorsorgemuffel“ ist, p mit 0 < p < 1.
Berechnen Sie p für den Fall, dass die Wahrscheinlichkeit dafür, dass sich unter vier zufällig ausgewählten Einwohnern dieses Landesteiles ein oder zwei „Vorsorgemuffel“ befinden, maximal ist.
Modellierung
Rike Haha, was ist denn das für eine Frage? Wollen die Zahnärzte das wirklich wissen?
Charly Nein, ich glaube nicht. Ich habe versucht, die genannte Studie zu finden, doch sie ist nicht online. Dafür habe ich eine Studie des Instituts der Deutschen Zahnärzte zur Behandlung jüngerer Kinder von 2013 und den Geschäftsbericht 2013/2014 der Kassenzahnärztlichen Bundesvereinigung gefunden. Zahnarztmuffel kommen darin nicht vor. Auch geht es um die Zahnärzte selbst, die werden befragt, nicht die Patienten und Patientinnen. Ich fand die Studien sehr interessant und seriös, aus dem Material könnte man ein paar gute Statistikaufgaben kreieren…
Rike Hmm, okay, Charly, bevor du an die entscheidenden Stellen wechselst, lass uns kurz vorher noch diese Aufgabe lösen. Oder ist sie nicht lösbar?
Charly Klar, die ist lösbar. Zuerst sagen wir, dass 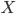die zufällige Anzahl von „Vorsorgemuffeln“ in einer Stichprobe mit 
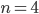beschreibt. Wir definieren eine Funktion 
:
die beschreibt eine Wahrscheinlichkeit, deshalb sind die Ergebnisse zwischen 0 und 1, außerdem hängt von der Wahrscheinlichkeit 
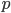− ein Einwohner ist „Vorsorgemuffel“ − ab, deshalb ist das Argument auch zwischen 0 und 1. Die Funktion geht so:
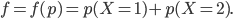
soll maximal werden.
Rike Sag‘ mal, ist das nicht eine Analysis-Aufgabe?
Charly Eigentlich schon. Sowas nennt sich komplexe Aufgabe.
Rike Haha! Sehr witzig.
Charly Soll ich mal?
Rike Na los!
Charly Also, wegen der Binomialverteilung ist
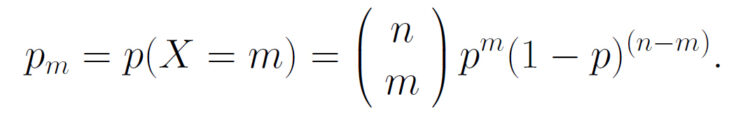
Das benutzen wir, setzen n = 4 und ich versuche das mal in einzusetzen:
Minimax-Aufgabe
Rike Cool, schön, dass du erst mal als Produkt geschrieben hast, da sieht man, dass
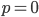
und
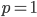
eine Sonderrolle spielen. Aber für die 1. Ableitung ist die Produktdarstellung nicht so gut.
Charly Stimmt. Aber mit der Summe geht es gut:
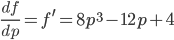
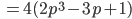
Das soll nun Null werden.
Rike Hmm, etwas schwierig, ein Term 3. Ordnung!
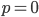
ist keine Lösung, aber
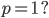
Charly Ja, mit 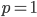kriegen wir
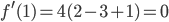
Rike Gut, das hilft uns weiter!
Charly Dann kann ich die 1. Ableitung durch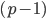 
teilen:
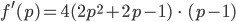
Rike Jetzt nur noch die p-q-Formel für das quadratische Polynom – und wir haben das Maximum oder Minimum.
Charly Okay,
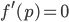
genau dann, wenn
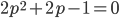
oder
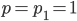
genau dann, wenn
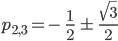
oder
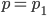
Die 2. Nullstelle ist
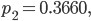
die 3. Nullstelle ist negativ und entfällt bei uns.
Jetzt berechne ich an dieser Stelle:
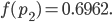
Offensichtlich liegt bei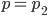 
ein Maximum vor.
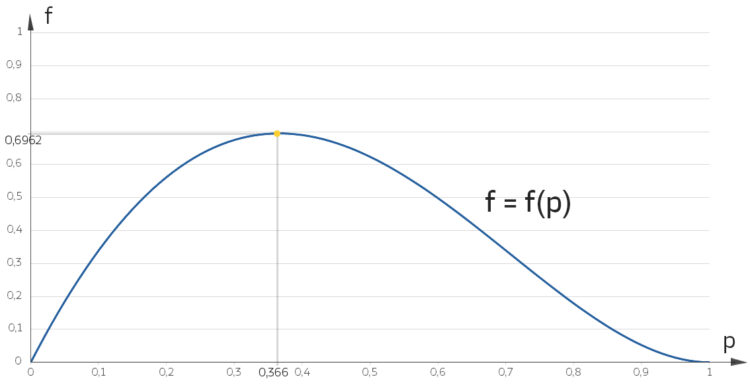
Das Ergebnis als 1-Sigma-Umgebung
Rike Dann hast du die 5. Teilaufgabe gelöst, die Wahrscheinlichkeit, dass 1 oder 2 „Vorsorgemuffel“ unter 4 Einwohnern sind, wird maximal, und zwar 69.62 %, wenn 36.6 % der Einwohner „Vorsorgemuffel“ sind. Das ist ungefähr der Wert aus den Daten für Männer und Frauen gemittelt. Das gibt keine neue Information. Aber die 69.62 % sehen wie eine 1-Sigma-Umgebungswahrscheinlichkeit aus. Was meinst du?
Charly Hmm, das kann ich testen. Bei der Binomialverteilung mit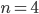 
und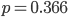 
haben wir den Erwartungswert 
:
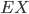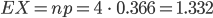
und dazu die Standardabweichung
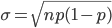
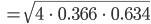
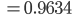
Die 1-Sigma-Umgebung ist dann das Intervall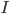 
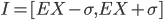
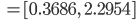
Wenn wir nun ganzzahlige Zufallsgrößen zulassen, wie hier die Anzahl der Testpersonen, dann ist
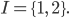
Rike Stimmt, gerade bei diesen beiden Werten ist die Wahrscheinlichkeit am größten, weil sie nahe des Erwartungswertes liegen. Das passt schon.
Charly Die Aufgabe wurde rückwärts entworfen. So eine kleine Testgruppe!
Rike Vergiss es, Charly, welches sind nun deine Alternativaufgaben?
Charly Na, zuerst würde ich ein Tabellenkalkulationsprogramm zulassen. Diese wissenschaftlichen Taschenrechner sind nicht mehr der Industriestandard für solche Aufgaben. Heute könnte man solche Aufgaben mit einem kleinen digitalen Endgerät lösen. Innerhalb des Abiturs muss die Internetverbindung natürlich deaktiviert sein.
Rike Ja klar. Das war in meinem Studium auch schon so.
Charly Jetzt kommt meine alternative Abi-Aufgabe:
Charlys alternative Abiaufgabe
Im kassenzahnärztlichen Geschäftsbericht von 2013/14, S.10 steht, dass weniger als 1 % der Erwachsenen ein kariesfreies Gebiss haben. Sagen wir mal 1 %. Nehmen wir noch außerdem an, alle Abiturienten sind erwachsen. Lass uns einen oder eine Abiturient:in unter unseren 20 teilnehmenden Abiturient:innen auswählen.
- Wie groß ist die Wahrscheinlichkeit, dass bei dieser Auswahl mindestens ein/e Abiturient:in ein kariesfreies Gebiss hat?
- Wie groß ist die Wahrscheinlichkeit, dass eine bestimmte Person ausgewählt wird – zum Beispiel du – und keine Karies hat?
- Wie groß sind die 1-Sigma-Wahrscheinlichkeit und die 1-Sigma-Umgebung?
- Jetzt wählen wir eine größere Testgruppe: die Erwachsenen in Potsdam. Wir nehmen an, dass in Potsdam wie in Deutschland 83.5 % von den ca. 180 000 Einwohner:innen erwachsen sind. Wie groß sind jetzt die 1-Sigma-Wahrscheinlichkeit und die 1-Sigma-Umgebung?
- Wir wählen für eine repräsentative Stichprobe 1 % der erwachsenen Potsdamer:innen aus. Wie groß sind jetzt die 1-Sigma-Wahrscheinlichkeit und die 1-Sigma-Umgebung?
- Zeichne die Wahrscheinlichkeitsdichte dafür!
Rike Nicht schlecht! Charly, ich putze meine Zähne. Wollen wir mal was anderes machen als über Zähne zu sprechen?
Charly Ja, komm.
***
Übungsaufgabe
Löse Charlys Aufgabe!
Lösungen
- 18.20 %
- 0.05 %
- EX = 0.2, σ = 0.4450, I = [-0.250; 0.6450] ~ [0; 0], k = 0, p1σ = 81.79 %
- EX = 1 503, σ = 38.57, I = [1 464.43; 1 541.57] ~ [1 465; 1 541], p1σ = 68.27 % (Näherung durch Normalverteilung) bzw. p1σ = 68.18 % (Casio)
- EX = 15.03, σ = 3.85, I = [11.18; 18.88] ~ [12; 18], p1σ = 63.70 %
