Nachdem das Erzeugen von fotorealistischen Bildern mit konkreten Vorgaben mittels AI so schief gelaufen ist, hat Rike eine andere Teststrategie. Sie will testen, wie intelligent die „Künstliche Intelligenz“ wirklich ist. So viele intelligente Algorithmen, so viel Mathematik, was versteht die „Künstliche Intelligenz“ wirklich von Mathematik? So gibt sie probeweise ihr „altes“ Bild von einigen Sinus- und Kosinus-Funktionen ein. Diese bilden ein Orthonormalsystem, gerade das hat sie damals Ben erklärt. Die Darstellung von 2π-periodischen, quadratisch integrierbaren Funktionen als Summe von solchen Schwingungen heißt Fourier-Reihe. Das ist ein wichtiges mathematisches Konzept, in Funktionen Schwingungen zu finden und zu benutzen. Es hat viele technische Anwendungen. Rike fragt sich, ob DALL.E diese Schwingungen erkennen und intelligent variieren kann.
Variantionen von Schwingungen
Sie wählt das folgende Ausgangsbild:
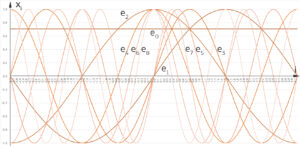
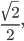
Aus diesem muss sie einen quadratischen Ausschnitt festlegen, da DALL.E nur quadratische Bilder verarbeitet. Da das Bild nur ca. 1000 px hoch und breit ist, will sie das Bild nicht verkleinern und oben und unten Weißraum dazugeben, sondern schneidet das Bild rechts ab, die Schwingungen sind immer noch gut zu erkennen.
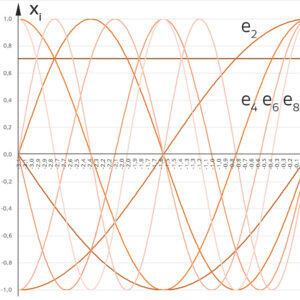
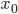
Sie gibt dieses Bild 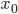 in DALL.E ein und lässt es variieren. Da kommt Charly gerade vom Volleyball-Training zurück und schaut ihr über die Schulter. Als sie die folgenden Ergebnisse erhält, wundern sie sich und lachen.
in DALL.E ein und lässt es variieren. Da kommt Charly gerade vom Volleyball-Training zurück und schaut ihr über die Schulter. Als sie die folgenden Ergebnisse erhält, wundern sie sich und lachen.
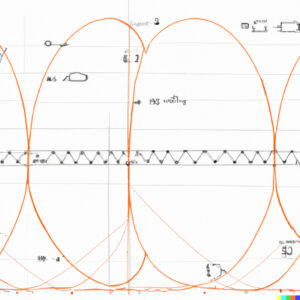
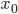 von DALL.E erzeugt
von DALL.E erzeugt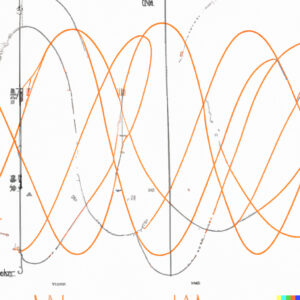
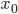 von DALL.E erzeugt
von DALL.E erzeugt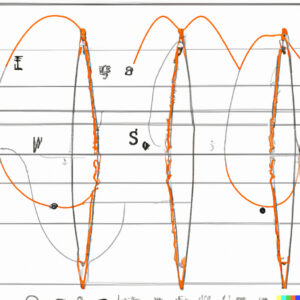
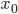 von DALL.E erzeugt
von DALL.E erzeugt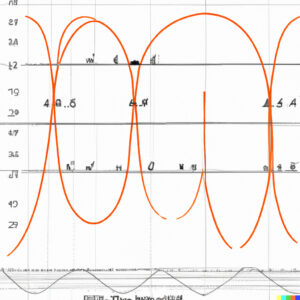
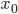 von DALL.E erzeugt
von DALL.E erzeugtCharly Ha, die Bilder sehen sehr witzig aus, irgendwie knuffig, wie ein Mädchenpo!
Rike Haha! Du hast Recht, die Bilder sehen frisch, leicht und kreativ aus. Doch von den Sinus- und Kosiunsfunktionen und dem typischen Fourier-Ansatz ist nicht viel zu erkennen, nur beim 2. Bild. Im 1. und 4. Bild werden Schwingungen dekorativ, also klein, in Schwarz/Weiß, wie ein zusätzliches grafisches Element verwendet.
Charly Was ist denn aus der Schrift geworden? Aus der Achsenbezeichnung, den 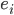 ’s, dem
’s, dem 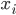 ?
?
Rike Das ist so ein typisches Merkmal von DALL.E, dass ein eingebetteter Text so variiert wird, dass er wenig Sinn ergibt oder unlesbar wird. Jedes der 4 Bilder hat andere Zeichen, vermutlich sind die zufällig erzeugt.
Charly Alle Namen, Bezeichnungen, Logos werden unkenntlich gemacht? Sieht ganz nach einer Vermeidung von Urheberrechtsproblemen aus.
Rike Jaja, sieht ganz so aus.
Charly Wie entstehen solche Bilder? Hast du eine Ahnung?
Rike Ich bin dabei, das zu verstehen. Eine Methode ist die zufällige Variation von Teilen des Originalbildes und das Aufgreifen des Stils. Eine andere Möglichkeit berechnet neue Bilder durch Interpolation des Ausgangsbildes mit einem weiteren Bild. Dieses weitere Bild könnte aus einer Datenbank oder aus einer Variation entstehen.
Interpolation
Charly Aha! Wie stelle ich mir so eine Interpolation vor?
Rike Nehmen wir mal das 2. Bild und nennen es 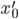 , um anzudeuten, dass es aus
, um anzudeuten, dass es aus 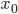 entstanden ist. Das könnte aus einer Interpolation entstanden sein, weil es große Ähnlichkeit in Form und Farbe mit dem Original hat.
entstanden ist. Das könnte aus einer Interpolation entstanden sein, weil es große Ähnlichkeit in Form und Farbe mit dem Original hat.
Charly Gut! Und weiter?
Rike Wir nehmen mal Buchstaben und Bezeichnungen überall raus, so gut es geht, und natürlich auch das DALL.E-Logo im finalen Bild. „Texte“ und Logos werden am Ende eingefügt.
Charly Verstehe!
Rike Wir überlagern das Bild 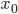 mit dem Bild
mit dem Bild 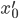 linear:
linear:
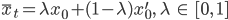
Tatsächlich ist 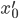 nicht das Endbild der Interpolation, das kenne ich nicht. Aber ich kann dir erklären, wie aus diesen beiden Bildern neue entstehen.
nicht das Endbild der Interpolation, das kenne ich nicht. Aber ich kann dir erklären, wie aus diesen beiden Bildern neue entstehen.

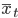 : Am Anfang ist das Ausgangsbild
: Am Anfang ist das Ausgangsbild 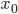 , am Ende das Bild
, am Ende das Bild 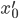 mit
mit 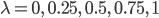
Charly Hmm, ziemlich kompliziert, doch ich glaube, ich verstehe.
Rike Bei der Überlagerung von Bildern werden die Bilder mit verschiedener Durchsichtigkeit übereinandergelegt. So sieht man beide Bilder gleichzeitig. Bei unseren Schwingungsmotiven mit vielen Linien wirken die Überlagerungsbilder recht unübersichtlich. Bei anderen Motiven, nicht mathematischen, zum Beispiel bei Gesichtern erkennt man eins von beiden mehr als das andere. Doch das Übergangsbild schafft noch kein neues Bild, keine neue Struktur, keine neue Information. Aus solch einem Überlagerungsbild sollte ein „intelligentes“ Bild „künstlich“ entstehen, welches Merkmale beider hat, aber ein eigenständiges Objekt darstellt, ein neues Gesicht quasi.
Charly Verstehe. Ist ja krass. Das ist genau der Punkt. Und wie geht das?
Das Diffusionsmodell
Rike Durch Hinzugeben von Rauschen versucht man, die weniger wesentlichen Details zu unterdrücken. Die wichtigen Details bleiben erkennbar.
Charly Na gut.
Rike Aus diesen wenigen kaum erkennbaren Details wird mittels AI das Rauschen wieder entfernt.
Charly Kommt denn da nicht das Ausgangsbild wieder heraus? Oder wenigstens das stark reduzierte?
Rike Nicht ganz. Die AI wird so trainiert, dass für jeden „wichtigen“ Pixel ein Pixel gesucht wird, aus dem dieser hervorgegangen sein könnte. Quasi das umgekehrte Anfangswertproblem. Da steckt viel Zufall drin und bei jedem Denoising-Verfahren kommt was anderes raus.
Charly Hmm, kann ich mir das so vorstellen wie beim Volleyball? Wenn ein Ball bei einem Spieler ankommt, hat er zwar eine Geschwindigkeit und ein Drehmoment, sodass ich seinen Weg zurückverfolgen kann, aber das ganze Spiel schaffe ich doch nicht zurückzuverfolgen oder auch vorauszusagen. Das schafft nicht mal ein richtige Volleyballintelligenz, haha.
Rike Ja, so ungefähr, nur für das Rauschen haben wir keine Metapher.
Charly Das macht nichts. Jetzt sag mir noch, was ein „wichtiger“ Pixel ist! Das muss ja irgendwie berechenbar sein?
Rike Ja, das ist einer mit starken Änderungen relativ zu seinen Nachbarn in Farbe und Helligkeit.
Charly Okay, jetzt zeig mir doch noch mal ein Zwischenbild!
Rike Okay, nehmen wir mal die 50-50-Überlagerung beider Bilder. Zu diesem Bild füge ich Rauschen in vielen kleinen Schritten hinzu, und zwar solches Rauschen, das das Bild sehr wenig ändert, also mit einem sehr guten Signal-Rausch-Verhältnis. Bei Ho et al. nehmen sie maximal 1.000 Schritte, die Varianz wächst bei ihnen von 0.0001 bis 0.02. Bei mir ist es das Gaußsche Rauschen mit 1 % Was-auch-immer in Photoshop.

Charly Okay, doch das Denoising ist das Interessanteste.
Rike Ich habe so viele Einzelbilder, ich kann sogar ein Video daraus machen.
Charly Na los!
Charly Okay, nicht schlecht! Kannst Du auch simulieren, was aus den anderen beiden 25-75- und 75-25-Überlagerungen rauskommt?
Rike Na klar! Hier:

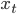 von
von 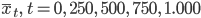 sein könnten, umgekehrter stochastischer Prozess.
sein könnten, umgekehrter stochastischer Prozess.Charly Cool, Rike! Vielleicht kannst du ja doch ein Volleyballspiel zurückberechnen oder noch besser: vorausberechnen?!
Rike Haha!
***
Übungsaufgaben
- Teste selbst Variationen mathematischer Abbildungen!
- Kann aus einem verrauschten Überlagerungsbild jedes Bild durch Denoising entstehen?
Lösung
2. Nein, beispielsweise müssen die mittleren Helligkeiten und mittleren Farbwerte des Ausgangs- und Zielbildes übereinstimmen.
