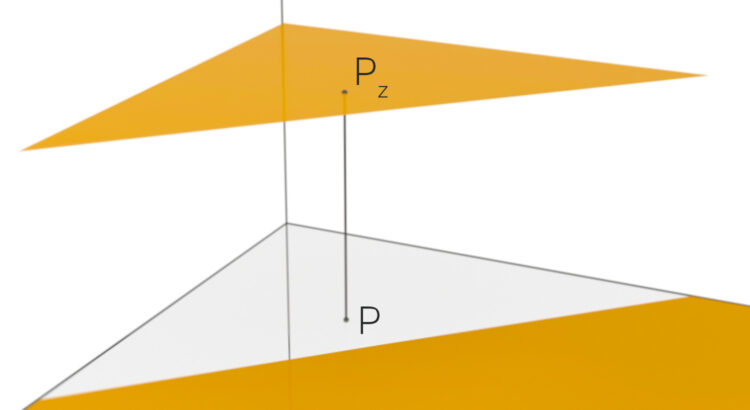
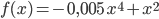Rike kommt für einen kurzen Besuch an ihre ehemalige Uni, wo sie früher Mathetutorien gegeben hat. Sie lässt sich die neusten Matheklausuren zeigen. Die von der 3D-Darstellung von Funktionen zweier Veränderlicher hat es ihr besonders angetan. Wie schön die ist, seufzt sie.

Charlys Lösung der IGA-Aufgabe
Charly wundert sich, dass Rikes "seriöse" Lösung der IGA-Abiaufgabe ein anderes Ergebnis als die Musterlösung liefert. Rike hat ein regelmäßiges Muster, das die Anforderung von 6 Blumen pro m² erfüllt, gefunden und damit die gegebene Fläche  zwischen den Kurven
zwischen den Kurven 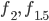 und der
und der  -Achse von knapp 30 m² ausgelegt.
-Achse von knapp 30 m² ausgelegt.
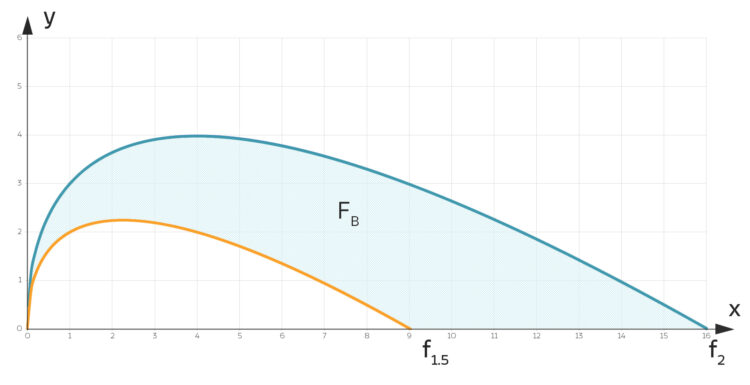
 , die mit Blumen zu belegen ist. Für die Formeln von
, die mit Blumen zu belegen ist. Für die Formeln von 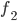 und
und 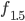 siehe Beitrag Die IGA-Aufgabe.
siehe Beitrag Die IGA-Aufgabe.Bei der Musterlösung war die Fläche unabhängig von der Geometrie zu bepflanzen – aber eben nur im Mittel.

Rikes seriöse Lösung der IGA-Aufgabe
Rike hat schon gemerkt, dass ihre zufällige Anordnung von 6 Blumen pro Quadratmeter Charly in der IGA-Aufgabe nicht gefallen hat, ja, dass diese Lösung nicht nur Charly nicht gefällt sondern auch auf der IGA 2017 keinen Beifall gefunden hätte. So überlegt sie, ob es nicht doch eine seriöse Lösung gibt. Sie erinnert sich, dass Gärtner häufig diagonale Anordnungen benutzen. Eine Diagonale ergäbe so ein 5er Muster. Weiterlesen

Die IGA-Aufgabe
Charly bereitet sich an einem Sonntagmorgen auf das nächste Schulhalbjahr vor und schaut sich die letzten Mathe-Abiaufgaben an. Die Analysis-Aufgabe zur Internationalen Gartenbauausstellung 2017 in Berlin hat es ihm besonders angetan.
In dieser Aufgabe soll ein rechteckiges Beet (16 m x 6 m) durch Kurven der Form
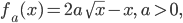
geteilt werden, siehe Abbildung.
Weiterlesen

AI-generierte Bilder III: Variationen
Rike ist nicht ganz glücklich über die DALL.E-Ergebnisse zu ihrem Bild mit Sinus- und Kosinusfunktionen, die ein Orthonormalsystem für 2π-periodische Funktionen bilden. Sie hatte sich gedacht, dass die „Künstliche Intelligenz“ intelligent ist und die speziellen Funktionen erkennt. Sie wird immer wütender je länger sie darüber nachdenkt.

AI-generierte Bilder II: Diffusionsmodell
Nachdem das Erzeugen von fotorealistischen Bildern mit konkreten Vorgaben mittels AI so schief gelaufen ist, hat Rike eine andere Teststrategie. Sie will testen, wie intelligent die „Künstliche Intelligenz“ wirklich ist. So viele intelligente Algorithmen, so viel Mathematik, was versteht die „Künstliche Intelligenz“ wirklich von Mathematik? So gibt sie probeweise ihr „altes“ Bild von einigen Sinus- und Kosinus-Funktionen ein. Diese bilden ein Orthonormalsystem, gerade das hat sie damals Ben erklärt. Die Darstellung von 2π-periodischen, quadratisch integrierbaren Funktionen als Summe von solchen Schwingungen heißt Fourier-Reihe. Das ist ein wichtiges mathematisches Konzept, in Funktionen Schwingungen zu finden und zu benutzen. Es hat viele technische Anwendungen. Rike fragt sich, ob DALL.E diese Schwingungen erkennen und intelligent variieren kann. Weiterlesen

AI-Text-generierte Bilder, I: Semantik
Rike vertreibt sich die Zeit mit dem Testen von DALL.E. Sie hat viel Spaß daran. Ihr Ziel ist es, ein AI-generiertes Bild zur rot-grünen Urnenaufgabe zu erzeugen. Doch in welchen Varianten sie auch „Urne mit 3 roten und 2 grünen Kugeln“ (Urn with 3 red balls and 2 green balls) eingibt, sie erhält kein einziges Bild mit einer Urne, 3 roten und 2 grünen Kugeln. Da kommt Charly von seinem Training herein und fragt, was sie da so macht. Sie erzählt es ihm.

Die rot-grüne Urnenaufgabe
Für Charly sind die Sommerferien zu Ende, er unterrichtet wieder Mathe und trainiert eine Volleyballmannschaft. In diesem Schuljahr soll er sogar das Mathe-Abi betreuen. Doch die Lösung einer Statistikaufgabe aus dem Jahr 2020 versteht er nicht und fragt Rike.
Charly Rike, schau mal hier, diese Statistikaufgabe mit den 3 roten und 2 grünen Kugeln verstehe ich nicht, also die Aufgabe schon, aber nicht die Lösung. Wo kommt denn bei a) die blaue Kugel her? Wieso darf im 3. Zug ebenfalls keine Kugel gezogen werden?
Rike Haha, ist ja witzig! Ändern sich die Kugeln? Ziehen einer Kugel ohne Kugel? Sehr merkwürdig. Weiterlesen

Rikes alternative Bonsai-Aufgabe
Rike und Charly haben Sommerferien. Während Charly im Wald joggt, schaut sich Rike Charlys Sammlung ehemaliger Abi-Aufgaben an. Da findet sie diese Bonsai-Aufgabe:
Die originale Bonsai-Aufgabe
2.2 Analysis: Bonsai-Bäume
Bonsai bezeichnet eine spezielle japanische Gartenkunst, bei der Bäume durch Züchtung in einem Gefäß extra klein gehalten werden. Das Wachstum eines bestimmten Bonsai-Baumes lässt sich bis zum Erreichen der maximalen Höhe für t ≥ 0 mit der Funktion
beschreiben.
Dabei gibt t die Zeit in Jahren und f(t) die Höhe in cm an.
a) Bestimmen Sie die Höhe des Baumes nach 4 Jahren und nach 8 Jahren.
b) Berechnen Sie die maximale Höhe des Baumes. Geben Sie an, wie viele Jahre der Baum wächst.
c) Berechnen Sie die höchste Wachstumsgeschwindigkeit. Es genügt die Bearbeitung mit dem notwendigen Kriterium.
[…]
[Mathematik Abitur 2022, S. 72 ]

Die Gutschein-App
Charly kommt vom Joggen, duscht sich, schaut auf sein Handy und findet unerwünschte Werbung. Rike hört Musik und sortiert den Einkauf in den Kühlschrank.
Charly Habe ich dir eigentlich schon von der schwierigen Stochastik-Abiaufgabe "Gutschein-App" erzählt?
Rike Nö, was ist damit?
Charly Sie hat mehrere Bugs drin, ich hätte ein Problem, die zu korrigieren. Doch das war vor meiner Zeit hier.
Rike So schlimm? Zeig mal her!
Charly Hier!
Die Gutschein-App und Anna
Stochastik: Gutschein-App
In einer Handy-App kann ein Nutzer jeden Tag bis zu 8 Überraschungsboxen öffnen, wobei jede Box eine Wahrscheinlichkeit von 30 % hat, einen Rabattgutschein zu enthalten.
[…]
c) Anna hat bereits zwei Tage in Folge genau 6 Gutscheine erhalten. Sie behauptet, dass sie deshalb eine geringere Wahrscheinlichkeit hat, am nächsten Tag wieder 5 Gutscheine zu bekommen. Beurteilen Sie die Aussage von Anna.
[Mathematik Abitur 2022, S. 13]