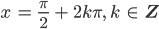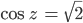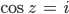Finja ist in Quarantäne, wie die anderen Italienrückkehrer auch. Den offenen Brief hat sie mit Justin und Fabian verfasst, Max hat ihn online gestellt und wichtigen Institutionen zugeschickt. Die Hausaufgaben sind schnell erledigt, ihr ist langweilig. Sie stöbert im Haus und findet auf dem Dachboden ein uraltes Matheschulbuch (1961).
Darin findet sie die Aufgabe
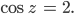
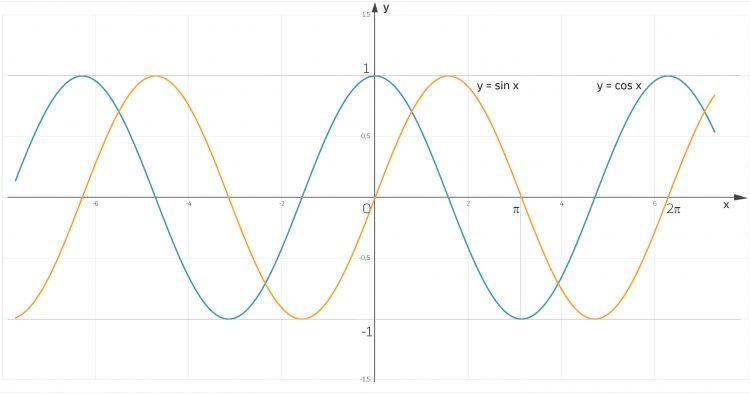
Reelle Sinus- und Kosinus-Funktionen
Finja findet das merkwürdig, denn eigentlich haben die Kosinus- und Sinusfunktionen nur Werte zwischen -1 und 1.
Eulersche Formeln
Doch im Komplexen, mit der eulerschen Formel
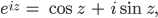
einem Additionstheorem und ein paar Umformungen gelingt die Lösung der Aufgabe. Sie ist sehr überrascht und muss das mit Justin diskutieren. Sie vereinbaren einen Chat.
Justin Hallo Finja, wie geht es Dir?
Finja Hallo Justin, es geht. Höre, Justin, ich habe ein altes Mathebuch auf dem Dachboden gefunden, da steht die Aufgabe
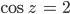
drin.
Justin Das ist ein Witz!
Finja Nö, ist kein Witz!
Justin Und? Gibt’s da eine Lösungsstrategie?
Finja Ja, im Komplexen! Kennst du dich mit komplexen Zahlen aus?
Justin Hmm, lass mal hören.
Finja Zuerst nehmen wir die eulersche Formel:
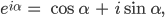
Und gleich noch die für den negativen Winkel:
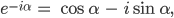
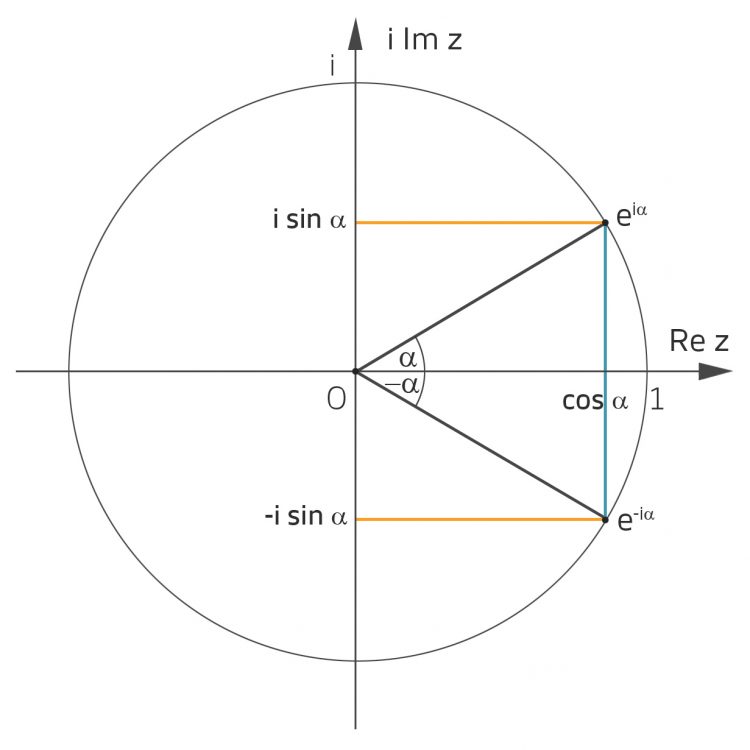
Justin Okay.
Finja Die beiden Gleichungen werden addiert und nach dem Kosinus umgestellt:
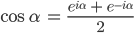
Den Sinus bekommst du durch Subtraktion der beiden Gleichungen:
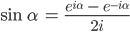
Justin Na gut! Die gute alte Eulerformel. Und weiter.
Additionstheorem
Finja Jetzt nehmen wir das Additionstheorem für den Kosinus:
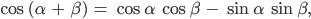
das benutzen wir für komplexe Zahlen:
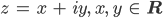
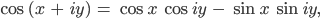
Justin Aha! Dann gehst du davon aus, dass es den Sinus und den Kosinus von komplexen Zahlen gibt und dass dieselben Gesetze gelten?
Finja Ja.
Justin Na!
Finja Dann geht es weiter: Für den Term cos iy nehmen wir die Kosinus-Formel aus den beiden Eulerformeln:
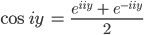
Justin Das kannst du vereinfachen, lass mich mal:
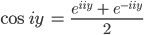
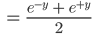
Finja Stimmt! Genauso mit dem Sinus:
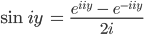
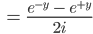
Insgesamt kriegen wir aus dem Additionstheorem und den Umformungen hier:
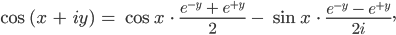
Justin Okay!
Finja Jetzt kommen wir zur eigentlichen Aufgabe:
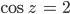
Jetzt ist z komplex und die 2 musst du dir auch komplex denken:

Justin Okay!
2 nichtlineare Gleichungen
Finja Jetzt nehmen wir die lange Formel für Kosinus von x +iy und zerlegen die in Real- und Imaginärteil und kriegen 2 Gleichungen.
Justin Klar! Für den Realteil:
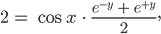
und für den Imaginärteil:
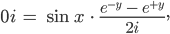
Jetzt musst du das nur noch nach x und y auflösen? Richtig?
Finja Stimmt! Gottseidank steht bei der 2. Gleichung links eine Null. Da haben wir
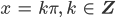
und
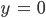
als Lösung. Das setze ich in die Gleichung für den Realteil ein:
Für

kriege ich
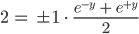
Justin Was ist das mit den beiden Vorzeichen?
Finja Je nachdem, welches k du nimmst. Für k = 0 ist
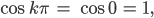
für k = 1 ist
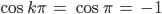
usw.
Justin Aha!
Finja Die Gleichung mit der 2 multipliziere ich mit
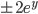
Und erhalte:
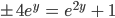
Alles auf eine Seite ergibt:
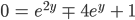
Die beste Idee
Und jetzt kommt die beste Idee: Mit der Substitution
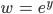
kriegen wir eine quadratische Gleichung:
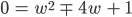
Und die hat die Lösungen:
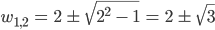
und
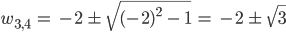
Justin Echt krass!
Finja Danke! Jetzt schauen wir noch, welche Lösungen akzeptabel sind. Wir hatten ja die Substitution
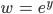
für reelle y. Also ist w positiv. Da fallen die Lösungen w3, 4 weg. Die kamen von den ungeraden k.
Finale Lösungen für cos z = 2
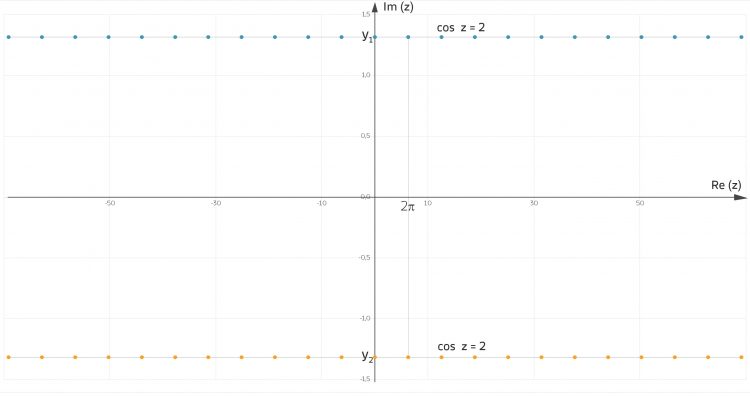
Also habe ich die Lösungen
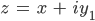
und
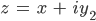
mit
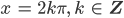
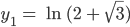
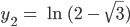
Justin Wow! Zweimal unendlich viele Lösungen! Nicht schlecht! Du hattest doch am Anfang ein Produkt, was Null wird. Was ist mit dem 2. Faktor?
Finja Richtig! Wenn y = 0 ist, wird aus der Gleichung für den Realteil
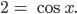
Weil x reell ist, entfällt dieser Fall.
Justin Schön, du hast es vollständig gelöst! Finja, ist dir jetzt immer noch langweilig?
Finja Haha!
***
Übungsaufgaben
Lösungen
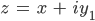
und
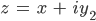
mit
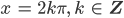
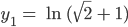
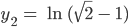
wie 1., nur