Rike ist mit ein paar Freunden bei der großen Erstsemesterparty im Ringlokschuppen in Bielefeld. Natürlich stehen wieder die IT-, CG-, VFX- und Medienleute zusammen. So auch Rike und Ben.
Rike Hey Leute, ich habe ein geometrisches Problem: Wie kann ich parallele Geraden erkennen? Kann mir jemand helfen?
Das Parallelenaxiom
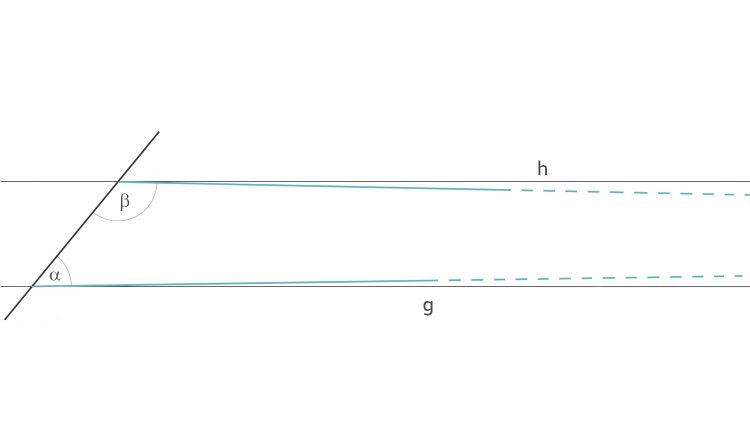
Ben Ach, das Parallelenaxiom von Euklid! Es besagt, dass sich 2 Linien g und h (, die in der Ebene liegen,) schneiden, wenn man sie bis ins Unendliche verlängert sowie 
und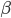 
zusammen kleiner als zwei rechte Winkel sind. Wisst Ihr, man konnte es lange nicht beweisen. Man kann es auch heute nicht beweisen, weil es nur im euklidischen Raum richtig ist, in anderen, nicht euklidischen Räumen gilt es nicht.
Das Parallelenaxiom und Schopenhauer
Da habe ich neulich was entdeckt, nämlich dass Schopenhauer das grundsätzlich anders sieht. Er meint, dass Offensichtliche muss man nicht beweisen. Das sei bei allen geometrischen Problemen so. Wartet mal, ich suche die Stelle eben einmal heraus. Hier:
„Die Eukleidische Demonstriermethode hat aus ihrem eigenen Schooß ihre treffende Parodie und Karikatur geboren, an der berühmten Streitigkeit über die Theorie der P a r a l l e l e n und den sich jedes Jahr wiederholenden Versuchen, das elfte Axiom zu beweisen. Dieses nämlich besagt, und zwar durch das mittelbare Merkmal einer schneidenden dritten Linie, daß zwei sich gegen einander neigende (denn dies eben heißt 'kleiner als zwei rechte seyn'), wenn genugsam verlängert, zusammentreffen müssen; welche Wahrheit nun zu kompliziert seyn soll, um für selbstevident zu gelten, daher sie eines Beweises bedarf, der nun aber nicht aufzubringen ist, eben weil es nichts Unmittelbares giebt. Mich erinnert dieser Gewissensskrupel an die Schillersche Rechtsfrage:
'Jahre lang schon bedien' ich mich meiner Nase zum Riechen:
Hab' ich denn wirklich an sie auch ein erweisliches Recht?'
ja mir scheint, daß die logische Methode sich hiedurch bis zur Niaiserie steigere. Aber gerade durch die Streitigkeiten darüber, nebst den vergeblichen Versuchen, das u n m i t t e l b a r Gewisse als bloß m i t t e l b a r gewiß darzustellen, tritt die Selbständigkeit und Klarheit der intuitiven Evidenz mit der Nutzlosigkeit und Schwierigkeit der logischen Ueberführung in einen Kontrast, der nicht weniger belehrend als belustigend ist. Man will hier nämlich die unmittelbare Gewißheit deshalb nicht gelten lassen, weil sie keine bloß logische, aus dem Begriffe folgende, also allein auf dem Verhältnis des Prädikats zum Subjekt, nach dem Satze vom Widerspruch, beruhende ist. Nun ist aber jenes Axiom ein synthetischer Satz a priori und hat als solcher die Gewährleistung der reinen, nicht empirischen Anschauung, die eben so unmittelbar und sicher ist, wie der Satz vom Widerspruch selbst, von welchem alle Beweise ihre Gewißheit erst zur Lehn haben. Im Grunde gilt dies von jedem geometrischen Theorem, und es ist willkürlich, wo man hier die Gränze zwischen dem unmittelbar Gewissen und dem erst zu Beweisenden ziehn will.“
Rike Hahaha.
Geometrie als Vorübung für Philosophie
Ben Schopenhauer schreibt weiter und bezieht sich auf Plato:
"... dass er [Plato] die Geometrie als Vorübung betrachtete, durch welche der Geist der Schüler sich an die Beschäftigung mit unkörperlichen Gegenständen gewöhnte, nachdem derselbe bis dahin, im praktischen Leben, es nur mit körperlichen Dingen zu thun gehabt hatte (Schol. in Aristot. p. p. 12, 15.)."
Und das könne man nicht verallgemeinern. Es kommt noch schlimmer. Am Ende seines mathematischen Kapitels in Die Welt als Wille und Vorstellung schreibt er:
“... Der einzige unmittelbare Nutzen, welcher der Mathematik gelassen wird, ist, daß sie unstäte und flatterhafte Köpfe gewöhnen kann, ihre Aufmerksamkeit zu fixieren.“
Alle lachen.