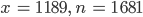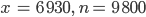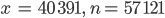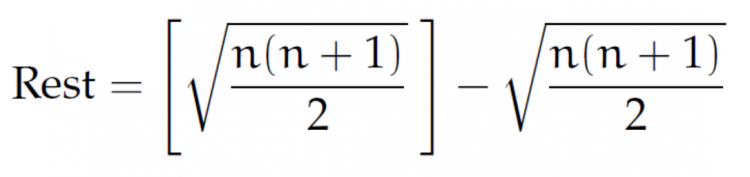Max ist mit seinem kleinen Team gut in der Region Westbengalen, nördlich von Kalkutta (Indien) angekommen. Das Team soll den Bau einer Schule dokumentieren. Im Oktober ist das Wetter recht angenehm, man kann abends lange draußen sein. Max und seine Lemgoer Freunde verabreden sich mit ein paar jungen einheimischen Lehrern unter dem schönsten indischen Sternenhimmel. Einer von ihnen, Dipankar, erzählt von seinem mathematischen Vorbild, dem indischen Mathematiker Srinivasa Ramanujan (1887-1920). Er war sehr begabt und hat viele Eigenschaften von Zahlen untersucht. Es gibt eine kleine Anekdote von Ramanujan:
Ein Freund kam zu ihm zum Mittagessen und erzählte von einer Denksportaufgabe: In einer Straße sollen die Häuser mit den Nummern 1 bis n linear geordnet stehen. Das Haus mit der Nummer x soll das sein, wo die Summe der Hausnummern links von ihm gleich der Summe der Hausnummern rechts von ihm sind. Sein Freund hat die Lösung durch Probieren gefunden, doch Ramanujan hat noch mehr Lösungen durch Nachdenken gefunden.
Max überlegt nun auch. Er kennt ja noch die gaußsche Summenformel für die ersten n Zahlen. Schließlich findet er einen Zusammenhang für n und x:
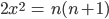
Max' Ansatz
Jetzt überprüft er, ob
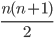
eine Quadratzahl ist. Er zieht die Wurzel daraus und zieht das vom ganzen Anteil (, die Gauß-Klammer [.]) ab. Was übrig bleibt, nennt er Rest.
Mit einer App erhält er ein schönes Muster und muss nur noch prüfen, ob der Rest gleich 0 ist.
Kleine Lösungen
So findet er numerisch die ersten Lösungen
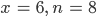
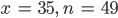
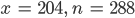
Dipankar und seine Freunde klatschen. Max hat den Ramanujan-Test bestanden.
***
Übungsaufgabe
Finde weitere Lösungen  und
und  .
.
Lösungen