Wie man aus Bildern 3D-Daten rekonstruieren kann

Ben hat Rike zu seiner Firma eingeladen. Er ist ihr schuldig, ihr Parallelenproblem zu erklären.

Rikes Frage war, ob man aus einem Foto von 2 Geraden geometrische Eigenschaften herleiten kann.

Rikes Parallelenproblem

Rike Ben, sag, sind die beiden Gerade parallel?

Ben Oh, mal langsam, Rike. Du fragst Fragen, die aktuelle Forschungsthemen berühren. Wenn man aus einem Kamerabild alle Infos kriegt, dann hätten wir schon längst sichere selbstfahrende Autos! Du fragst nach der Rekonstruktion von 3D-Daten aus 2D-Abbildungen. Da hat man echt viele Sachen zu beachten – auch die Kamera selbst.

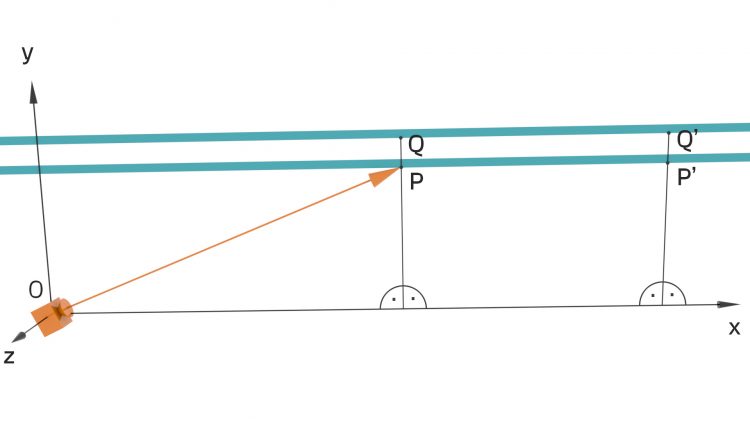
Rike Klar, ich weiß. Was kann man denn tun? Ich will ja nur wissen, ob die beiden Geraden den gleichen Abstand haben. Schau mal, hier habe ich die Punkte P und Q auf den Geraden und ein Stück weiter P‘ und Q‘. Ich will wissen, ob der Abstand PQ gleich dem Abstand P’Q‘ ist.

Bens Setting

Ben Okay, verstehe. Wenn ich Dir zeige, wie man die Koordinaten eines Punktes, sagen wir mal P, berechnet, dann kannst Du auch alle anderen Punkte berechnen.

Rike Ja, das kriege ich hin.

Ben Dann lass uns ein Koordinatensystem einrichten und eine Kamera doch mal in den Nullpunkt legen. Das bedeutet, dass wir den Standort der Kamera genau kennen.

Rike Klar, die legen wir in den Nullpunkt.

Ben Weiter, die Kamera muss nicht nur fotografieren können, sondern auch den Abstand zu P messen können, optisch zum Beispiel oder wie auch immer. Sagen wir mal, der Abstand 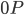ist 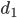und bekannt. Aus diesem ersten Kamerabild kann man nicht die absoluten Koordinate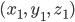n von 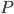berechnen.

Rike Okay, ist ja nur eine Projektion, eine Information der 3. Dimension geht dabei verloren. Den Standpunkt der Kamera kann man aus dem Bild nicht ermitteln.

Ben Stimmt, dann lass uns ein zweites Bild mit der Kamera von Standort K₂ machen. Den Standort K₂ lege ich mal auf die x-Achse. Ich habe das Koordinatensystem so gelegt, dass die beiden Kamerastandpunkte und P in der x-y-Ebene liegen.

Rike Hey, das war clever, aber das ist ja eigentlich klar, 3 Punkte liegen immer in einer Ebene.

Ben Gut. Dann brauchen wir den Abstand der zweiten Kamera zu P, das soll 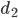sein. Außerdem muss der Abstand der beiden Kamerapositionen 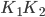bekannt sein, das soll 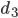sein.

Herleitung der Gleichungen für die 3D-Rekonstruktion

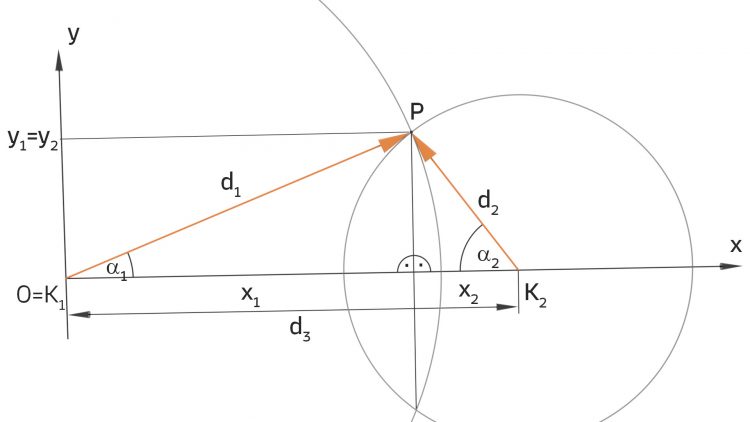
Hier im Bild siehst Du die Koordinaten des Punktes P

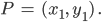
Er liegt jetzt in der Ebene, wir können

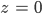
setzen.

Rike Okay. Jetzt sehe ich es auch, wir haben zwei rechtwinklige Dreiecke. Für die Höhe 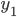von P, die gleich der Höhe 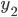ist, können wir die Beziehungen

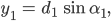
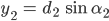
aufschreiben und die gleich setzen:

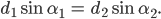
Ja, warte mal, für die x-Werte kann ich das auch aufschreiben:

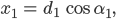
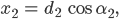
nur das bringt nicht viel. Aber Du hast mir ja erklärt, dass der Abstand 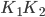bekannt ist, das habe ich noch nicht genutzt! Hm, ja, hm,

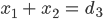
Ben Hey, Rike, hast Du Dich schon mal damit beschäftigt? Ist ja super, lass uns Deine Gleichungen etwas anders aufschreiben:

Finale Gleichungen

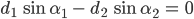
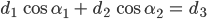
Rike Super, ein Gleichungssystem für die Winkel 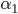und 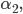nicht schlecht. Leider nichtlinear! Der alte Gauß hilft Dir da nicht weiter!

Ben Nein, aber Du siehst im Bild, wenn ich um die Kamerastandpunkte K₁ und K₂ Kreise mit den Radien 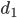und 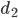 zeichne, wenn außerdem die Dreiecksungleichung

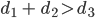
erfüllt ist, dann finde ich genau den Schnittpunkt P und einen dazu gespiegelten. Das heißt, es gibt unter der Voraussetzung der Dreiecksungleichung genau eine sinnvolle Lösung P.

Fazit

Rike Okay, das habe ich auch erwartet, das ist kein Wunder. Du meinst also, dass man mit 2 Kameras, die die Abstände 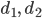 und 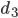messen und die die Bedingung

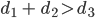
erfüllen, stets die Winkel 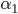und 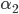und daraus die Koordinaten des Punktes P bestimmen kann?

Ben Richtig. Soll ich Dir jetzt noch die Formel für 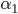und 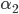herleiten? Das ist ja reine Mathematik, aber wenn Du willst...

Rike Ach, Ben, danke, das hat doch schon jede Firma mit ein paar Informatikern hergeleitet. Jede Computertomographie, jedes GPS-, jedes Motion Capture System, jede Lichtfeldkamera, natürlich auch Google und Gott weiß, wer noch, benutzen das heutzutage, ist okay.

Ben Na, ich bin auch Informatiker!

Rike Ben, war nicht bös' gemeint. Schau mal, jetzt habe ich 300 Mal diese Geraden fotografiert, ich habe so eine richtige Computertomografie gemacht, Du sagst, 2 hätten gereicht, aber gefallen sie Dir nicht ein bisschen?

Ben Schon krass!

Übungsaufgabe

Was passiert, wenn die Entfernungen 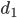und 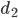mit einer Ungenauigkeit von 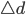gemesssen werden und außerdem die Kamerastandpunkte eng beieinander sind, so dass der Abstand 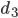in der Größenordnung von 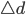ist?