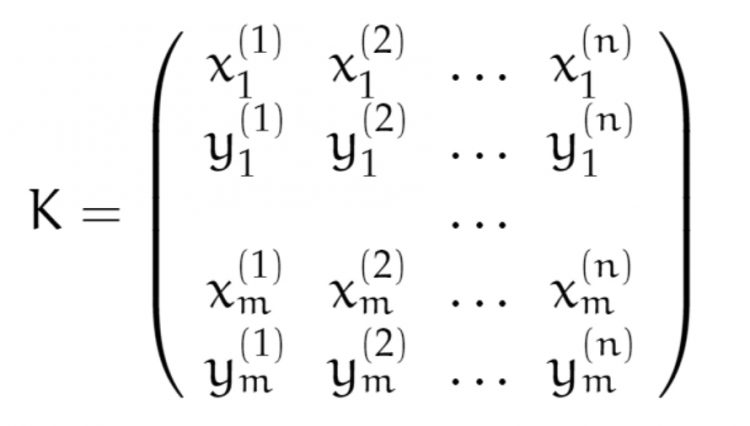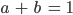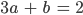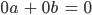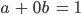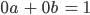Ben und Rike treffen sich wieder, Rike will heute endlich wissen, womit er sich beschäftigt.
Ben Weißt Du, ich soll duch lineare Überlagerung von Gesichtern aus einer Bibliothek ein gegebenes Gesicht erstellen, und zwar möglichst schnell – in Echtzeit. Nehmen wir mal die bekannte Kachujin.
Die soll mal exemplarisch aus Maria und Stefanie entstehen.
Kachujin, Maria und Stefanie
Rike Sag mal, bist Du verrückt? Die sind doch so verschieden, das geht doch niemals!
Ben Nee, wir haben natürlich nicht nur die beiden Models, sondern viel mehr.
Rike Und wie geht Ihr vor?
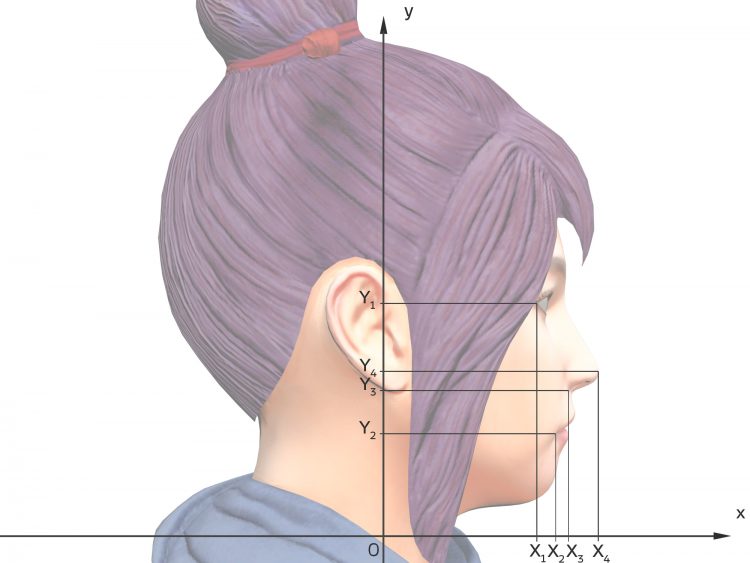
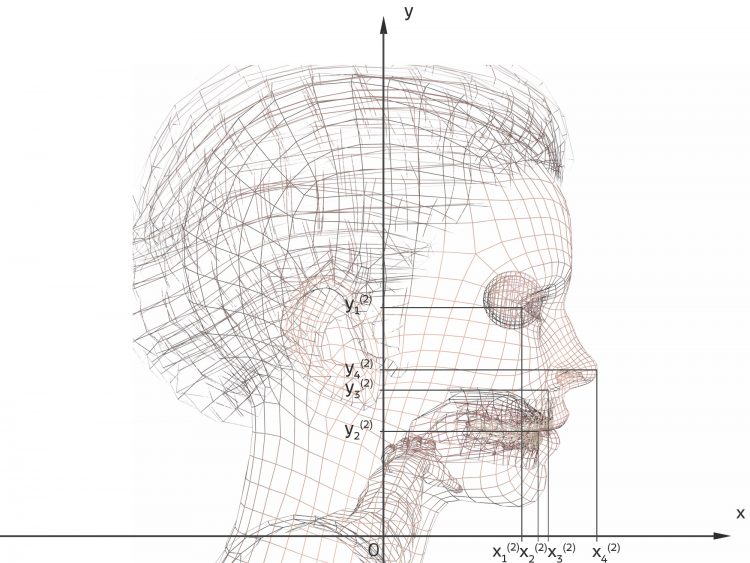
Ben Wir bilden einen linearen Vektorraum, wir überlagern die Mädels linear. Aber zuerst stellen wir ein geeignetes Koordinatensystem auf und notieren die Koordinaten von markanten Punkten im Gesicht.
x-, y-Koordinatensysteme
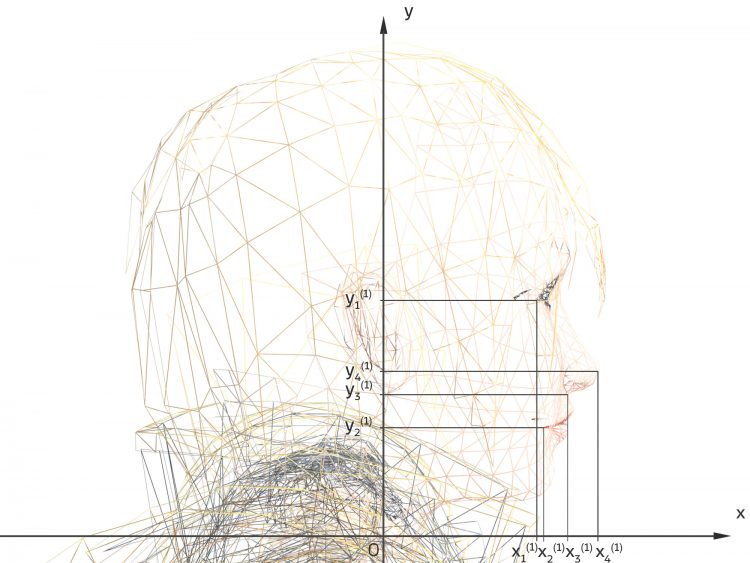
Lineares Gleichungssystem
Zum Beispiel, wenn Du die Lage des rechten äußeren Augenwinkels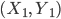 
für Kachujin bestimmen willst, geht das so:
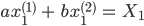
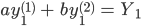
Rike Verstehe, Ihr nehmt a-Mal Maria und b-Mal Stefanie, um Kachujin zu berechnen, ein lineares Gleichungssystem für den Augenwinkel. 2 Gleichungen für 2 Unbekannte, a und b. Mit ein bisschen Glück, wenn die Koeffizientenmatrix für n Charaktere und m Merkmale
regulär ist, kannst Du das lösen.
Ben Genau. Tatsächlich wollen wir eine umfangreiche Bibliothek aufstellen, die Saarbrückener nehmen ca. 200 Gesichter, das wären also 200 Unbekannte. Wir stellen erst mal ein paar Gleichungen auf. Gewöhnlich nimmt man die Nasenspitze, den Mundwinkel usw. In der Zeichung sind 4 Punkte ausgezeichnet, die ergeben für die x- und y-Koordinaten jeweils 4 Gleichungen, also 8 Gleichungen.
Probleme
Rike 8 Gleichungen für 200 Unbekannte?
Ben Ja, wenn eine quadratische Untermatrix der Koeffizientenmatrix K regulär ist, dann können wir 8 Veränderliche bestimmen und 192 bleiben frei wählbar. Diese 192 bilden einen linearen Unterraum. Mein Job ist es, aus diesen vielen Lösungen eine geeignete auszuwählen und möglichst schnell zu berechnen. Wenn ich immer die ersten 8 Charaktere fest nehme, sehen sich die überlagerten Gesichter recht ähnlich.
Rike Aber sag mal, sind denn 8 Gleichungen nicht ein bisschen wenig? Du überlegst, wie Du die freien Parameter bestimmst, aber willst Du denn nicht 200 Gleichungen aufstellen, 100 Merkmale festlegen?
Ben Naja, das gibt ein ziemlich großes Gleichungssystem. Es soll ja sogar in Echzeit gelöst werden.
Rike Ich find's besser, sorgfältig mit Charakteren umzugehen als schnell was auszurechnen.
Ben Wir arbeiten ja noch dran. Es ist schon mit den 8 Veränderlichen kompliziert genug. Ich habe Situationen, wo das lineare Gleichungssystem nicht lösbar ist.
Rike Das kann ich mir vorstellen! Dann muß Du den unpassenden Charakter aus Deinem System rausnehmen.
Ben Haha.
Übungsaufgaben
Was passiert, wenn die beiden Gleichungen die Gestalt haben:
Lösungen
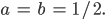Kachujin ist die Überlagerung von Maria und Stefanie, je zur Hälfte.
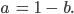Kachujin kann nur Maria sein, Kachujin könnte nur Stefanie sein oder auch die Überlagerung aus beiden, je zur Hälfte... Es gibt unendlich viele Lösungen.- Das Gleichungssstem ist nicht lösbar. Ersetze Stefanie durch jemand anderes.