Als Ben einen interessanten Artikel über zufällige Oberflächenstrukturen im Quanta Magazine gelesen hat, überdenkt er diese zufällige Kachelungsgeschichte, reißt kurzerhand seine (und Rikes) Küchenecke ab und macht alles neu. Ihm ist nämlich aufgefallen, dass Rike die Kacheln mit zufälliger Drehung gleichmäßig angeordnet hat: möglichst in jeder Zeile und Spalte je eine aus den verschiedenen Intervallen. So liegen nun die Kacheln mit den größten Drehungen weit auseinander und die meisten mit den fast unscheinbaren Drehungen bilden das "Mittelfeld". Was passiert aber, wenn er die Kacheln mit noch breiterer Varianz als von Rike vorgeschlagen von innen nach außen wieder mit der Gaußverteilung anordnet? Die Gaußverteilung also doppelt anwendet – auf den Winkel und auf die örtliche Verteilung. Die größten Drehungen kommen zuerst in die Mitte; dann „docken sich“ die anderen mit absteigenden Drehwinkeln an, genau wie im Quanta Magazine, wo sich die Bausteine zufällig andocken und konsistente Strukturen entstehen.
Gaußverteilung mit breiterer Varianz
Ben Diese Gaußverteilung mit einer breiteren Varianz kriege ich doch auch ausgerechnet! Nehmen wir mal
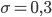
Dann sieht die Wahrscheinlichkeitsdichte der mit
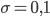
sehr ähnlich.
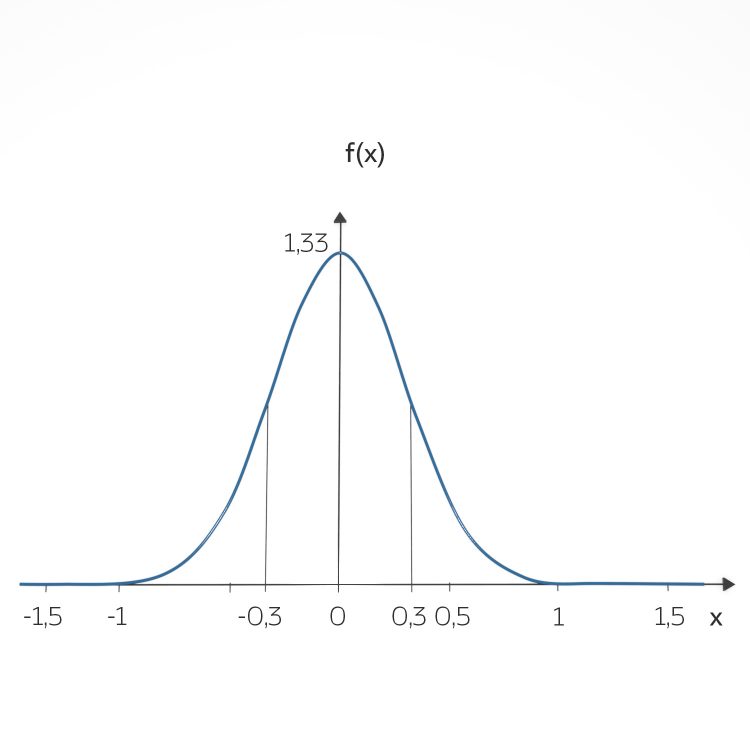
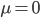und einer größeren Varianz von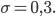 
Für die Wahrscheinlichkeiten muss ich diese Kurve numerisch integrieren, ha, das lernen ja schon die Kinder in der Schule, das kann ich auch:
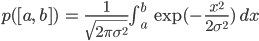
| Drehung um den Winkel in ° | Drehung um den Winkel im Bogenmaß | Anzahl der Kacheln von 100 |
| 0 – 10 | 0 – 0,17 | 22 |
| 10 – 20 | 0,17 – 0,35 | 15 |
| 20 – 30 | 0,35 – 0,52 | 8 |
| 30 – 40 | 0,52 – 0,70 | 3 |
| 40 – 50 | 0,70 – 0,87 | 1 |
| 50 – 60 | 0,87 – 1,05 | 0,5 |
Konstruktion der Kacheln mit doppeltem Zufall
Die negativen Winkel brauche ich nicht zu integrieren, die Funktion ist ja symmetrisch! Okay! Ich nehme ein Raster von 30 x 20 Kacheln. Das sind 600 insgesamt. Dann fange ich mal mit 3 Kacheln an, die drehe ich um ca. 55° und 3 Kacheln, die drehe ich um 55° in die andere Richtung. Die bilden das Zentrum und werden aneinander gesetzt. Und so weiter! Aber immer gleichmäßig von innen nach außen. Hey, das ergibt eine tolle Struktur!
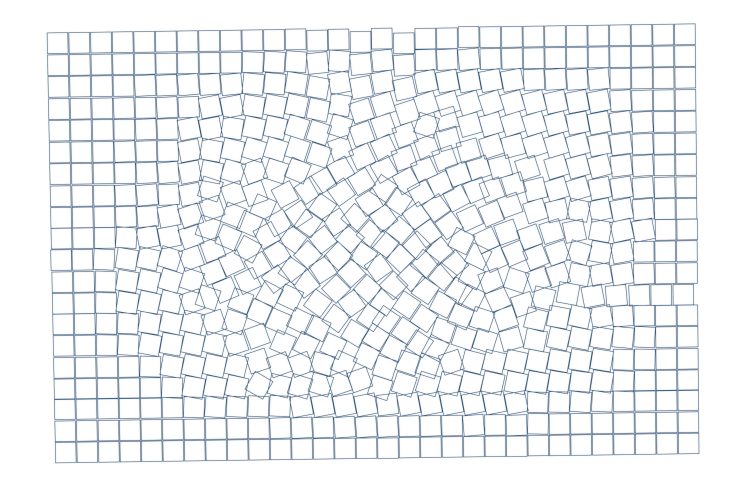
Das muß ich gleich 'mal Kevin Hartnett schicken, das wird ihm gefallen!
Rike O mein Gott, Ben, was hast Du denn gemacht?
Ben Ich habe den doppelten Zufall studiert.
Rike Haha!
Ben Gefällt's Dir etwa nicht?
Rike Nö!
Übungsaufgabe
Konstruiere die Kachelung für den Fall, dass die Drehungen von außen nach innen sortiert werden!