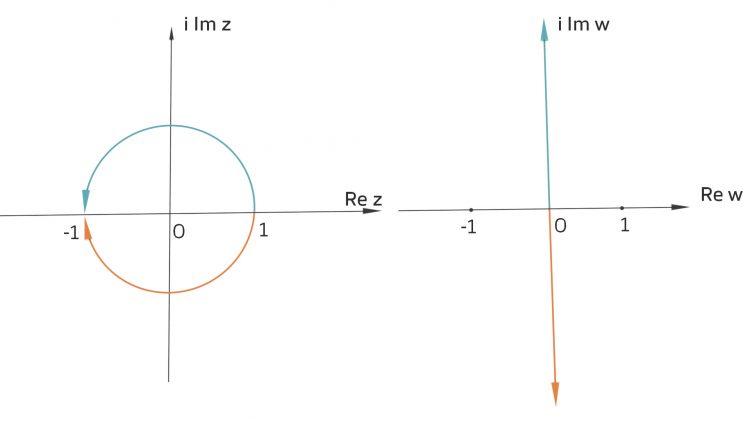Rike geht zu ihrem Nachbarn Ufuk, ein kaputtes Notebook unter dem Arm.
Rike Hi, Ufuk, ich glaube, ich habe eben mein Läppi zerschossen. Ich wollte mal mit der Mikrowelle testen, ob ich unser WLAN-Netz erweitern kann. Ich habe ein Loch in das Gerät gebohrt und ein Antennenkabel mit Antenne reingesteckt. Dann hat es geknallt und mein Laptop hat seinen Geist aufgegeben. Blöde Sache.
Ufuk (atemlos) Was hast Du gemacht, ich fasse es nicht!! Noch nie was von Anpassung gehört? Das Magnetron muss doch mit seinem konjugiert-komplexen Ausgangswiderstand abgeschlossen werden, da musst Du einfach ein Anpassungsnetzwerk zwischenschalten, indem Du im Smith-Diagramm guckst, wie Du von Deiner Antenne mit Kabel, die in der Mitte des Diagramms liegt und ...
Rike Stop mal! Was sagst Du, ich soll ein Smith-Diagramm nehmen? Was ist das?
Konforme Abbildung
Ufuk Kennst Du das nicht? Ne‘ konforme Abbildung!
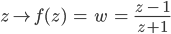
ziemlich coole Sache!
Rike Stopp, das ich mir erst mal genauer anschauen, gib mir eine Chance, Dich zu verstehen!
Ufuk Klar! Hier!
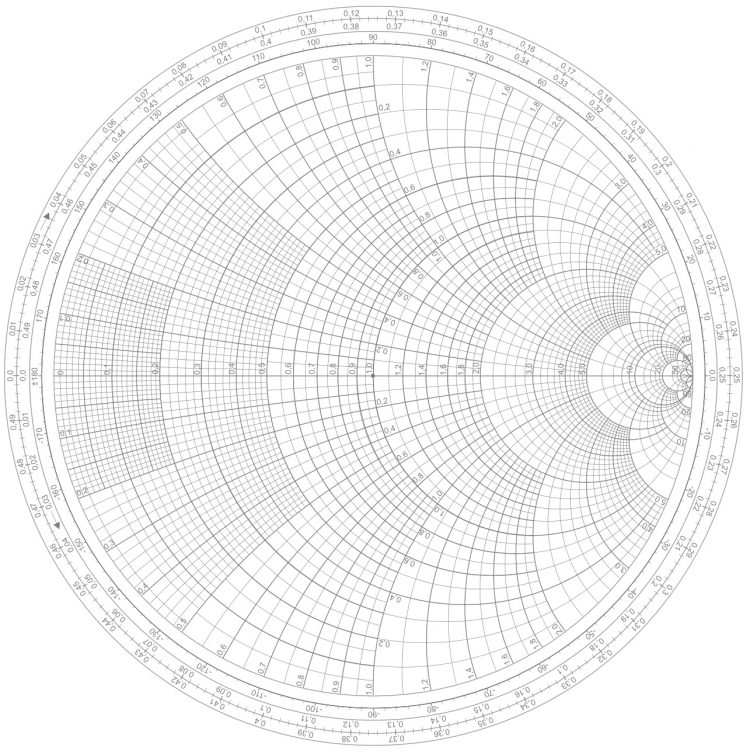
Rike Die Einsen sind ja komisch. Ist das geeicht?
Ufuk Richtig! Wir rechnen mit komplexen Widerständen, Spulen und Kondensatoren! Alle liegen in 
. Aber, wie Du schon erkannt hast, haben wir uns auf eine Referenz geeinigt, vorm Smith-Diagramm steht eine Skalierung. Und zwar nehmen wir Techniker
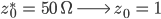
Rike Gut. Dann ist
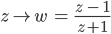
eine Möbiustransformation mit reellen Koeffizienten. Ganz offensichtlich bildet sie reelle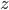 
in reelle 
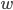ab,
und bei
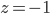
haben wir eine Polstelle.
Der Einheitskreis wird auf die imaginäre Achse abgebildet.
Deine Transformation bildet sogar die obere Halbebene von auf die obere Halbebene an. Und natürlich werden Kreise und Geraden, also verallgemeinerte Kreise wieder in verallgemeinerte Kreise abgebildet.
UfukKann ich jetzt weiter?
Rike Na los!
Herleitung der Schaltung im Komplexen
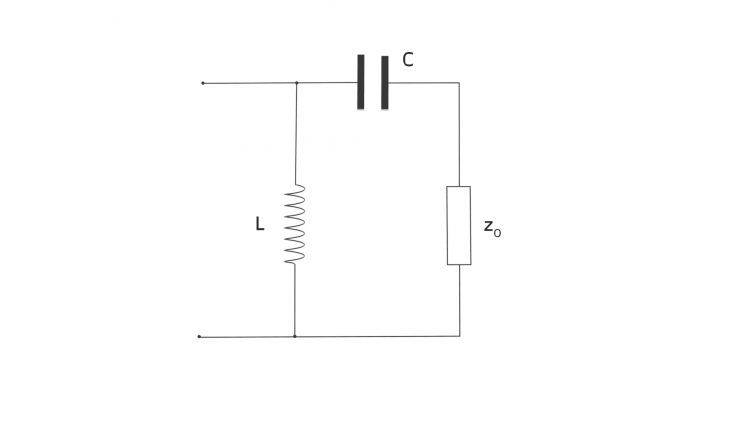
Ufuk Wir fangen mit dem Eingangswiderstand
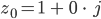
an. Den zeichnen wir ins Diagramm. Das ist unsere Referenz und gleichzeitig der Widerstand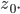 
Für Deine Mikrowelle mit einem Magnetron müssen wir ein geeignetes Anpass-Netzwerk finden, das die Antenne an das Magnetron leistungsmäßig anpasst. Das Magnetron liegt beim Punkt 
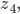da wollen wir hin. Das ist für solche Aufgaben gerade gemacht.
Rike Okay.
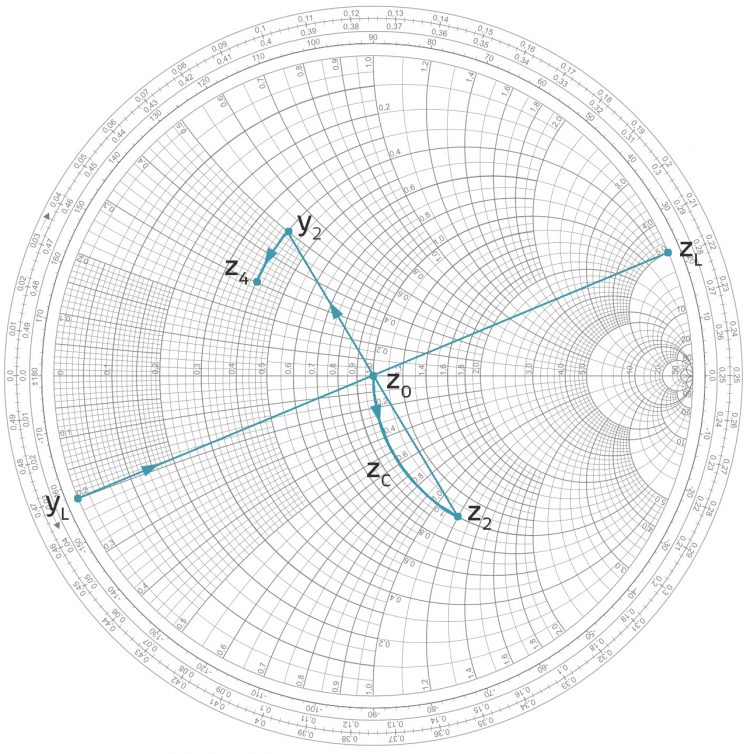
Ufuk Der komplexe Widerstand besteht natürlich aus physikalischen Widerständen, Kondensatoren und Spulen. Zuerst schalten wir einen Kondensator in Reihe dazu. Dazu gehen wir auf der Kurve von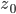 
aus, sagen wir mal um
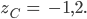
Dann haben wir
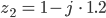
Rike Okay.
Ufuk Jetzt spiegelst Du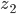 
an 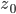und kriegst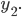 
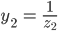
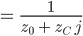
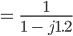
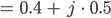
Das ist der Leitwert des Kondensators und des Widerstandes in Reihe geschaltet.
Rike Na gut!
Ufuk Jetzt kommt die Spule! Die wird parallel dazu geschaltet, kriegt auch einen Leitwert. Wir addieren wieder
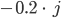
und das ergibt
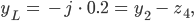
also
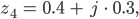
und schon sind wir im Zielpunkt!
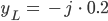
ist der Leitwert der Spule. Durch Spiegelung vo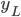n 
an 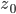kriegen wir
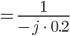
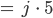
Ich bin fast fertig!
Rike Echt?
Skalierung der physikalischen Größen
Ufuk Jetzt müssen wir nur die nicht genormten Größen berechnen!
Die Widerstände:
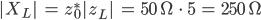
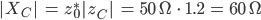
Die Induktivität können wir jetzt mit allgemeinen Formeln für die Bauteile berechnen:
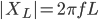
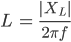
Nehmen wir mal
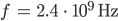
für Deine Mikrowelle?
Rike Gut.
Ufuk Dann kriegen wir eine Induktivität von
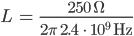
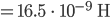
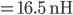
Und für die Kapazität haben wir
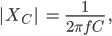
also
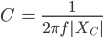
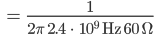
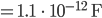
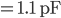
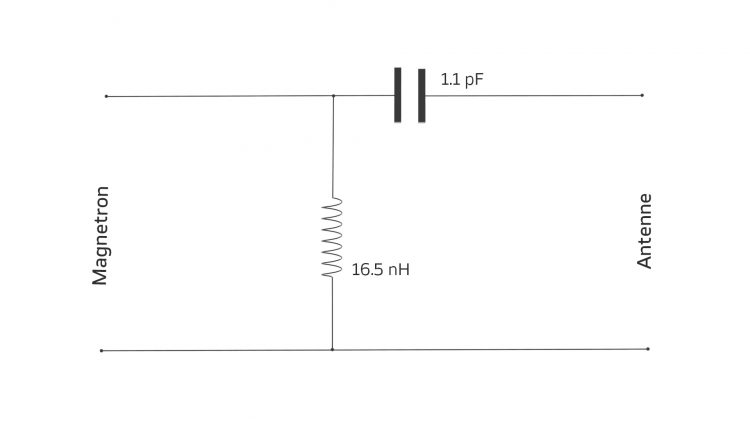
Final
So müsste das klappen! Hier die fertige Schaltung zwischen Magnetron und Deiner Antenne:
Rike Okay, bist Du Dir sicher, dass das passt?
Ufuk Klaro!
Rike Danke, dann probier‘ ich’s mal!
***
Übungsaufgabe
Prüfe, dass der Einheitskreis in die imaginäre Achse transformiert wird.
Lösung
Es ist
