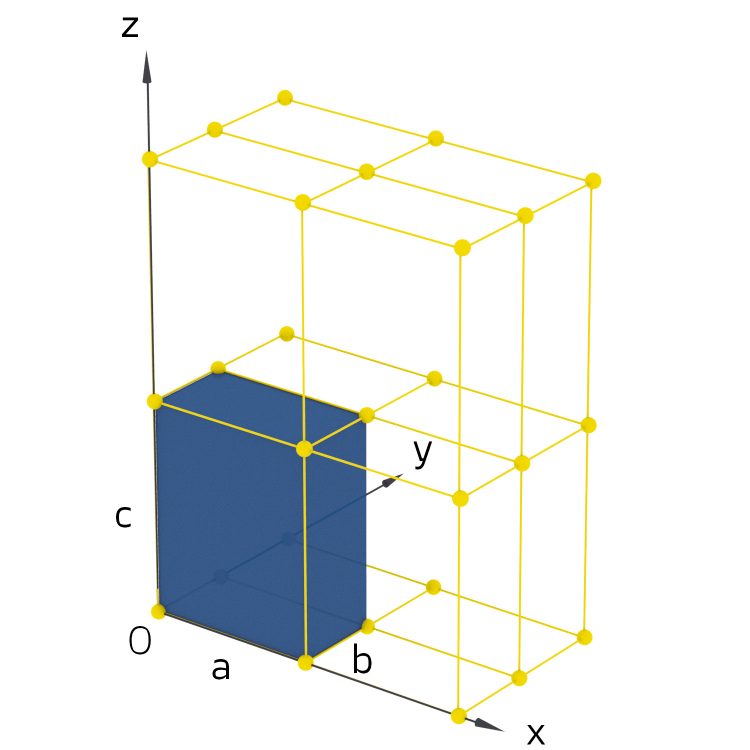
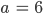Lila ist in Kalkutta und freut sich über Max‘ Nachrichten. Diese Billard-Geschichte hat ihr gut gefallen. Natürlich ist sie stolz auf ihren Landsmann Akshay Venkatesh. Sie möchte seine Arbeiten auch verstehen. Sie liest seine populäre Abhandlung darüber, wie Kristallgitter und Polynomgleichungen zusammenhängen. So schreibt er, dass ein Gitter durch 3 verschiedene Abstände (a, b, c) beschrieben werden kann.
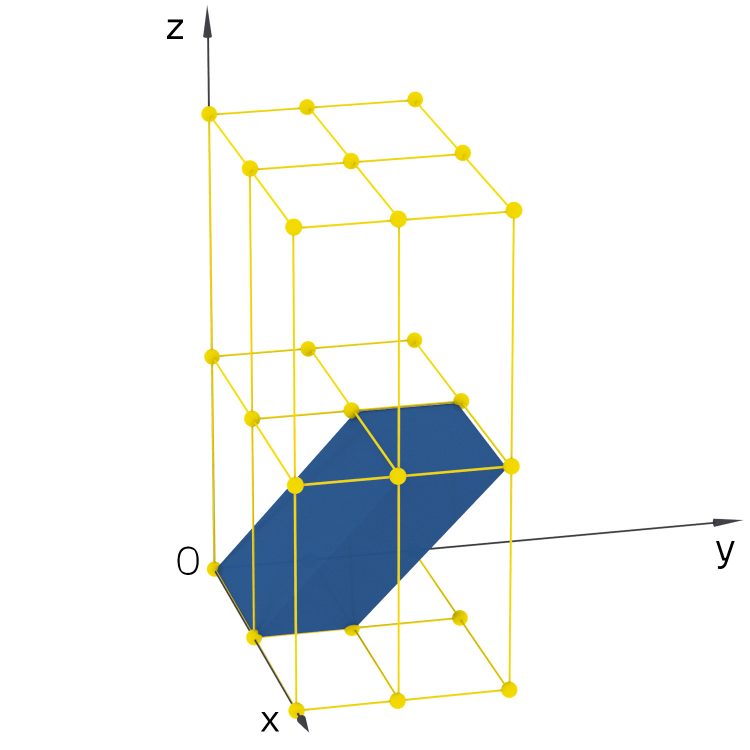
Darin kann man aber verschiedene "Zellen" konstruieren, wie hier die beiden. Die erste Zelle hat 3 rechte Winkel, die zweite nicht.
Wenn man also eine solche Struktur beschreiben will, braucht man 6 Parameter. Und landet so im 6-parametrigen Raum. Die Zellen werden übereinandergestapelt und geben einen speziellen Raum, einen lokal-symmetrischen. Will man Abbildungen zwischen solchen Zellen untersuchen, dann hat man Transformationen dieser 6-dimensionalen Räume. Will man einen Weg, eine Transformation von einer Zelle in eine andere beschreiben, eine Deformation der Zellen, dann muss man eine Gleichung aufstellen, vielleicht eine solche diophantische:
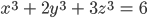
Nun arbeitet Akshay Venkatesh daran, den Zusammenhang von solchen Gleichungen und Gittern aufzustellen und insbesondere Lösungen für die Gleichungen, deren Eigenschaften und ihre Anzahl zu suchen.
Wenn nun die Variablen x, y, z ganz sind, kann die Gleichung unendlich viele Lösungen haben. Betrachtet man aber nicht alle Zahlen x, y, oder z selbst, sondern nimmt man nur die letzten Ziffern in Betracht, so gibt es nur endlich viele Kombinationen. Genau 100, sagt Akshay Venkatesh. Das findet sie irgendwie magisch. Sie möchte das überprüfen. Aber wie?
Beim Tauchen findet sie endlich die Lösung. Sie muss mit Restklassen zur Basis 10 rechnen!
Rechnen mit Restklassen
Sei also
Darin wird modulo 10 addiert. Wenn 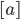 die Restklasse einer Zahl a modulo 10 ist, ist das dann die letzte Ziffer. Man schreibt dafür dann
die Restklasse einer Zahl a modulo 10 ist, ist das dann die letzte Ziffer. Man schreibt dafür dann
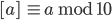
Dafür gibt es auch eine Anweisung (REST) im Tabellenkalkulationsprogramm.
Nun kann sie eine Addition und Multiplikation in 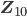 erklären:
erklären:
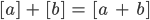
Die Summe zweier "Reste" ist die der Rest der Summe bei der Division durch 10. Und ebenso die Mulitiplikation:
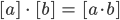
Wenn sie jetzt alle Möglichkeiten für
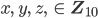
durchgehen will, hat sie sich überlegt, dass sie eine Zahl
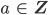
bildet, die aus den Ziffern x, y und z besteht:
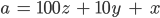
Zusammenhang 
So kann sie a aus dem Tripel (x, y, z) berechnen. Umgekehrt kann sie x, y, z aus a bestimmen, nämlich zuerst die letzte Ziffer x, das ist der Rest von a bei der Division durch 10,
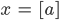
oder
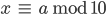
Für y – das ist die Zehnerstelle von a – berechnet sie zuerst die zehnfache Zehnerstelle
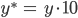
mittels
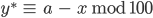
und daraus
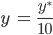
Genauso geht es mit der Hunderterstelle z, sie berechnet
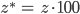
durch
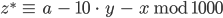
und schließlich
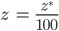
Numerische Lösung
So, das hat sie schon mal geschafft. Jetzt geht sie alle Zahlen a von 0 bis 999 durch, dann hat sie alle Werte von
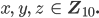
Damit prüft sie
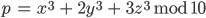
Ist
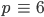 ,
,
hat sie eine Lösung gefunden. Das schafft Lila sehr schnell. das kann jedes Tabellenkalkulationsprogramm lösen. Tatsächlich, sie kriegt 100 Lösungen.
Eigenschaften der Lösungen
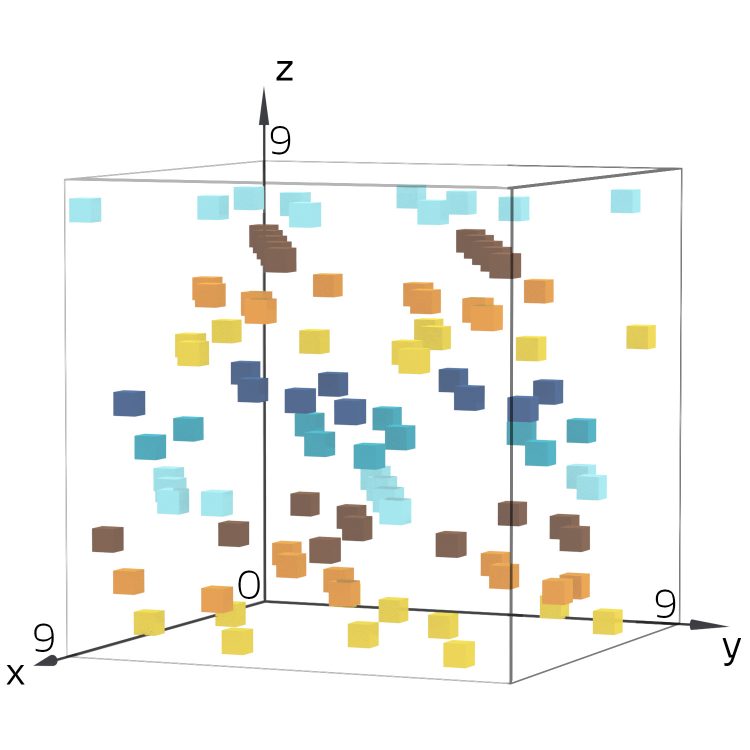
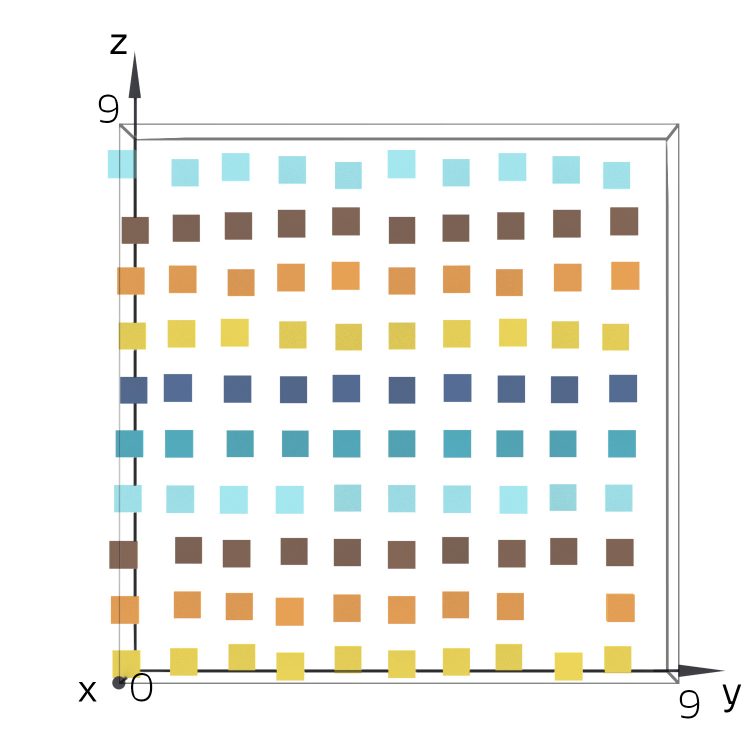
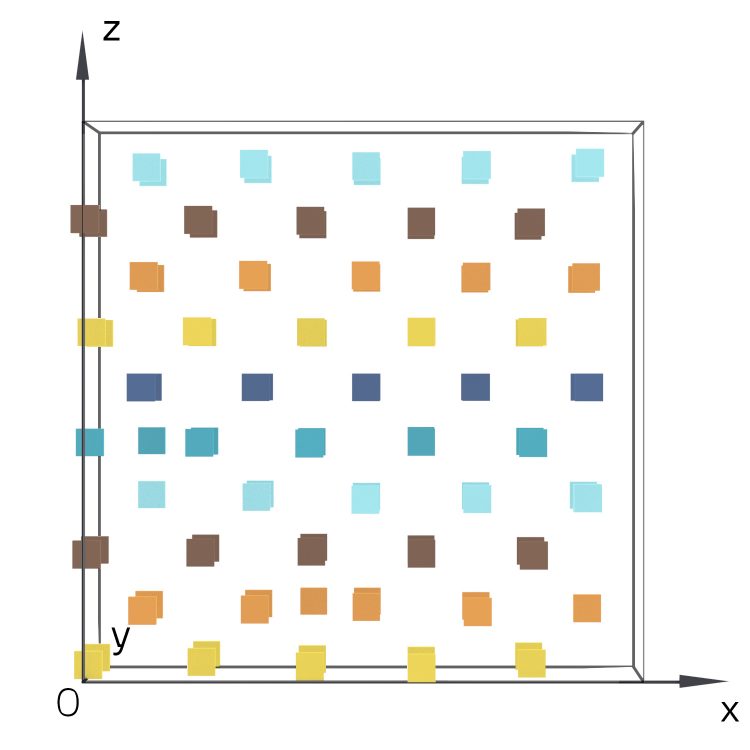
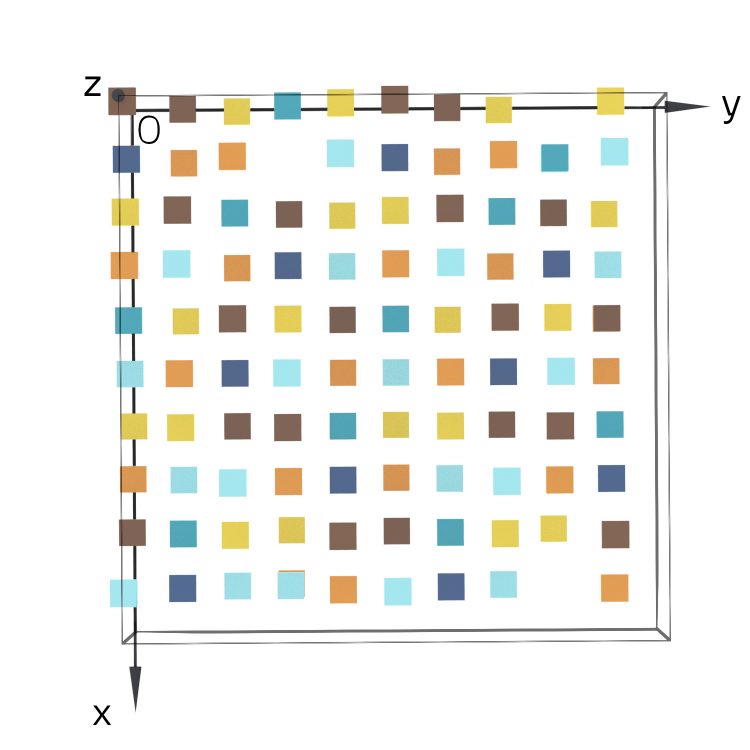
Aber warum sind alle so gleichmäßig verteilt?
Sie zeichnet sie nochmal 3-dimensional und ist verblüfft. Auch hier scheinen die Tripel gleichmäßig in jede Richtung verteilt zu sein.
Das muss sie gleich Max berichten. Ob sie wohl Mathe studieren soll, um das herauszufinden? Vielleicht in Deutschland?
***
Übungsaufgabe
Finde die kleinste Lösung nach Lilas Schema!
Lösung