Maschinelles Lernen und Kontinuumshypothese

Ben und Rike haben eine Einladung zur Vorstellung an einem neuen KI-Institut bei Berlin erhalten. Zusammen machen sie sich auf den Weg. Als sie im ICE nach Berlin sitzen, holt Ben ein Paper von Ben-David und Kollegen 'raus und erzählt Rike von der letzten großen KI-Veröffentlichung.

Ben Hier ist was ganz Großes entdeckt worden, das müssen wir bis Berlin verstanden haben: „Die Lernfähigkeit kann unentscheidbar sein.“

Rike Was meinst Du? Ich habe keinen Schimmer, wovon Du sprichst.

Ben Schau mal, es gibt sehr viele KI-Aufgaben von der Sorte: Mustererkennung, Regressionsanalyse, Clusterbildung, Verstehen von Sprache, Erkennen von Spam. Die werden mit Hilfe von Wahrscheinlichkeitstheorie behandelt, das ist das PAC Learning (probably approximately correct learning) oder auch die Vapnik-Chervonenkis-Theorie.

Rike Kannst Du mir mal ein konkretes Beispiel geben, das ist mir jetzt zu weit.

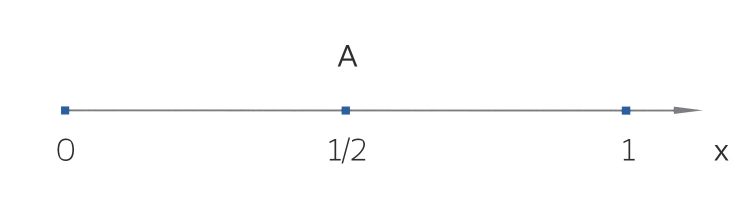
Ben Okay. Stell Dir vor, Du betreust eine Website, einen Blog, der durch Werbung finanziert wird. Der Eigentümer möchte, dass Du aus einem gegebenen Pool von „Werbung“ diejenige  platzierst, dass die mögliche Zielgruppe für die Werbung möglichst oft die Seite besucht.

Rike Hm

Ben Das Problem ist, dass man wirklich nicht weiß, welche Besucher die Seite besuchen.

Rike Kann man das Problem formalisieren?

Estimating Maximum Problem (EMX)

Ben Ja, hier: es heißt Estimating Maximum Problem (EMX):

• ist eine Menge, zB die potentielle Menge der Besucher der Website.
• ist die Menge aller Teilmengen in X, zB die Leute, die die Website (zu einer Zeit) besuchen
• ist eine unbekannte Wahrscheinlichkeitsverteilung auf

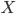
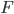
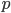
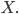
Nun ist eine Menge

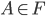
gesucht, sodass

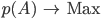
Rike Okay! Ziemlich schwierig!

Unentscheidbarkeit für EMX

Ben Ben-David und seine Kollegen können nun zeigen, dass für das folgende Problem:

• ist die Menge aller endlichen Teilmengen von X,
• ist die Menge aller Wahrscheinlichkeitsverteilungen auf mit endlichem Träger

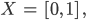
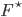
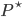
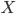
"die EMX-Lernfähigkeit dieses Systems unabhängig von den ZFC-Axiomen ist."

Hm, ziemlich knapp formuliert, kennst Du diese ZFC-Axiome?

Rike Hm, das ist die Zermelo-Fraenkel-Axiomatik (ZF), die Axiomatik für Mengen. Es gibt ein Axiom, das ist mit dem "C" gemeint, die Kontinuumshypothese, die man positiv oder negativ entscheiden kann. Je, nachdem, was Du wählst, Es entstehen 2 unabhängige Modelle. Außerdem gibt es noch das Auswahlaxiom, da geht es darum, aus einer (meistens unendlich großen Menge von Zahlen) eine Zahl auszuwählen. Auch hier kannst Du Dich für oder gegen das Axiom entscheiden.

Ben Moment mal. Also aus einer endlichen Menge von Zahlen kann ich immer eine auswählen, ich würde die erste nehmen, sag ich mal so – als Informatiker. Bei einer unendlichen Menge ist das schwieriger. Okay, wenn ich dauernd Daten reinkriege und schon immer welche da waren, unsortiert, dann habe ich ein Problem, ein Programm zu schreiben, um ein Zahl auszuwählen, okay. Ziemlich cool. Wer hat sowas bewiesen?

Rike Das hat Paul Cohen 1963 gezeigt. Und Gödel hat gezeigt, dass man nicht innerhalb der Zermelo-Fraenkel-Axiomatik (ZF) die Unabhängigkeit der Kontinuumshypothese und des Auswahlaxioms zeigen kann.

Ben Wie geht das mit der Kontinuumshypothese? Kennst Du Dich da aus aus?

Kontinuumshypothese

Rike Ich versuch‘ mal, es Dir zu erklären.

Potenzmengen P

Rike Okay, lass uns mal eine Menge 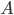aus 3 Zahlen nehmen:

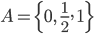
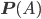
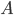
Die Potenzmenge besteht aus allen Teilmengen von :
das sind:

die leere Menge,



ist die letzte Untermenge.

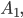
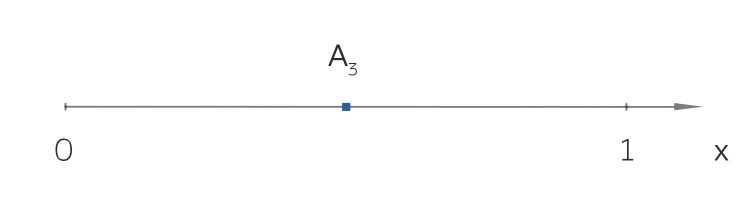
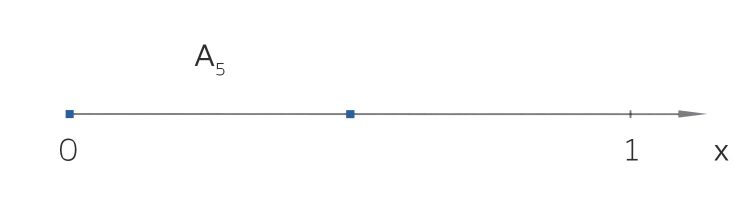
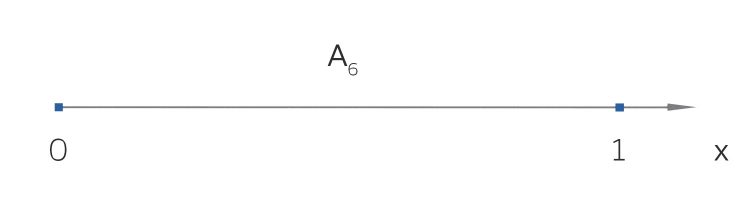
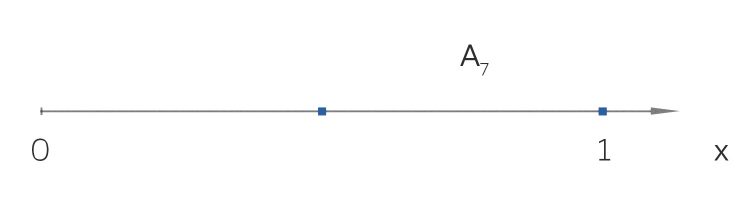
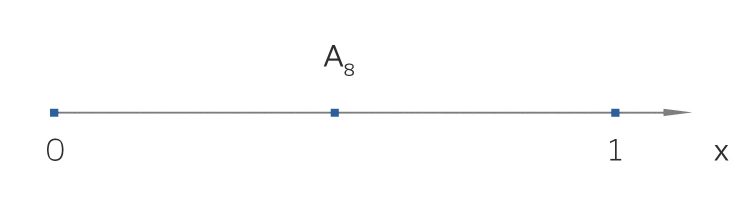
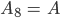
Ben Hey, Rike, aus 3 macht 8!

Rike Stimmt, die Anzahl der Elemente der Potenzmenge kann man gut berechnen:

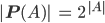
Man kann diese 2er Potenz auch gut darstellen, nur mal so, damit Du die Dimension siehst:

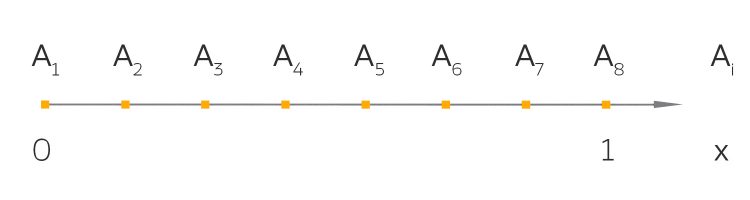
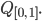
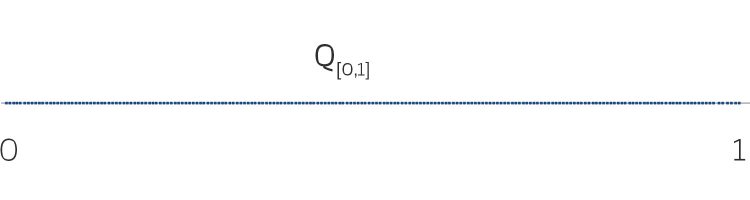
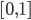Jetzt lass uns die rationalen Zahlen zwischen 0 und 1 nehmen: Das sind unendlich abzählbar viele.

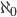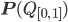
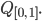
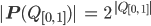
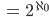
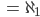
Ihre Kardinalzahl oder Mächtigkeit heißt . Wenn wir nun alle möglichen Teilmengen daraus bilden, ist das die Potenzmenge von Jetzt rechnen wir wieder die Anzahl aus und kriegen ganz formal:

Ben Ganz formal?

Rike Naja, die Größenordnung der Potenzmenge aller Brüche zwischen 0 und 1 ist echt größer als die Anzahl der Brüche selbst. Dafür hat Cantor dieses Symbol 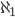geschaffen. Er hat es auch bewiesen, dass diese Potenzmenge nicht mehr abzählbar ist.

Ben Dann ist ja alles klar!

Rike Nein, es ist noch nicht klar, ob diese vielen Teilmengen von 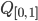ein Kontinuum bilden – oder ob das "überüberabzählbar" viele sind.

Ben Verstehe, jetzt können wir mit dem EMX-Problem weitermachen.

Der Beweis geht so:

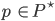
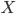
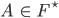
Sie müssen für ein und (gleich und unabhängig verteilte) Punkte in eine endliche Menge

finden, sodass

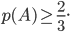
Wenn die Kontinuumshypothese – die ich jetzt kenne – wahr ist, dann kann man so ein 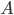finden, wenn nicht, dann nicht. Also ist diese Konstellation unentscheidbar.

Fazit

Rike

Folglich kann man selbst zwischen den Modellen wählen:

Modell 1 mit 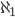ist die Mächtigkeit des Kontinuums
Modell 2 mit 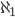ist kleiner als die Mächtigkeit des Kontinuums

Und so ist das wohl hier auch.

Ben Ja, wenn wir im ersten Modell sind, dann bleibt noch die konstruktive Aufgabe zu lösen, die Menge A der Werbung bzw. der Besucher wirklich zu finden; wenn wir im 2. Modell sind, ist die Aufgabe prinzipiell nicht lösbar. Solange stochern alle nur im Nebel, verteilen Werbung mit der Gießkanne!

Aber Rike, sind das großartige Herausforderungen? Es geht darum, Lernbarkeit nicht schnell zu implementieren, sondern prinzipiell zu durchdenken, Modelle zu kreieren und später den Aufwand abzuschätzen.

Rike Ja, das gefällt mir.

***

Übungsaufgabe

Beweise

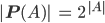
für !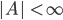

Lösung

Mit vollständiger Induktion über 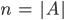.