Lila verbringt ein paar Tage bei ihrer Freundin Maya in Mandarmani, am Meer. Dort sind die beiden oft am Strand. Lila diskutiert mit Maya, ob sie wohl Mathe oder Informatik in Deutschland studieren sollte. Aber was liegt ihr mehr? Sie hat bis jetzt ein kleines Programm zur Suche von Mersenne-Primzahlen ausgeführt und verstanden, doch was muss man wirklich lernen? Kann sie Informatik lernen? Kann sie es systematisch erlernen? Oder verbringt man einfach sehr viel Zeit mit dem Rechner? Was ist das Wesen von Informatik?
Schließlich empfiehlt ihr Maya das Buch von Donald Knuth: The Art of Computer Programming. Hier wird viel von Zahlen, vollständiger Induktion und Sortieren gesprochen. Am Beispiel des größten gemeinsamen Teilers zweier Zahlen bekommt sie eine Ahnung von der Kunst des Programmierens.
Maya Wenn man zwei natürliche Zahlen 
und 
hat, dann ist deren größten gemeinsamen Teiler gesucht. Das ist die Einstiegsaufgabe.
Lila Hm, wenn ich von jeder dieser beiden Zahlen die Teiler wüsste, könnte ich den größten gemeinsamen leicht raussuchen. Aber wie finde ich die Teiler? Soll ich alle Zahlen, die kleiner als und sind, ausprobieren?
Euklidischer Algorithmus
Maya Nein, schau mal, das dauert bei großen Zahlen zu lange, das ist nicht effizient. Donald Knuth schlägt den euklidischen Algorithmus vor. Der geht so:
- Du nimmst die beiden Zahlen und und dividierst sie durcheinander: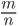
. - Ist das ohne Rest möglich, dann teilt die Zahl . ist der größte gemeinsame Teiler.
- Bleibt ein Rest
, dann ersetzt Du m durch und durch . Und fängst wieder beim 2. Punkt an.
Beispiel
Lila Ich durchschaue es nicht. Ich rechne mal ein Beispiel. Gut, nehmen wir seins:
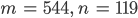
Dann kriege ich
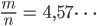
Zur Berechnung des Restes brauche ich nur den ganzen Anteil von 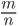, das ist dann 4, so gehts weiter:
Okay,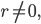 
dann ist jetzt
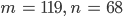
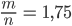
Das ergibt für den Rest
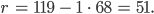
Der Rest ist ungleich Null, dann
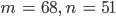
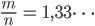
Für den Rest kriege ich
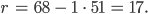
Weiter,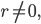
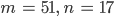
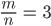
Da gibt es keinen Rest, dann hast Du gesagt….
Maya teilt , ist der größte gemeinsame Teiler.
Lila Gut. 17 ist der größte gemeinsame Teiler von 544 und 119. Stimmt. Ich wäre nie auf diesen Algorithmus gekommen. Wie funktioniert der?
Endlichkeit des Algorithmus
Maya Hier, Du hast gerechnet:
| Schritt | m | n | r |
| 1 | 544 | 119 | 68 |
| 2 | 119 | 68 | 51 |
| 3 | 68 | 51 | 17 |
| 4 | 51 | 17 | 0 |
Dabei hast Du intuitiv die Definition des Restes benutzt:
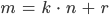
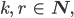
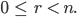
Das ist immer kleiner als , das ist wichtig. Auf diese Weise wird die Folge der Reste immer kleiner und muss bei Null enden.
Korrektheit des Algorithmus
Lila Cool! Aber wieso kommt die richtige Zahl raus?
Maya Wenn beim ersten Schritt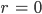 
ist, dann teilt die Zahl . Das ist natürlich bei jedem Schritt so. Wenn 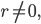dann ist
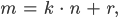
wieder mit natürlichen 
und , 
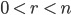
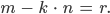
Jede Zahl, die und teilt, muss auch teilen. Das ist so ein typisch algebraisches Argument, das sind gleiche Eigenschaften der Ausdrücke rechts und links vom Gleichheitszeichen.
Lila Gut, verstehe.
Maya Und für jede größte Zahl von Teilern gilt das auch. Also können wir statt der Aufgabe, den größten Teiler von und zu suchen, die Aufgabe lösen, den größten Teiler von und zu suchen.
Lila Verstehe. Ziemlich intelligent. Jetzt versuche ich mal, das zu programmieren. Hast Du ein schönes Beispiel für mich?
Maya Na, 2 166 und 6 099! Viel Spaß!
Lila Dann versuch ich‘s mal!
***
Übungsaufgaben
- Löse Mayas Aufgabe!
- Finde den größten gemeinsamen Teiler von 2 167 und 7 000.
- Finde den größten gemeinsamen Teiler von 971 230 541 und
2 964 081. - Was ist, wenn
?
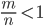Lösungen
- ggT(2 166, 6 099) = 57
- ggT(2 167, 7 000) = 1
- ggT(971 230 541, 2 964 081) = 988 027
- Dann tausche die Zahlen und .