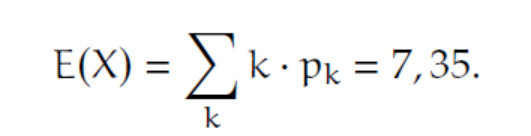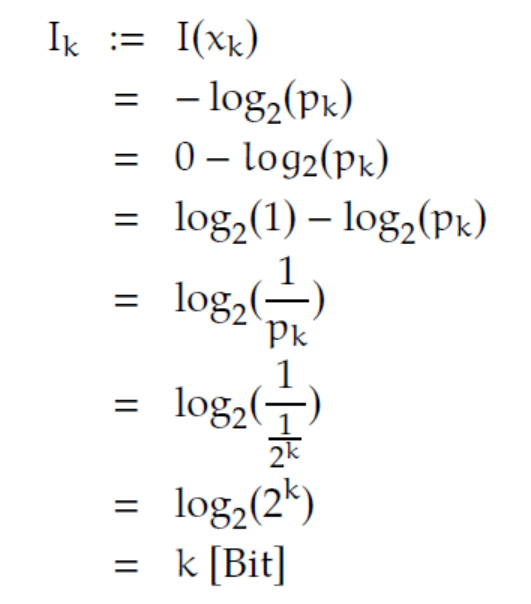Rike und Ben sind in Berlin angekommen. In ihrem Institut für KI gibt es flache Hierarchien, nicht so wie an der Uni, wo ein „weiser“ Prof. die Themen bestimmt. Jetzt erarbeiten sich alle das Wissen zusammen und tauschen sich darüber aus.
Sie fangen mit Text an und fragen, ob ein Text einen Informationsgehalt hat. Das ist schwer zu beantworten, man muss es auf Wörter und Buchstaben herunterbrechen. Rike soll einen kleinen Vortrag darüber halten. Sie sucht viele Bücher über Information in Texten zusammen, sie vergisst ihre Umgebung, gedankenverloren sitzt sie inmittten eines unaufgeräumten Bücherstapels bis Ben kommt und ihr hilft.
Ben Hi, Rike, ist alles okay?
Rike Ben, ich finde mein Thema echt schwierig. Informationsgehalt von Texten! Ich finde schon den Informationsbegriff so schwierig, viel schwieriger als eine Wahrscheinlichkeitsverteilung. Bei Wiki finde ich die Häufigkeitsverteilung von den einzelnen Buchstaben in deutschen Texten, das prüfe ich jetzt erst mal nach.
Ben Gut!
Buchstabenhäufigkeiten in "Effi Briest"
Rike Da habe ich mir den Effi-Briest-Text genommen und die folgenden Häufigkeiten gefunden:
| Buchstabe | Abs. Häufigkeit | Rel. Häufigkeit pk | Rang  |
| e | 73 640 | 0,1570 | 1 |
| n | 48 371 | 0,1031 | 2 |
| i | 39 250 | 0,0837 | 3 |
| r | 30 303 | 0,0646 | 4 |
| s | 30 112 | 0,0642 | 5 |
| a | 29 566 | 0,0630 | 6 |
| h | 26 767 | 0,0571 | 7 |
| t | 26 740 | 0,0570 | 8 |
| d | 23 432 | 0,0500 | 9 |
| u | 17 671 | 0,0377 | 10 |
| c | 17 026 | 0,0363 | 11 |
| l | 16 621 | 0,0354 | 12 |
| g | 13 124 | 0,0280 | 13 |
| m | 12 570 | 0,0268 | 14 |
| o | 11 296 | 0,0241 | 15 |
| w | 9 299 | 0,0198 | 16 |
| b | 9 288 | 0,0198 | 17 |
| f | 7 642 | 0,0163 | 18 |
| k | 5 480 | 0,0117 | 19 |
| z | 4 732 | 0,0101 | 20 |
| v | 3 361 | 0,0072 | 21 |
| ü | 3 149 | 0,0067 | 22 |
| p | 2 633 | 0,0056 | 23 |
| ä | 2 240 | 0,0048 | 24 |
| ß | 2 216 | 0,0047 | 25 |
| j | 1 265 | 0,0027 | 26 |
| ö | 992 | 0,0021 | 27 |
| y | 79 | 0,0002 | 28 |
| q | 76 | 0,0002 | 29 |
| x | 35 | 0,0001 | 30 |
Tabelle der Buchstabenhäufigkeiten im Roman „Effi Briest“ von Th. Fontane.
Da kann ich gut die relative Häufigkeit ausrechnen (bei insgesamt 468 976 vorkommenden Buchstaben). Ich habe zu jedem Buchstaben den „Rang“ eingeführt, eine Art Sortierung. pk ist die Wahrscheinlichkeit, dass der -te Buchstabe im Text vorkommt, das ist gerade die relative Häufigkeit.
Ben Gut.
Rike Zu jedem Buchstaben kann ich einen Erwartungswert E(xk) ausrechnen,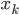 
ist das Ereignis, den Buchstaben bei einer Auswahl eines Buchstabens aus dem Text anzutreffen:
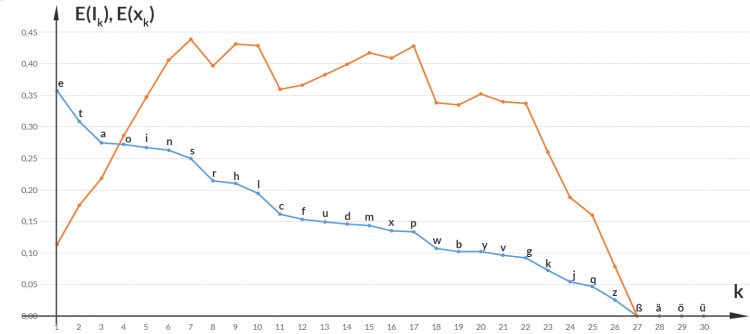
Da hat der 8. Buchstabe, das "t", den größten Wert. Das kann ich auch mitteln über alle Buchstaben und erhalte den Erwartungswert der Zufallsgröße 
die die Buchstabenverteilung im Text beschreibt.
Das ergibt hier:
Das bedeutet, dass ich im Mittel den 7. Buchstaben antreffe, das "h". Bei einer Gleichverteilung oder bei einer zentrierten Normalverteilung wäre das der 15. (von 30) Buchstaben, das "o".
Aber was liefert mir die Shannon-Formel?
Die Shannon-Formel für den Informationsgehalt
Ben Die Shannon-Formel
beschreibt den Informationgehalt des Ereignisses xk, das sieht so aus:
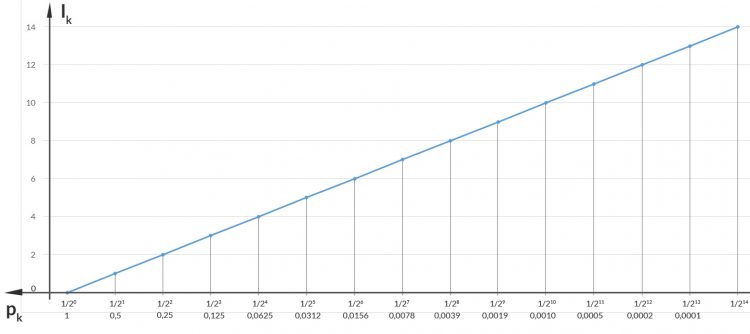
Löse Dich mal vom konkreten Text und denke mal wie ein Informatiker, wie in guten alten Zeiten mit der Turingmaschine und so.
Rike Hm. Cooles Diagramm, nach rechts werden die Zahlen immer kleiner!
Die Shannon-Formel für spezielle Häufigkeiten
Ben Hättest Du mir gar nicht zugetraut! Nehmen wir mal an, wir haben ein Ereignis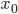 
mit Wahrscheinlichkeit
Dann hat das Eintreten des Ereignisses keine Information, es ist „sicher“, sagen die Mathematiker. Shannon sagt,
Rike Gut.
Ben Weiter, nehmen wir
Dann berechnen wir
Rike Na gut! Was ist das mit dem “Bit”?
Ben Das ist eine Pseudoeinheit für die Anzahl der Stellen in Binärdarstellung, aber das will ich Dir gerade erklären. Allgemein nimmt man die Logarithmengesetze und kommt für
auf:
Verstehst Du Rike, der Informationsgehalt für ein Ereignis mit Wahrscheinlichkeit 2-k ist 
Informationsgehalt einzelner Buchstaben bei "Effi Briest"
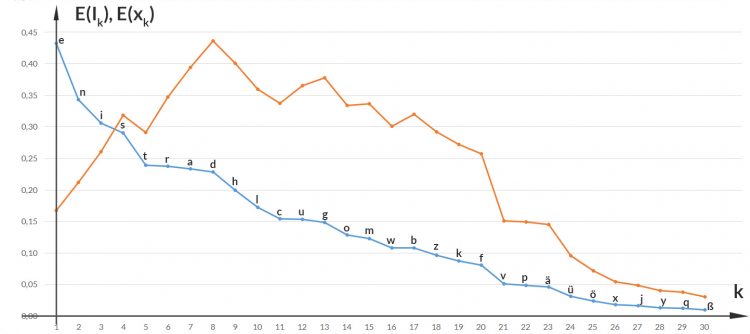
Rike Okay, das ist die Anzahl der Stellen, die die Turingmaschine braucht, um 2-k binär zu schreiben, Deine Bits. Toll! Verstehe! Die Buchstaben mit kleinerer Häufigkeit haben die größere Information. Warte, jetzt rechne ich das aus:
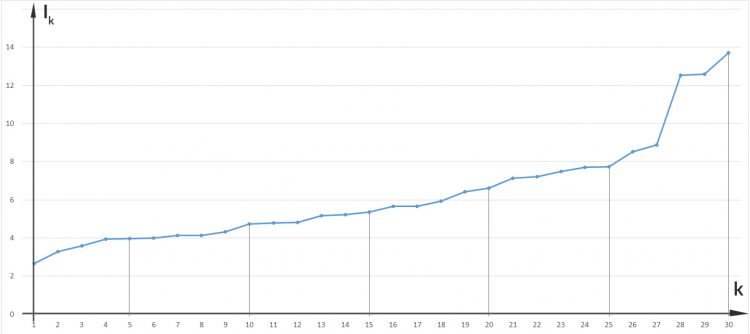
Ben Richtig. Jetzt kannst Du noch den Erwartungswert der Information für jeden Buchstaben ausrechen:
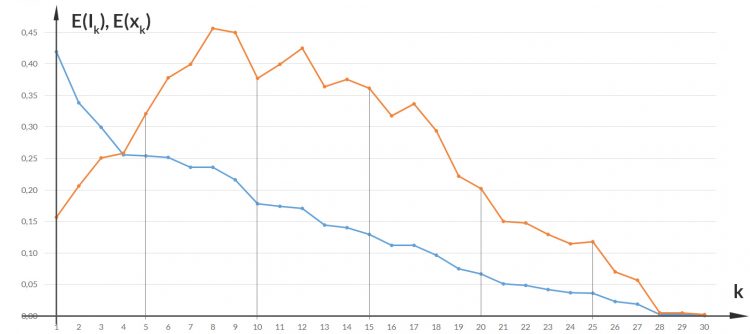
Ben Dann kannst Du natürlich auch den Erwartungswert der Information insgesamt berechnen, was gibt das denn?
Mittlerer Informationsgehalt
Rike Warte!
Ben Schön, im Mittel haben wir einen Informationsgehalt von 4. Das ist nicht viel, das hat Fontane gut gemacht!
***
Übungsaufgabe
Berechne E(I) und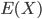 
für einen anderen digital verfügbaren Text.
Lösung
