Lila hat geträumt, dass sie beim Programmieren des euklidischen Algorithmus aus der Schleife mit der Abfrage niemals herauskommt. Was soll sie tun? Das Programm rechnet und rechnet und hört nie auf. Sie hat das Gefühl, dass sie die Geister, die sie rief, niemals loswerden kann. Sie kommen, verrichten Unheil, vermehren sich und sind nicht zu stoppen. Kann ein Programm eine Seele haben? Kann eine Maschine ein Bewusstsein haben? Beim Frühstück mit ihrer Freundin Maya bekommt sie keinen Bissen runter.
Der Zauberlehrling-Traum vom euklidischen Algorithmus
Maya Hi Lila, was ist denn passiert?
Lila Ich habe geträumt, beim Euklidischen Algorithmus nicht aus der Schleife herauszukommen. Es war so schrecklich…
Maya Hm. Wollen wir den Algorithmus nochmal durchgehen?
Lila Ja, gut. Also, ich habe zwei Zahlen m und n. Ich teile  durch
durch  und berechne den Rest. Ist der Rest Null, dann bin ich fertig,
und berechne den Rest. Ist der Rest Null, dann bin ich fertig,  ist der größte gemeinsame Teiler. Ist der Rest nicht Null, muss ich
ist der größte gemeinsame Teiler. Ist der Rest nicht Null, muss ich  durch
durch  ersetzen und
ersetzen und  durch
durch 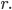 Dann fange ich wieder von vorn an.
Dann fange ich wieder von vorn an.
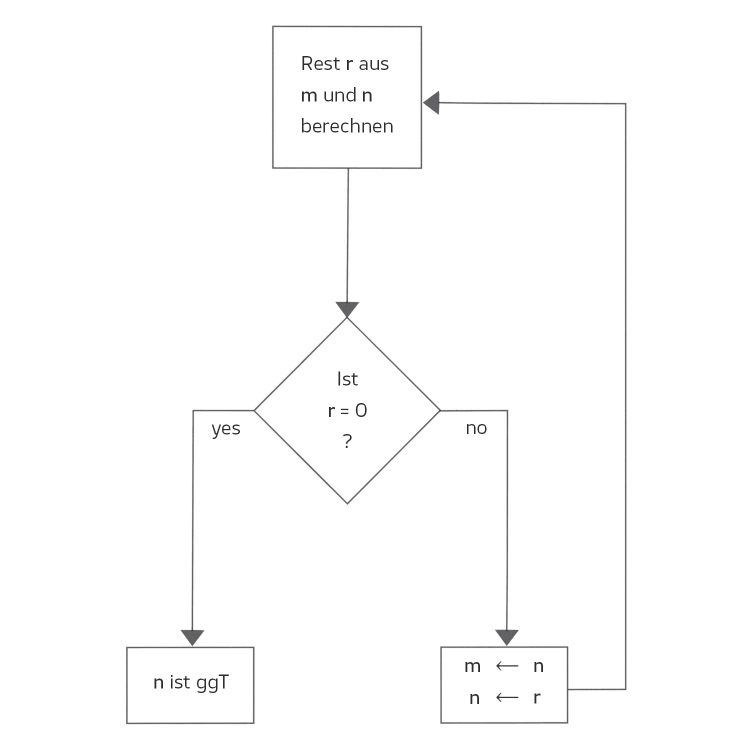
Maya Richtig. Es gibt viele Fehlerquellen darin, gut, dass wir das besprechen. Du könntest zum Beispiel den Rest  so berechnen:
so berechnen:
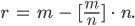
Die eckige Klammer steht dann für den ganzen Anteil einer reellen Zahl  :
: 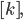 das kann man mathematisch so schreiben:
das kann man mathematisch so schreiben:
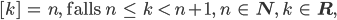
also wenn  zwischen den ganzen Zahlen
zwischen den ganzen Zahlen  und
und 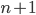 liegt, dann soll
liegt, dann soll  der ganze Anteil sein.
der ganze Anteil sein.
Lila Gut. Verstehe.
Maya Wenn wir m und n positiv wählen, dann wird  immer kleiner.
immer kleiner.  ist nichtnegativ aufgrund seiner Konstruktion. Also ist die Folge der
ist nichtnegativ aufgrund seiner Konstruktion. Also ist die Folge der  ’s monoton fallend. Der euklidische Algorithmus startet mit natürlichen Zahlen,
’s monoton fallend. Der euklidische Algorithmus startet mit natürlichen Zahlen,  ist natürlich oder 0 und wird nach endlich vielen Schritte Null.
ist natürlich oder 0 und wird nach endlich vielen Schritte Null.
Lila Okay.
Ein Negativbeispiel
Maya Wenn Du nun ein Programm schreibst und  versehentlich nicht natürlich wählst, sagen wir mal:
versehentlich nicht natürlich wählst, sagen wir mal:
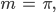
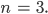
Dann kriegen wir für den ersten Rest:
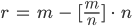
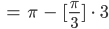
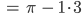
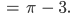
Lila Gut. Lass mich mal weiter rechnen. Dann setzen wir
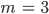
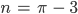
und für  erhalten wir:
erhalten wir:
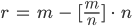
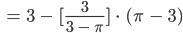
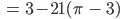
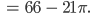
Hmm?
Maya Ja, so geht es immer weiter, für das nächste  kriegst Du eine Gleichung
kriegst Du eine Gleichung
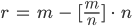
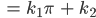
mit ganzen Koeffizienten 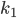 und
und 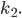
Lila Und dann? Ach ja, π ist transzendent, es löst keine algebraische Gleichung! Also wird  niemals Null! Ja, das war mein Traum!
niemals Null! Ja, das war mein Traum!
Maya Richtig,  wird immer kleiner, aber niemals Null. Du rechnest und rechnest und rechnest….
wird immer kleiner, aber niemals Null. Du rechnest und rechnest und rechnest….
Die Rettung
Lila Lass mal den Scherz. Es kann wohl nicht nur im Traum passieren, dass man aus einer Schleife nicht herauskommt.
Maya Ja, genau, Goethes Zauberlehrling! Es ist ein Klischee für fehlendes Bewusstsein für Maschinen und fehlerhaftes Programmieren. Doch man kann ernsthaft was gegen solche und andere Fehler tun. Zuerst denkst Du, kein Mensch wird je für π und 3 den größten gemeinsamen Teiler suchen, aber dann kommt jemand, um Dein Programm zu testen, und der gibt als erstes π und 3 ein….
Lila Na gut, dem kann ich ja vorbeugen, ich lasse nur natürliche Zahlen zu und teste das vor dem Eingang, als Fehlermeldung können wir ja den Zauberlehrling benutzen, haha! Jetzt muß ich mal Max fragen, ob das schon mal jemand in Deutschland gemacht hat und warum Goethe so ein schlechter Programmierer war!
***
Übungsaufgaben
- Welche Dinge müssen beim Ausführen des Algorithmus noch getestet werden?
- Kann man den Rest auch anders berechnen?
Lösungen
- Bei jeder Division muss getestet werden, ob der Nenner Null ist.
- Sind die beiden Zweige nach der Entscheidung richtig programmiert, syntaktisch und inhaltlich?
- Ist der Rest eine natürliche Zahl oder Null?
- Ist das Ergebnis eine natürliche Zahl?
- Ist das Ergebnis wirklich Teiler der Ausgangszahlen
 und
und  ?
?
- Ja, in einigen Umgeben ist die Division modulo
 als Befehl vorgesehen. Dann erhält man den Rest sofort, muss aber kontrollieren, ob die Eingangsgrößen
als Befehl vorgesehen. Dann erhält man den Rest sofort, muss aber kontrollieren, ob die Eingangsgrößen  und
und  natürliche Zahlen größer Null sind.
natürliche Zahlen größer Null sind.
