Rike, Ben und die anderen vom Institut feiern ihre erste Party. Es gibt Musik, Sekt und Bier in einem Berliner Loft. Als alle ein Glas in der Hand halten, fällt Rike die Ästhetik der aufsteigenden Blasen auf.
Rike Ist das nicht wunderschön?
Ben Ja, das ist schön, das gefällt allen theoretischen Informatikern. Nach diesem Große-Blasen-steigen-nach-oben-Phänomen wurde ein Sortieralgorithmus benannt: Bubble Sort.
Rike Erklär mal, wie der geht!
Die Bubble Sort-Idee
Ben Gut! Du fängst mit 
Zahlen an, von denen Du nicht viel weißt. Die Zahlen nennen wir mal 
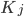und deren Anordnung oder Plätze 
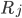. Jetzt gehst Du alle 
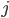Zahlen durch – von 1 bis – und prüfst, ob
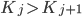
Wenn das der Fall ist, werden die Plätze getauscht
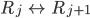
Das heißt, an der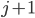 
-ten Stelle steht nun die (ehemals) 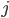-te Zahl, sie wird jetzt die 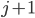-te Zahl. Hier schau Dir das am Beispiel an:
Ein Beispiel
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Kj | 49 | 08 | 51 | 06 | 90 | 17 | 89 | 27 | 65 | 42 | 15 | 50 | 61 | 67 | 76 | 70 |
16 zufällige Zahlen nach Donald Knuth
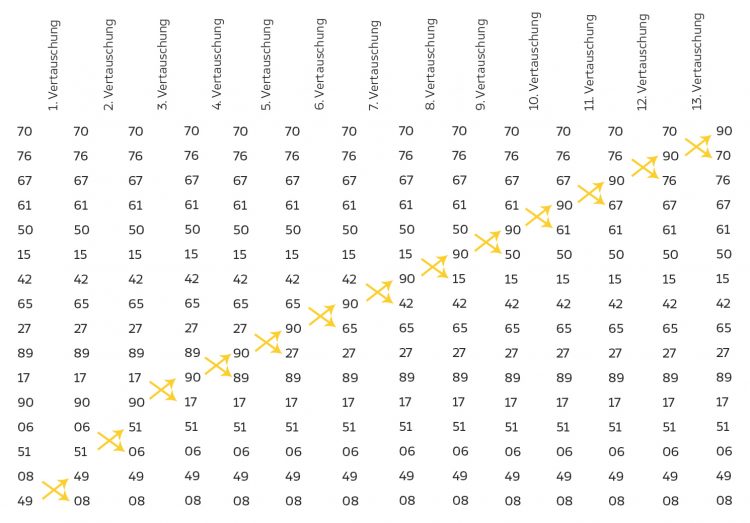
Rike Nicht schlecht, die 90 ist nach oben gerutscht! Aber Du bist noch nicht fertig!
Ben Stimmt. Du siehst, die größte Zahl hat es nach oben geschafft, das ist die Bubble-Metapher. Jetzt brauchen wir nur noch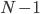 
Zahlen vergleichen. Wir fangen wieder von unten (
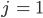) an. Im 2. Durchgang werden zuerst die 49 und die 6 getauscht, dann die 51 und die 17 und dann steigt die 89 nach oben.
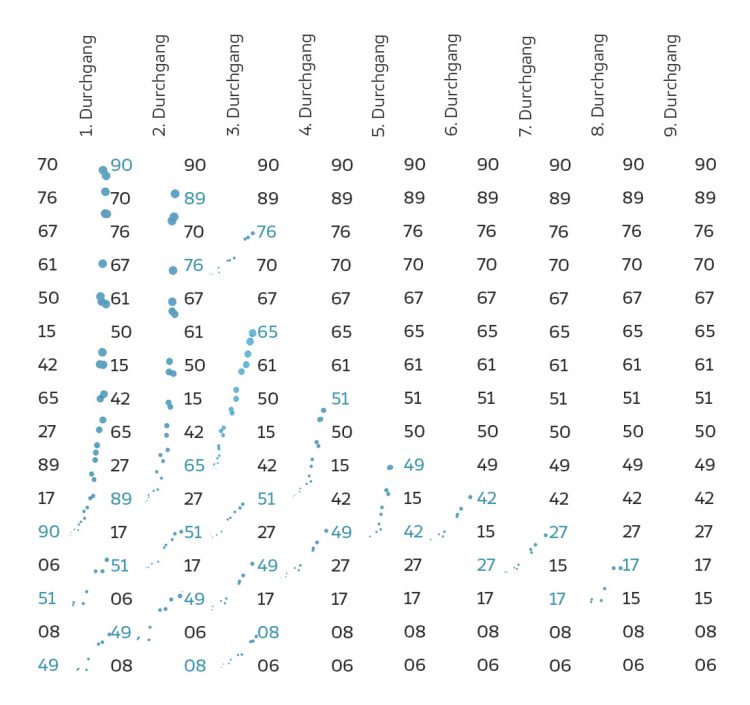
Rike Gefällt mir.
Ben Außerdem solltest Du überprüfen, ob Du fertig bist und nicht endlos die sortierte Reihe immer wieder überprüfen und endlich mal Dein Glas austrinken.
Fazit
Rike Klar, gute Idee. Sag mal, dann hast Du insgesamt höchstens solche Durchgänge und in jedem Durchgang maximal Vergleiche? Sind das nicht etwas zu viele Vergleiche,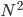 
? Du prüfst in jedem Durchlauf die unteren Zahlen erneut.
Ben Stimmt. Deshalb lieben ja nur die theoretischen Informatiker den Bubble Sort! Hahaha!
***
Übungsaufgabe
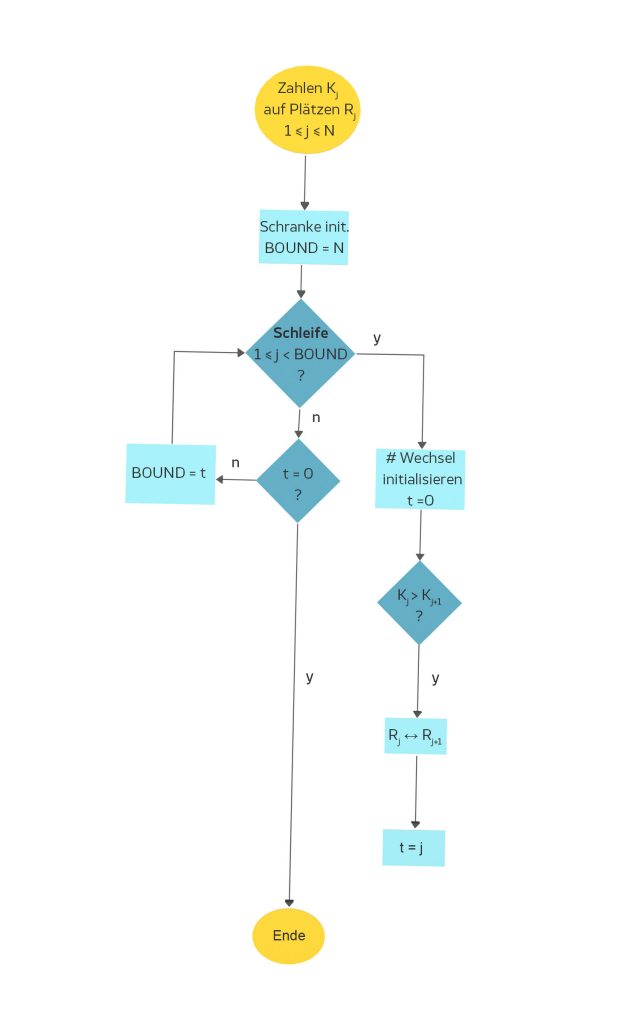
Schreibe ein Flow Chart für den Bubble Sort!
Lösung
Nach D. Knuth, aaO. S. 105.