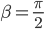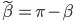Max ist an diesem regnerischen, kalten Abend zu Hause. Sein Medienproduktion-Studium hat er beendet, noch keinen Job gefunden, die deutschen Handballer haben das WM-Spiel um den 3. Platz gegen Frankreich verloren, er vermisst Lila und hätte sie gern hier. Vor lauter Verzweiflung fängt er an, sich für ihre indischen Landsleute zu interessieren. So dauert es keine 2 Minuten bis er im Netz auf Akshay Venkatesh stößt, den indisch-australischen Mathematiker, der letztes Jahr die Fields-Medaille gewonnen hat und jetzt am Institute of Advanced Studies in Princeton (USA) arbeitet. Max versteht nicht viel von den mathematischen Arbeiten, die Akshay Venkatesh veröffentlicht hat: Mordell-Vermutung, lokal symmetrische Räume, Motiv-Kohomologie, PGL2-Gruppen, Subkonvexität, hm, irgendwie findet er keinen Zugang. Doch dann entdeckt er ein Video der Simons Foundation, wo Akshay Venkatesh ein dynamisches Modell vorstellt.
Max findet, dass es wie Billard aussieht, zumindest im euklidischen Raum kennt er sich aus. Wann gibt es periodische Lösungen? Wann wird von der Spur des Balles die Dreieckfläche fast ausgefüllt? Das kann doch gar nicht so schwer sein!
Spiegeln der Dreiecke
Max malt ein paar Bilder mit den Reflexionen am Rand, doch das wird schnell unübersichtlich. So kommt ihm die Idee, die Dreiecke selbst statt die Spur zu spiegeln. Um das ursprüngliche Dreieck wieder zu erhalten, braucht er mehrere Dreiecke:
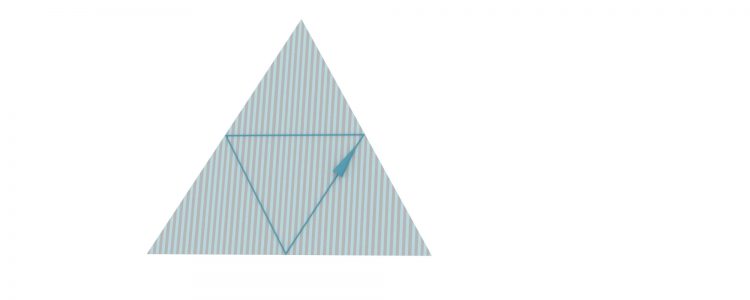
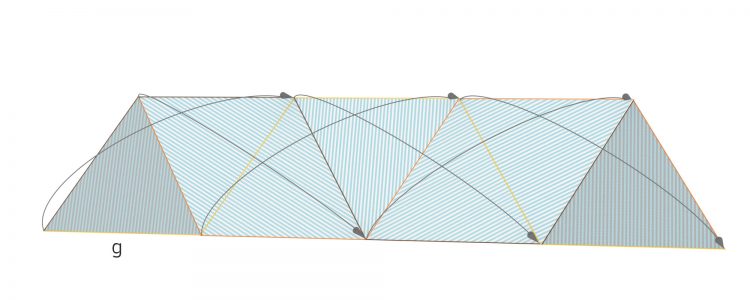Er nimmt ein gleichseitiges Dreieck mit der Seitenlänge g und spiegelt es 6 Mal. Das reicht erst mal. Jetzt zeichnet er eine Spur des Billardballes ein und beachtet das Reflexionsgesetz an der Wand:
Eigenschaften periodischer Lösungen
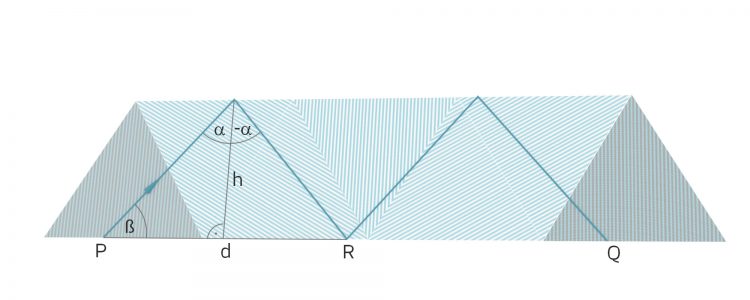Die Spur startet im Punkt P und endet im Punkt Q. Der Abstand zweier benachbarter Reflexionspunkte, hier P und R soll d sein. Na gut. Wenn nun die Punkte P und Q (im nicht gefalteten Dreieck) aufeinanderliegen sollen, dann muss die Länge der Strecke PQ ein Vielfaches von d sein:
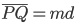
und andererseits auch ein Vielfaches der dreifachen Grundlinie.
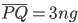
Somit hat er schon eine Gleichung:
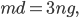
für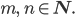 
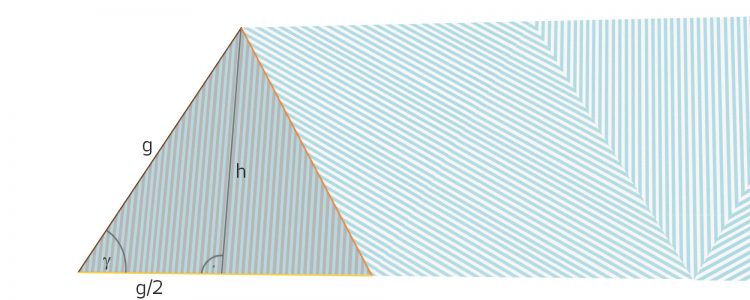
Aus dem Abstoßwinkel β,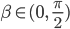 
bekommt er einen Zusammenhang von h und d:
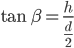
Für d benutzt er die erste Beziehung
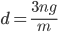
und bekommt schließlich für den Abstoßwinkel β:
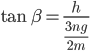
Eigenschaften des gleichseitigen Dreiecks
Er erinnert sich, dass beim gleichseitigen Dreieck die Beziehung gilt
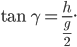
Andererseits gibt es hier ein rechtwinkliges Dreieck, für das er den Satz des Pythagoras anwendet:
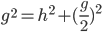
Hieraus ergibt sich
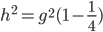
und schließlich
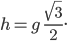
Finale Formel
Also muß der Abstoßwinkel
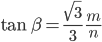
für eine periodische Lösung sein. Krass. Aber wie soll man das in der Praxis genau hinkriegen?
Sind die Ränder gekrümmt, dann funktioniert dieses Verfahren der Spiegelung und Aneinanderreihung der Dreiecke gar nicht. Da hat Akshay Venkatesh ganz andere Methoden aufgeboten, das versteht Max jetzt.
***
Übungsaufgaben
- Was passiert bei
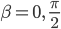oder 
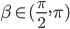? - Hat Max eine Chance, praktisch so einen Winkel zu finden?
Lösungen
- Bei β = 0 gibt es eine periodische Lösung:
Bei 
gibt es verschiedene periodische Lösungen:
Für müssen nur die Dreiecke nach links gespiegelt werden. Man setzt den Winkel
und hat das gleiche Ergebnis für
. - Ja, für β = 60° erhält man zB:
